具有变时滞的高阶模糊神经网络在有限时间内的周期间歇控制同步

蒲 浩， 蒋海军， 刘衍民

（1.遵义师范学院数学学院，贵州遵义563002；2.新疆大学数学与系统科学学院，新疆乌鲁木齐830046）

近年来，Hopfield型神经网络、联想记忆神经网络、模糊细胞神经网络、Cohen-Grossberg型神经网络等的稳定性理论和同步理论，在不同领域的实践应用和理论研究中有着广泛的应用，例如，应用在保密通信，军事领域，组合优化及人工智能系统等.为此，引起了许多研究者对不同类型的神经网络稳定性理论和同步理论的研究［1-4］.

神经网络需要在很长的时间内才能实现指数同步和指数稳定［5］.文献［5］通过 Lyapunov函数和一些不等式方法研究了具有脉冲和时滞的模糊细胞神经网络的全局指数同步，在指数同步中的

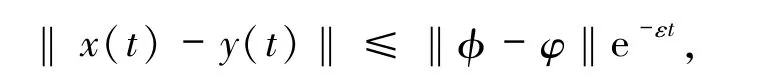
当时间t→+∞时才能实现驱动系统和响应系统的同步.然而，出于高效的考虑，在工程领域和理论研究领域需要神经网络在较短的时间内实现稳定和同步.为此，研究者对神经网络在有限时间内的同步问题进行了研究［6-7］，文献［6］在恰当的连续的反馈外部输入控制下，研究了具有时滞的Cohen-Grossberg型神经网络在有限时间内的同步.文献［7］在恰当的连续外部输入控制的条件下，通过有限时间稳定性理论研究了具有变时滞的模糊细胞神经网络在有限时间内的同步.相对于连续性输入控制同步，周期间歇输入控制是可以节约成本的一种控制方法.神经网络的周期间歇控制同步已经被广泛的进行了研究［8-9］.文献［9］不连续的周期间歇控制输入下，研究具有反应扩散项的随机模糊细胞神经网络的周期间歇指数同步.在理论研究和工程领域中，相对于一阶神经网络模型，高阶神经网络在网络容错能力、收敛速度、储存水平、逼近能力都具有较强的功能［10］.对于生物神经网络或者人工神经网络系统而言，由于系统外界干扰和系统自身因素的制约，信号在不同的神经元之间的传递过程中不可避免的会出现滞后现象，为此在神经网络系统中需要考虑时滞.然而，在过去的神经网络同步的文章中，在同一个系统中考虑通过周期间歇控制输入实现变时滞的高阶神经网络在有限时间内同步的文章甚少.

受此启发，本文通过Lyapunov函数及有限时间稳定理论等，研究具有变时滞的高阶模糊神经网络在有限时间内的周期间歇控制同步，具有较好的实用性.

1 模型和预备知识

考虑如下具有变时滞的高阶模糊神经网络模型

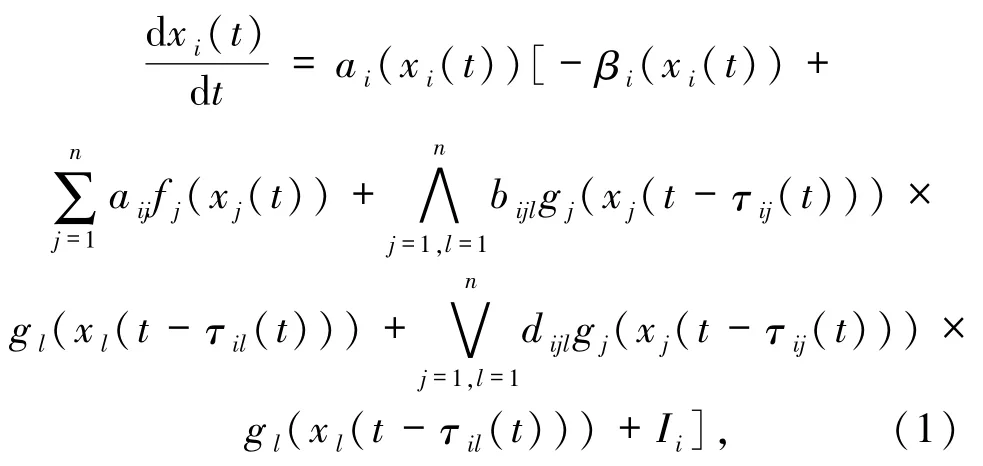
其中，1≤i≤n，xi（t）表示 t时刻第 i个神经元的状态变量，αi（xi（t））是扩大函数，βi（xi（t））是一个行为恰当函数，fj、gj是激活函数，τij（t）是信号转换时滞，且0≤τij（t）≤τ，˙τij（t）≤ρ＜1，aij表示第i个神经元和第j个神经元的连接权重系数，bij、dij分别是模糊反馈最小模板元和模糊反馈最大模板元，∧和∨分别表示模糊“和”和模糊“或”算子.

系统（1）的初值条件为

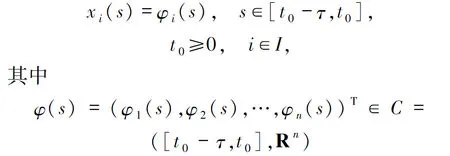
指的是把［t0-τ，t0］映射到Rn上的所有连续函数组成的一个具有p-范数的Banach空间（p≥2是一个正整数），其中p-范数在本文中定义形式为

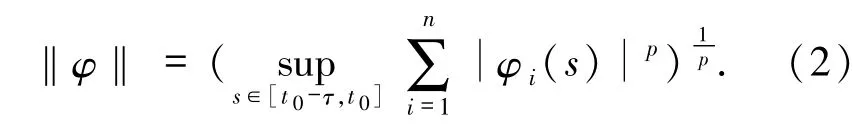
对于系统（1），假设：

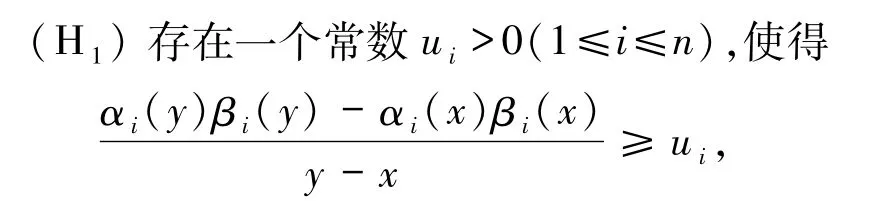
对任意的x，y∈R且x≠y成立；

对任意的 x，y∈R，1≤j≤n 成立.

把系统（1）作为主驱动系统.为了同步，引入响应系统

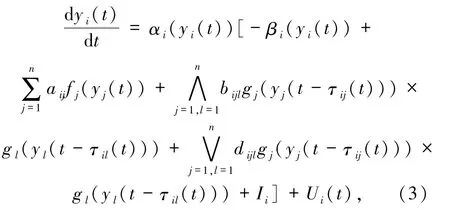
其中Ui（t）是外部周期间歇控制输入

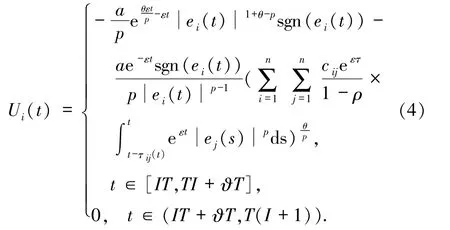
响应系统（3）的初值条件是

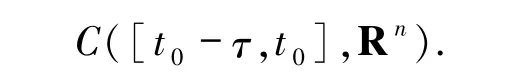
定义误差系统为

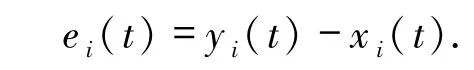
由驱动系统（1）和响应系统（3），可以得到误差系统

2 辅助引理

为了证明的需要引入下列引理.

引理1［11］假设x与y是驱动系统（1）和响应系统（3）中的2个状态变量，则下列不等式成立：

引理 2［12］（Harder） 如果 c1，c2，…，cn是正实数且0＜θ＜p，则

引理3［13］对任意的非负实数a和b，且0＜c＜1 时，不等式（a+b）c≤ac+bc成立.

引理 4［14］若函数 V（t）是当 t∈［0，+ ∞ ）时的连续非负函数，且满足

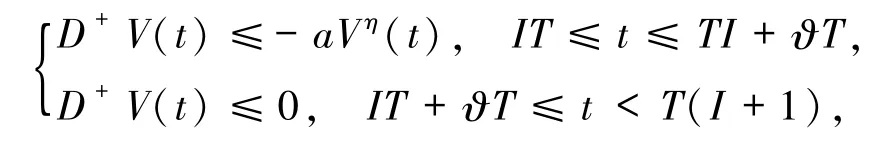
其中 a＞0，T ＞0，0 ＜η，ϑ ＜1，I∈l＝｛0，1，…，m｝是一个有限的自然数集且p是一个正整数，则有不等式

V（t）1-η≤ V（0）1-η-aϑ（1- η）t， 0 ≤ t≤ ¯T，¯T是一个有限的常数.

定义1 对于驱动系统（1）和响应系统（3），若存在一个有限的时间常数¯T≥0，使得

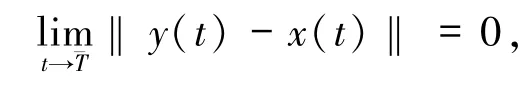
同时当 t＞ ¯T 时‖y（t）-x（t）‖ ＝0，则驱动系统（1）和响应系统（3）在有限时间（0，¯T］内同步.

3 主要结果

定理 1 如果假设（H1）～（H3）都成立，且

则驱动系统（1）和响应系统（3）在恰当的外部周期间歇控制输入 Ui（t）下，在有限时间（0，T］内是周期间歇同步的，其中

定义函数族

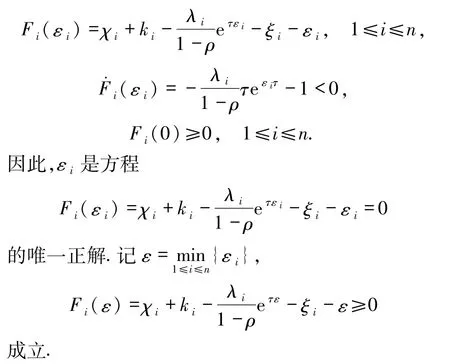
证明 构造Lyapunov函数

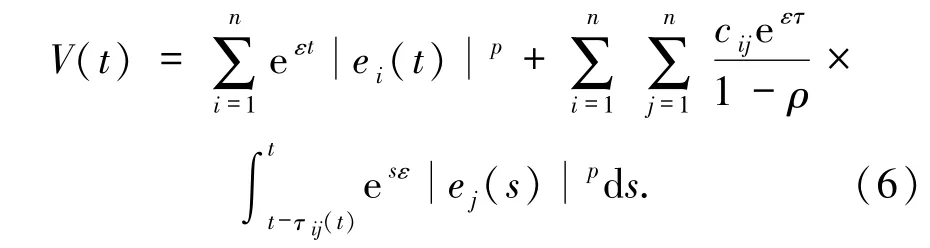
当 t∈［IT，TI+ϑT］时，结合（5）式对 V（t）关于 t计算Dini右上导数，可以得到下面的式子

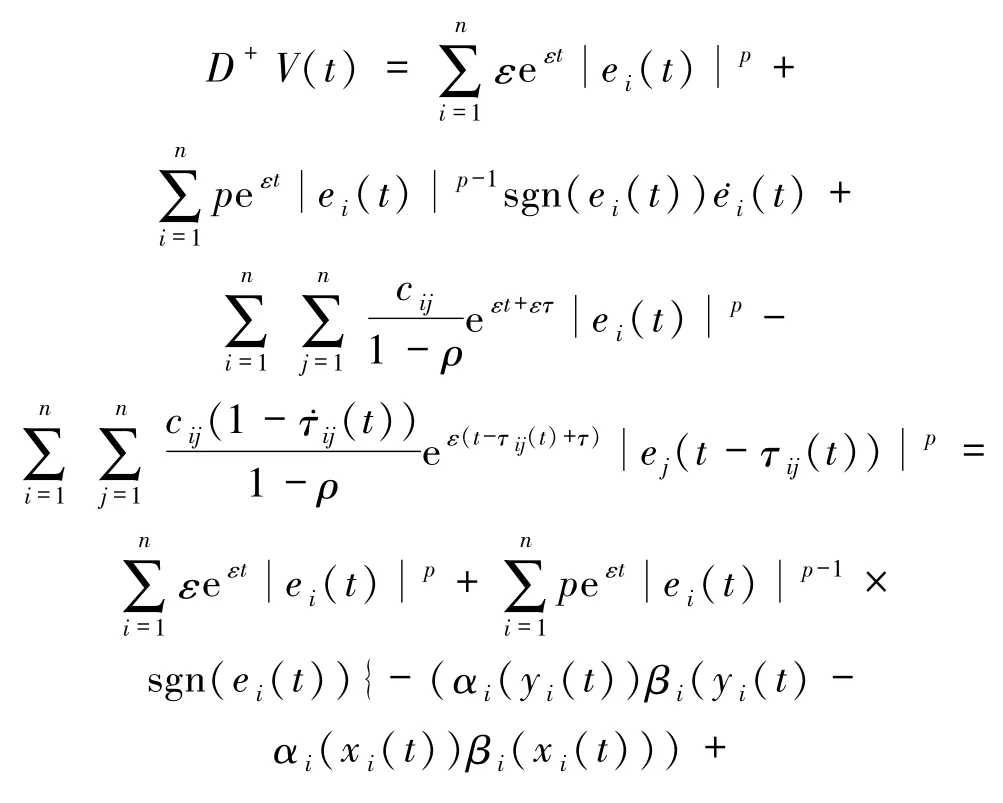
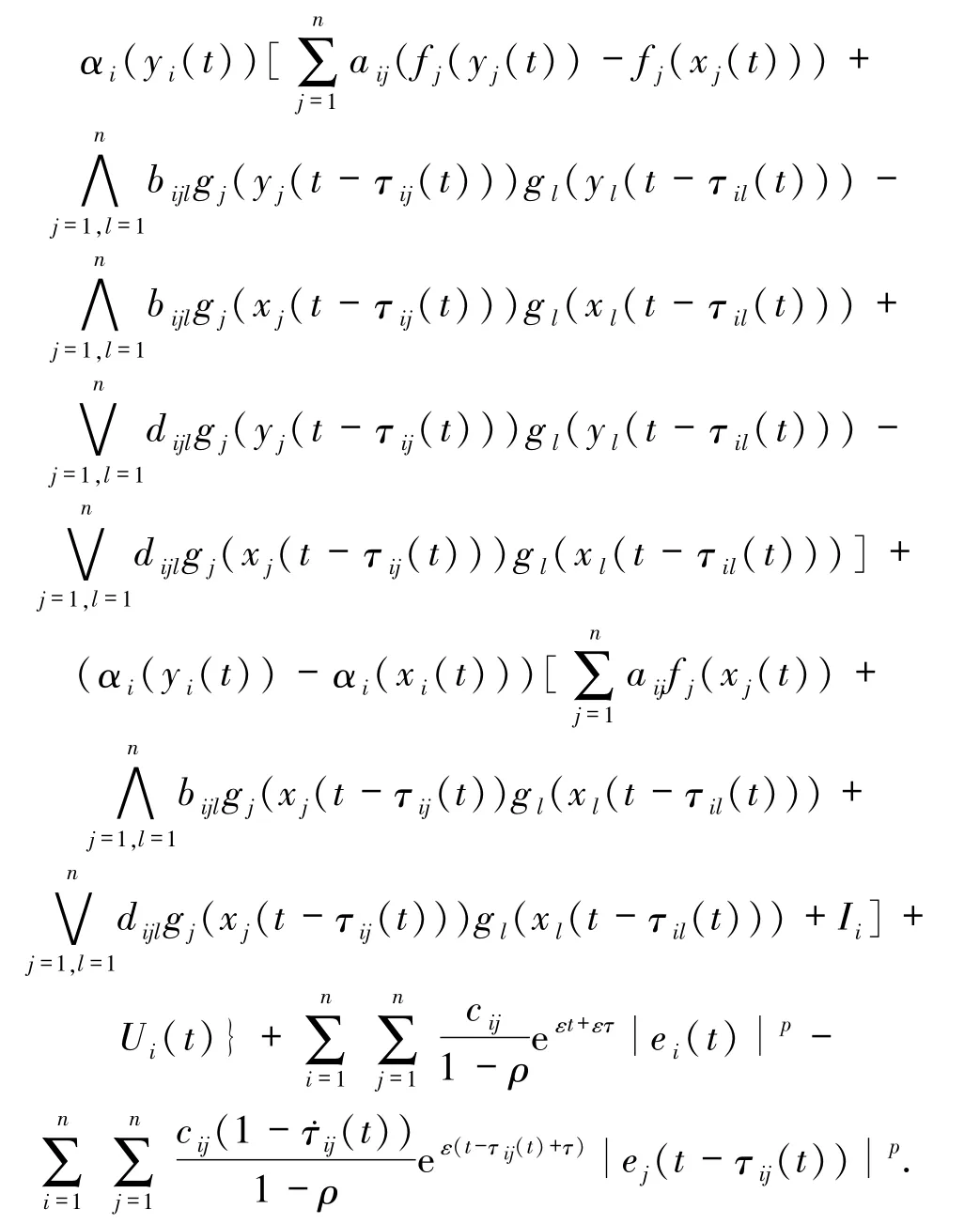
根据引理1和假设（H3）可知

结合假设（H1）和（H2）、（7）～（10）式，有

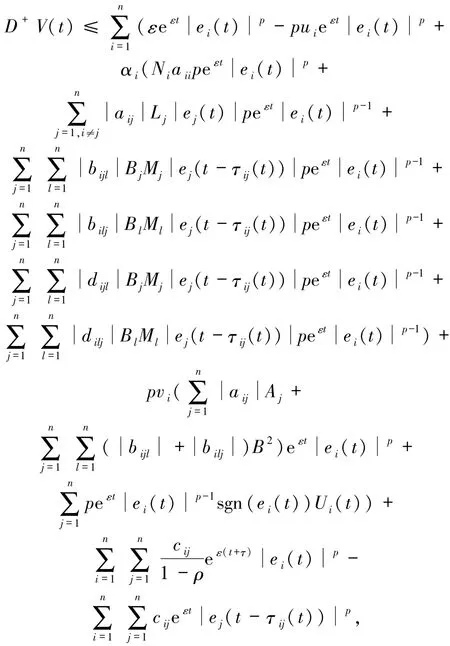
对于实数 ai＞0（1≤i≤p），有不等式

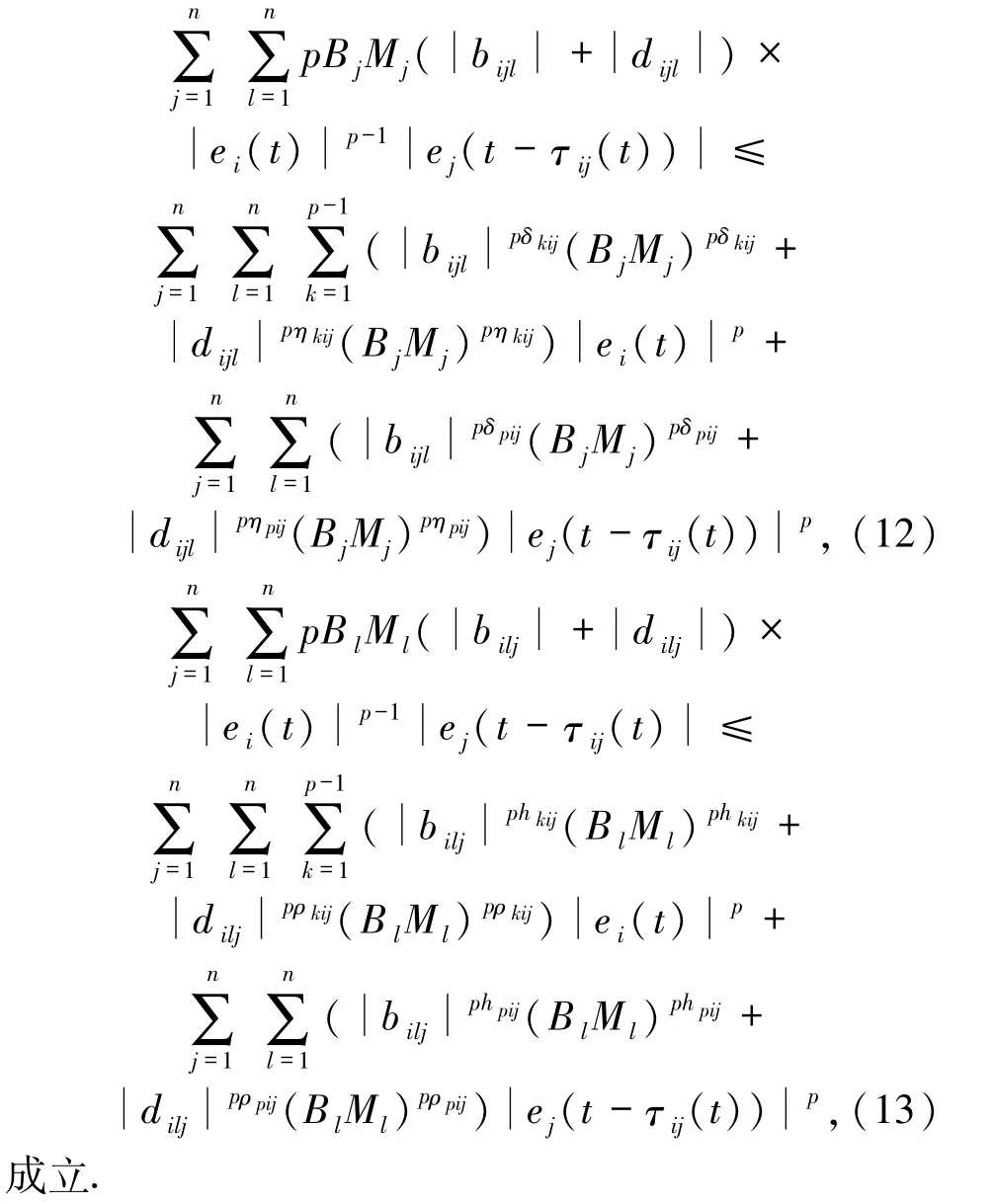
由（11）～（13）式可知

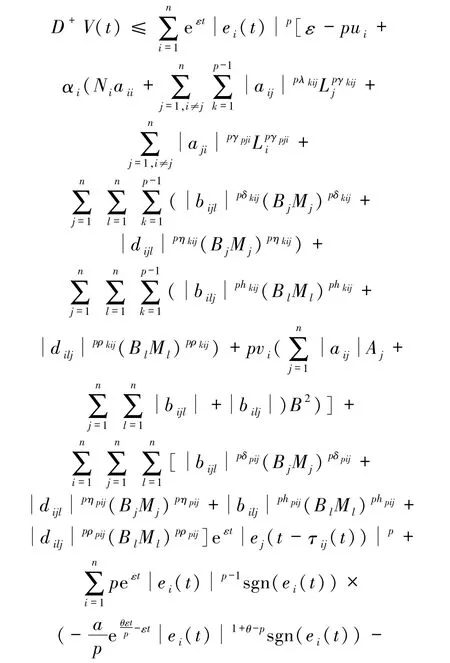
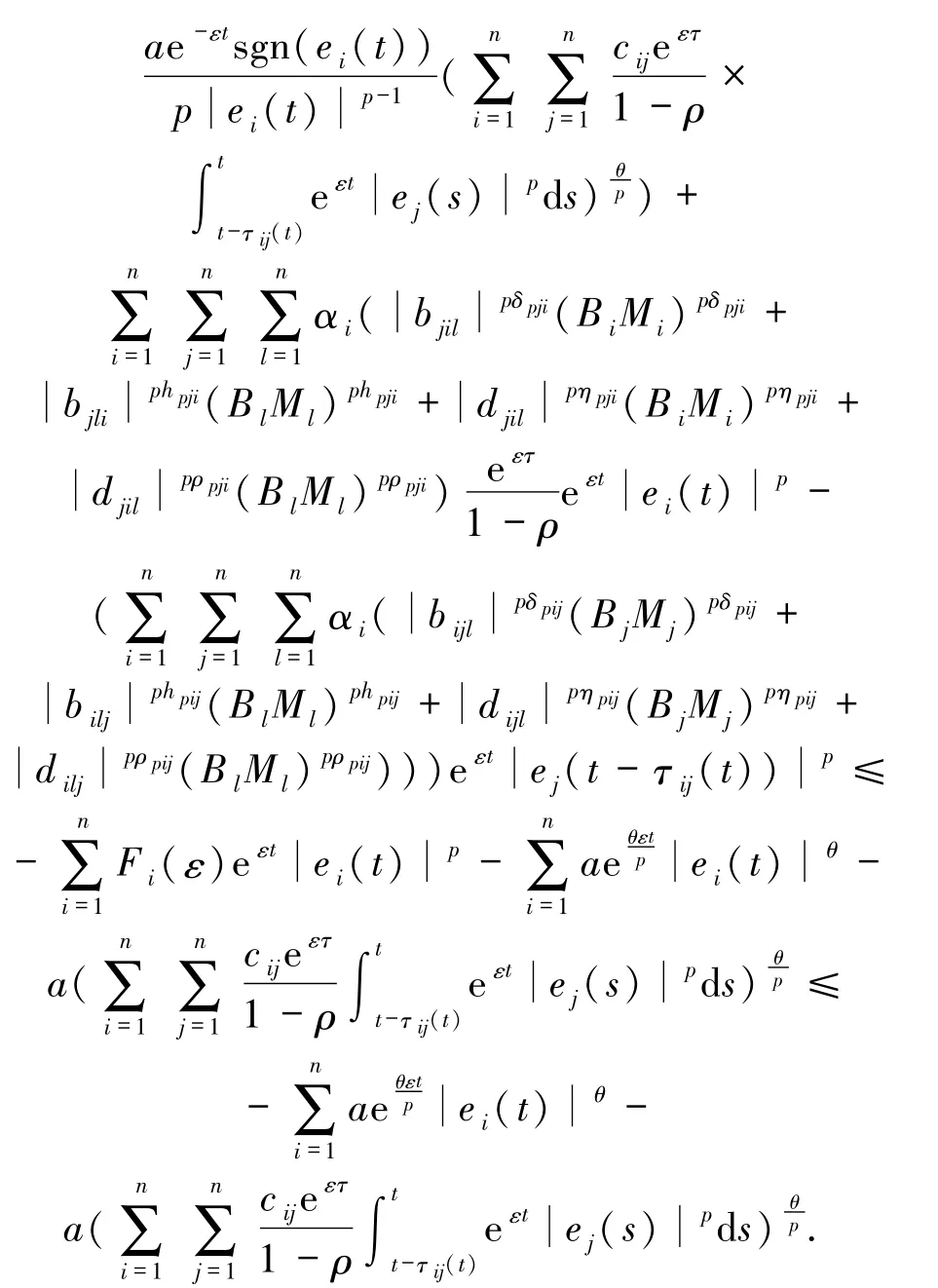
由引理2和引理3可知下列不等式

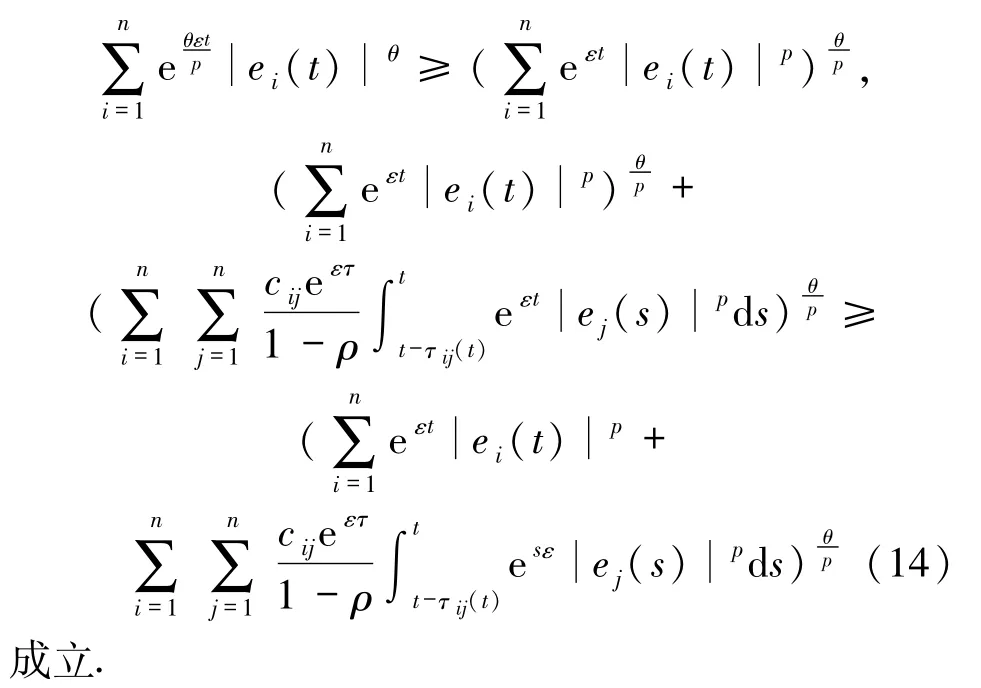
由（14）式可知

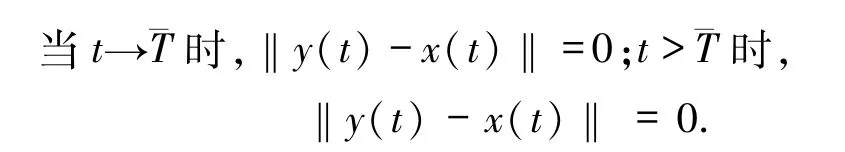
注1 在本文中所考虑的高阶模糊神经网络中，是通过恰当的外部周期间歇输入控制而不是连续性的外部输入控制，实现了在有限时间内同步而不是无限时间内同步，是对之前相关结论的推广.

注2 通过

可以发现，在周期间歇控制过程中，控制时间越长，系统实现同步的有限时间¯T越短.在实际应用中，可以适当的延长间歇控制时间就可以更快的实现系统同步.

4 推论

当 αi（xi（t））＝1 时，驱动系统（1）和响应系统（3）变为

其中Ki（t）是外部周期间歇控制输入，当

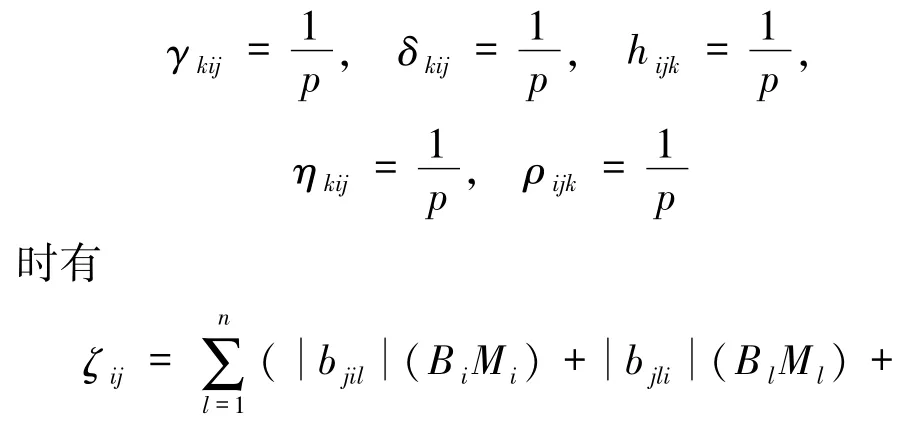
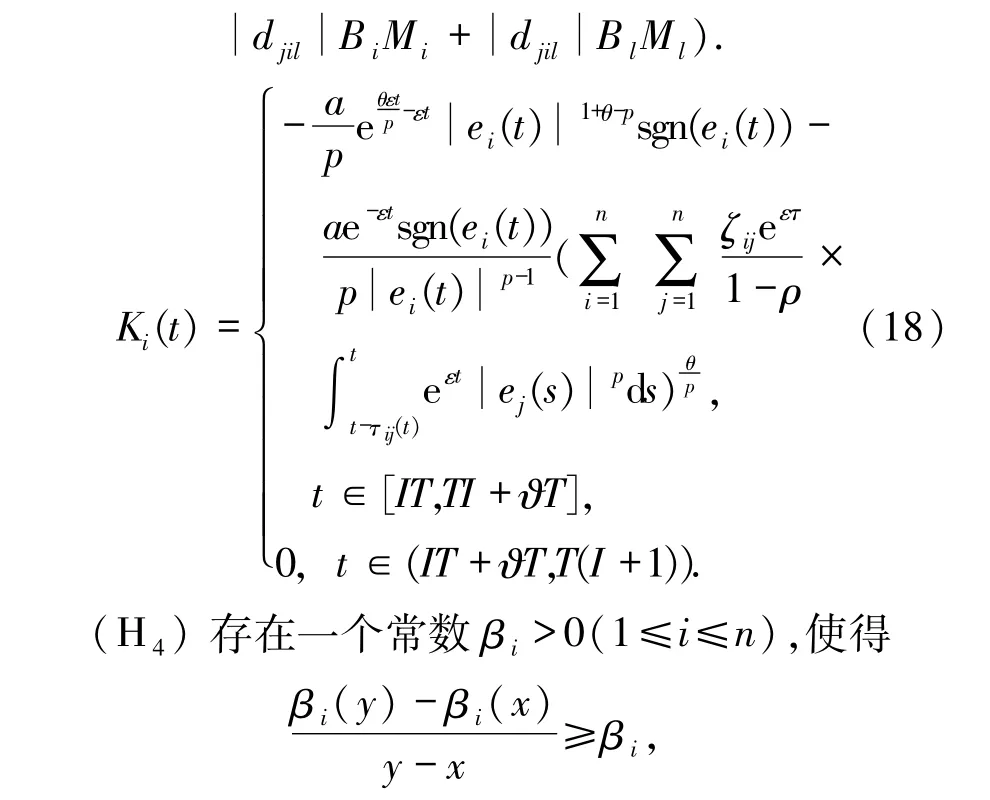
对任意的x，y∈R且x≠y成立.

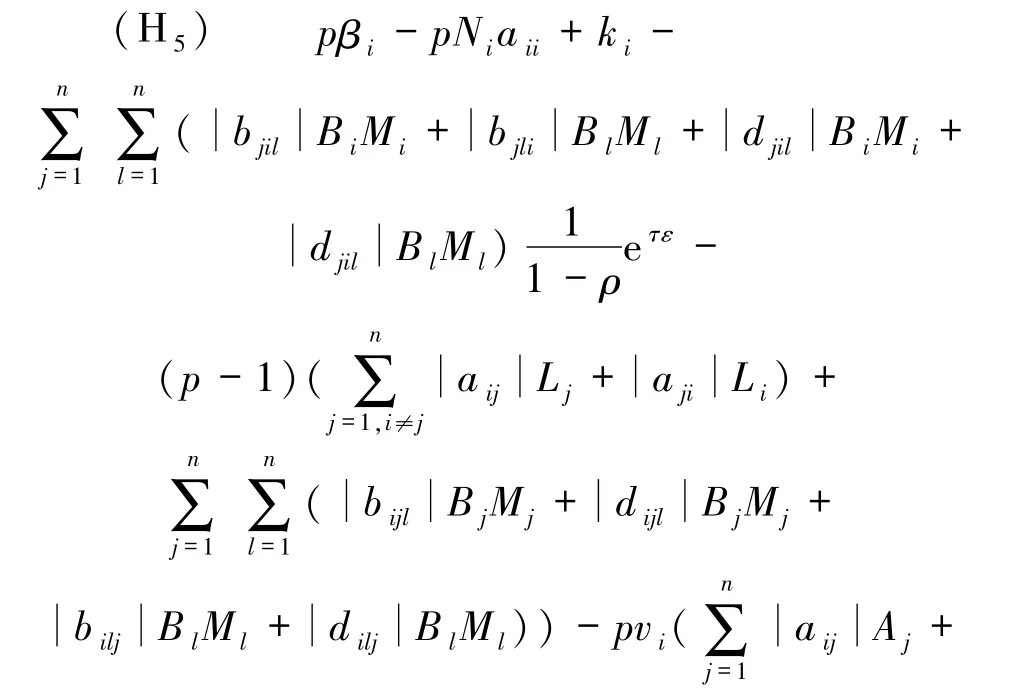
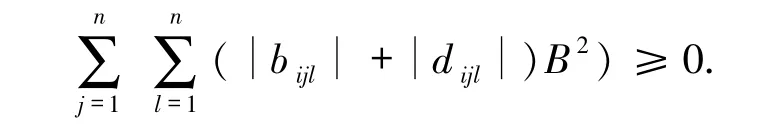
推论 1 若假设（H3）～（H5）成立，在周期间歇外部输入控制（18）式下，则驱动系统（16）和响应系统（17）在有限时间（0，¯T］内是周期间歇同步的，其中（15）式成立

注3 文献［15］通过周期间歇控制的方法研究了一阶时滞递归神经网络的指数同步问题，当时间t→+∞时才能实现神经网络系统的同步；文献［16］通过周期间歇控制的方法研究了一阶具有混合变时滞和反映扩散项的随机Cohen-Grossberg型神经网络的指数同步，由同步定义

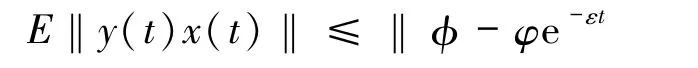
可知，所研究的神经网络系统在无限时间内实现同步.在本文中通过周期间歇控制的方法研究了高阶Cohen-Grossberg型模糊细胞神经网络在有限时间内的同步问题，相对于文献［15-16］本文结论能更加高效的实现所研究的神经网络系统同步.

致谢 遵义市15851人才资助项目（2013、2014和2015年）对本文给予了资助，谨致谢意.