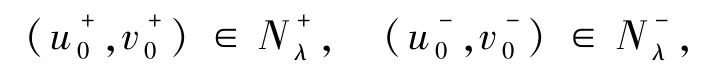带非线性边值条件的奇异P-Laplacian方程组多解的存在性

杜 刚

（喀什大学数学与统计学院，新疆喀什844008）

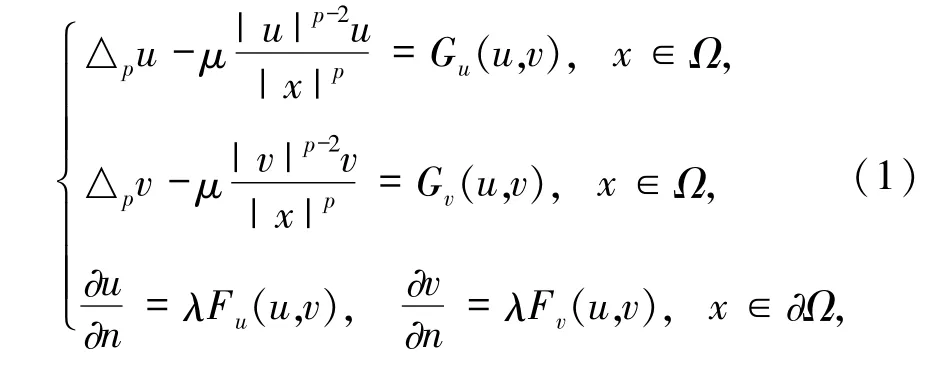
其中，Ω是RN中的有界光滑区域，0∈是单位外法向量＞0，函数F、G满足以下条件：

（f1）F，G∈C1（R2，R+），即对所有的（u，v）∈R2，有

F（u，v）≥0， G（u，v）≥ 0，

且F、G不恒为0；

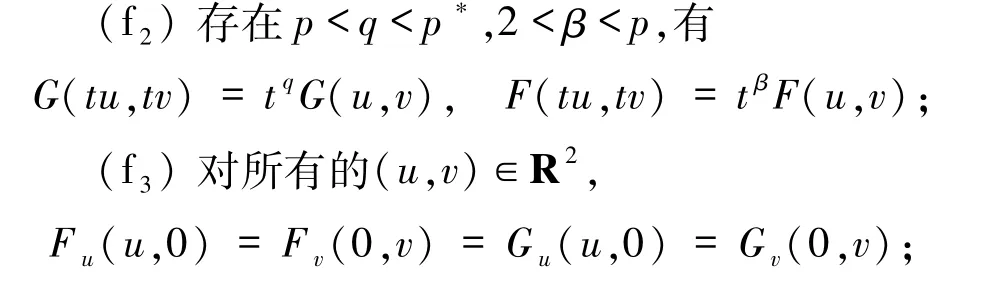
（f4）对所有的（u，v）∈R2，Fu（u，v）、Fv（u，v）、Gu（u，v）、Gv（u，v）关于 u、v是严格单增函数.

近年来，有许多文章研究椭圆方程组在非线性边界下的解［1-5］，文献［1］利用 Nehari流形证明了

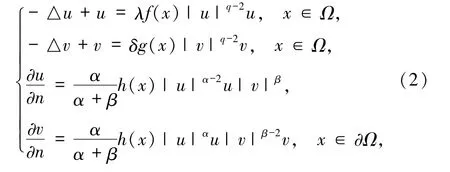
在 f（x）、g（x）满足一定条件下得到了方程正解的存在性.文献［2］用Nehari流形和极值原理得到

我和老伴几十年的感情，前段日子差点败给一次争吵。原本我们感情和睦，但老伴自从退休后变得脾气古怪，只要有人反对她的看法，她不仅听不进去别人的意见，而且还喜欢翻旧账。

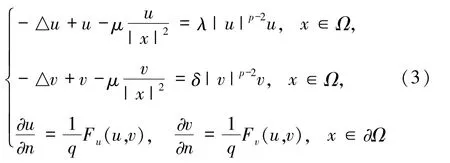
方程组在参数满足一定条件时多个解的存在性.文献［3］也是利用Nehari流形证明了

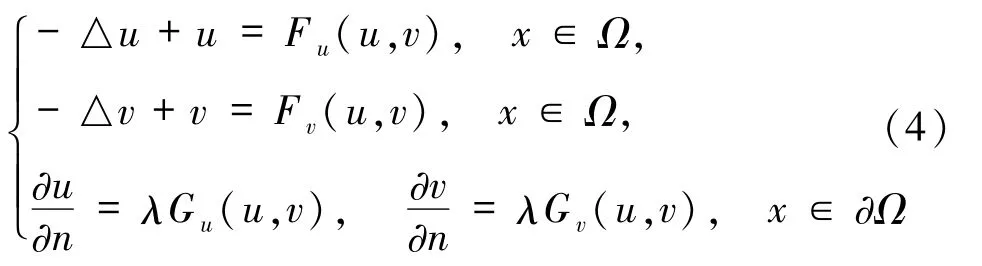
多个正解的存在性.但据了解，对于非线性边值条件的奇异P-Laplacian方程组多解的存在性结果目前还没有.本文将借助Nehari流形和极值原理，得到在λ满足一定条件时，方程组（1）多组正解的存在性结果.本文的主要结果由以下定理给出.

定理 1 若函数 F、G 满足条件（f1）～ （f4），0＜λ，其中

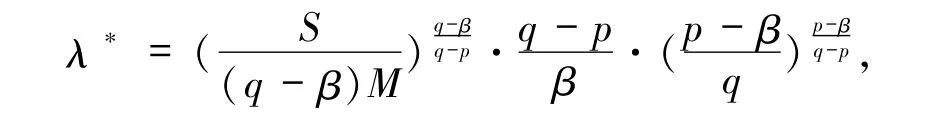
则问题（1）至少有2组正解.

1 预备知识及主要引理

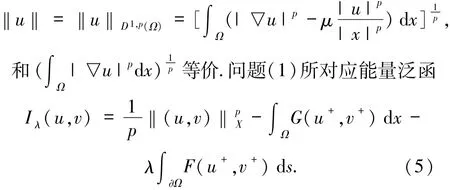
在Nehari流形上考虑这个问题，定义Nehari流形［7-8］Nλ＝｛（u，v）∈X＼（0，0）｜〈I′λ（u，v），（u，v）〉＝0｝，定义

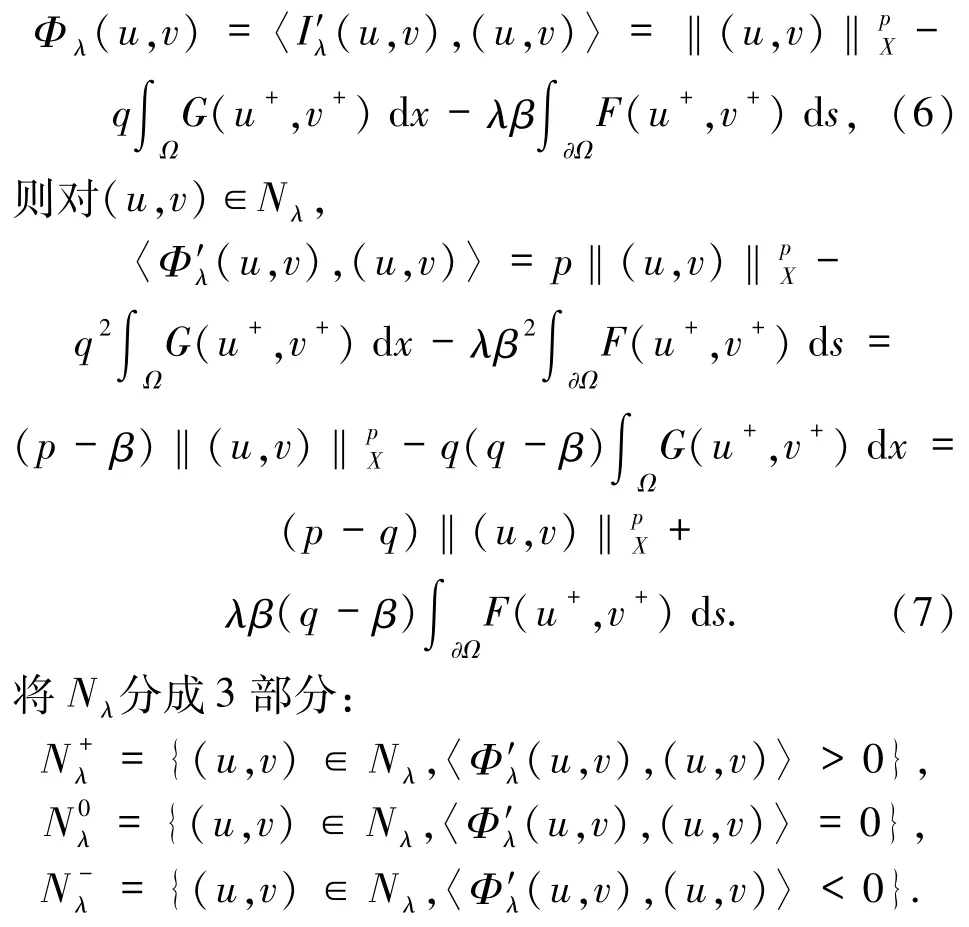
引理 1.1 如果 F、G 满足条件（f1）～ （f4），且0＜λ＜λ*，其中

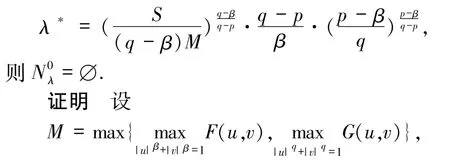
由条件（f1）～（f4）易得

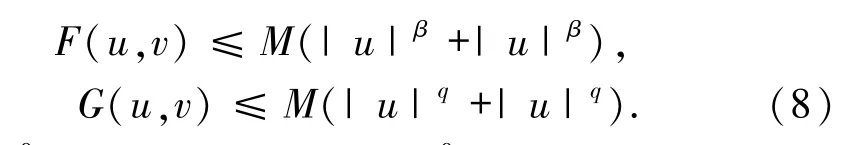
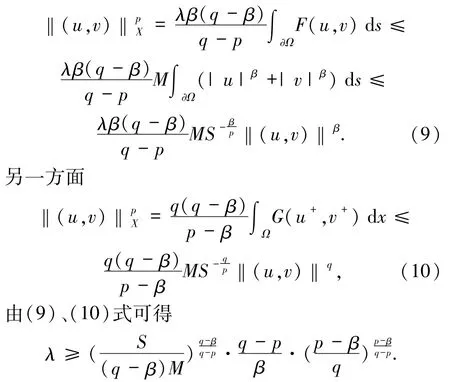
这与条件λ＜λ*矛盾，所以＝Ø.

引理 1.2 假设（u0，v0）是 Iλ在 Nλ的局部极小点，且（u0，v0）∉，则 I′λ（u0，v0）＝0.

证明类似于文献［9］.

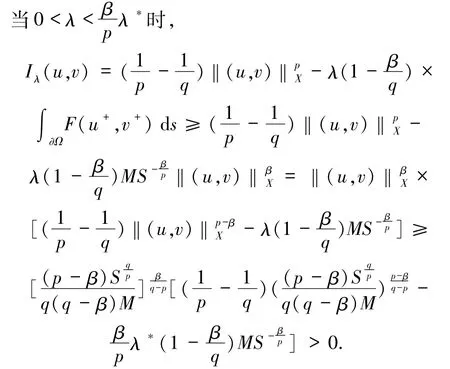
2 主要结论

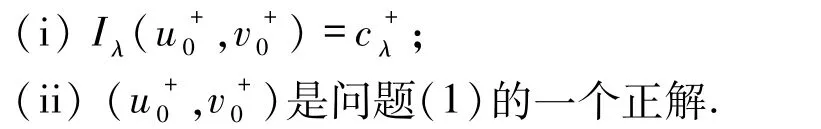
证明 设｛（un，vn）｝是 Iλ在上的极小序列，易证｛（un，vn）｝有界，因而存在｛（un，vn）｝的一子列不妨仍记为｛（un，vn）｝，使得（）∈X是（1）式的一个解且，于（Ω）；，于 Lβ（Ω）；2 ＜ β ＜，，于Lq（Ω），p≤q ＜ p*，这就意味着

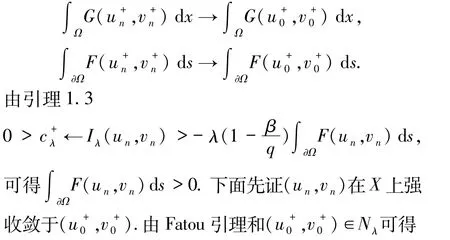
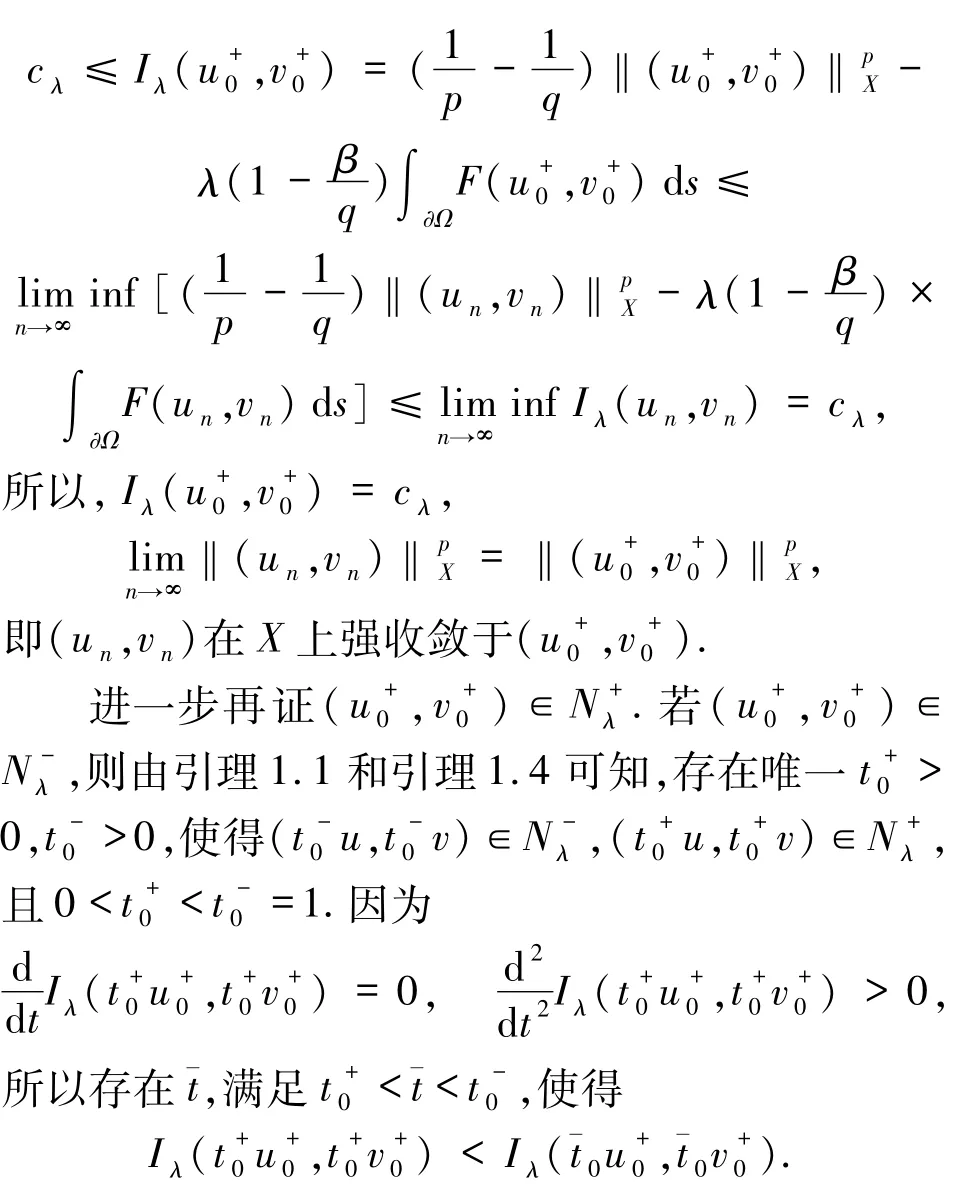
再由引理1.4有

证明类似文献［10］中的定理3.2.

定理1的证明 结合定理2和定理3，存在