基于主动微波遥感的典型黑土区土壤水分反演

张新乐，秦乐乐，郑兴明，谢雅慧，潘 越，邱政超，刘焕军,

（1.东北农业大学资源与环境学院，哈尔滨 150030；2.中国科学院东北地理与农业生态研究所，长春 130012）

土壤水分是建立流域水文模型、监测农作物生长及农业灾害的重要因子[1]。传统土壤水分测量方式费时费力，无法满足大范围空间需求[2]。微波等遥感技术的兴起，为土壤水分监测提供新方法。微波不受光照、云、雾等影响，可穿透土壤、植被[3]。在裸土区，影响微波后向散射系数强度主要因子有土壤水分、粗糙度参数及雷达系统参数等，国内外学者已构建多种模型反演土壤粗糙度和土壤水分[4-5]。

目前利用微波遥感反演土壤含水量模型主要有经验模型（Oh模型、Dubois模型）、半经验模型（Shi模型]）和理论模型（几何光学模型、物理光学模型、小扰动模型、IEM模型和AIEM模型）。在实际应用中，由于理论模型过于复杂，无法直接应用于土壤水分测算，常采用简单经验和半经验模型作土壤水分反演，模型使用雷达系统参数和实地测量数据，精度较高[6]。Shi模型仅适用于L波段，Dubois模型对ks＞2.5粗糙地表散射系数模拟值与实际观测值不符。同前两种模型相比，Oh模型在其适用范围内，可模拟裸露地表后向散射系数，模拟值和地表实测值结果一致。Merzouki等采用C波段Radarsat-2数据评价Oh模型适用性，结果发现选择交叉极化时土壤水分反演效果最好[5]。蒋金豹等采用AIEM模型和Oh模型分别计算同极化后向散射系数和交叉极化后向散射系数，建立后向散射系数与土壤粗糙度关系，利用BP神经网络算法计算裸土区土壤水分含量，反演精度较高[7]。

在雷达系统参数不变情况下，裸土区地表粗糙度和土壤水分是影响雷达后向散射系数主要因素，土壤水分反演需去除土壤粗糙度影响。为减少土壤水分反演中未知数参数，Zribi等提出新粗糙度参数Zs=S2/L，将两个粗糙度函数整合，并在入射角39°和23°下实现土壤水分反演[8]。该方法仅讨论2种入射角，未分析不同入射角和不同极化组合。基于此，本文选取Radarsat-2 VV/VH为影像数据基础，Oh模型为反演基础，黑土区为研究区，与以往经验模型对比，未加入相关长度，仅利用模拟后向散射系数、均方根高度和土壤水分建立函数关系式，消除土壤粗糙度影响，实现裸土区土壤水分反演。考虑不同入射角对雷达后向散射系数影响，该模型无需实地测量土壤粗糙度，可实现大面积土壤水分预测。

1 材料与方法

1.1 研究区概况

选取黑龙江省北安市赵光农场耕地作为研究区，中心位置为北纬 48°2'，东经126°45'，海拔240～330 m。地处中高纬度，属寒温带季风气候，年平均气温一般0.5℃，年降雨量570 mm，年平均日照2 700 h以上。土壤类型主要有棕壤、黑土、草甸土和沼泽土4种，黑土面积占总耕地面积57.4%。野外试验时间始于2017年5月30日，随机选取50个样点。一般当NDVI＞0.4时，植被覆盖对土壤水分影响无法忽略。

研究区如图1所示，以2017年5月28日Landsat8 OLI影像计算NDVI，研究区大部分地区NDVI＜0.4，说明植被对雷达后向散射系数影响较小，可忽略植被影响，研究区当视为裸露地表。下载研究区30 m空间分辨率DEM。由图1可知，该区地势从西北到东南大致呈升高趋势，由西南到东北先升后降。

图1 研究区及地形特征Fig.1 Study fields and terrain features

1.2 试验数据来源

1.2.1 地面数据测量

1.2.1.1 地表土壤水分获取

试验区内以每个样点为中心点，在其周围5 m×5 m区域内，利用环刀测量5个点土壤体积含水量，取平均值作为该点土壤体积含水量。

1.2.1.2 地表粗糙度测量

使用长1.1 m、含109个探针的粗糙度板测量均方根高度和相关长度，两个探针间距0.5 cm，每个采样点沿垄向和垂直于垄向各测1次，取探针顶部坐标分别计算均方根高度和相关长度。采样点土壤水分、均方根高度和相关长度统计结果见表1。

表1 测量结果统计Table 1 Statistics of measurements results

1.2.2 雷达数据获取与处理

获取2017年5月30日Radarsat-2标准波束模式降轨观测全极化数据，入射角高度角平均值为42.624°，最大最小入射角差值为1.35°，可将整幅影像入射高度角视为常数。影像一景面积为25 km×25 km，波长为5.6 cm，频率为5.405 GHz，空间分辨率为8 m×8 m。利用ENVI Sarscape 5.2软件对雷达数据预处理（辐射定标、滤波、地形校正与地理编码），得到所需后向散射系数影像图，提取裸露地表后向散射系数。由于合成孔径雷达成像时，雷达波在反射过程产生斑点噪声。通过雷达影像滤波试验，发现5×5窗口Lee滤波效果较好。经滤波处理后，部分影像滤波前后结果见图2。

图2 部分研究区滤波前后影像Fig.2 Image before and after filtering in some study area

1.3 方法

1.3.1 Oh模型介绍

Oh对不同含水量和粗糙度随机地表作多角度观测，利用后向散射系数，雷达入射角，均方根高度s、土壤体积含水量mv等建立经验模型。模型适用条件为 0.04＜mv＜0.35 cm3·cm-3，0.13＜ks＜6.98，10°≤θ≤70°，如下式所示：

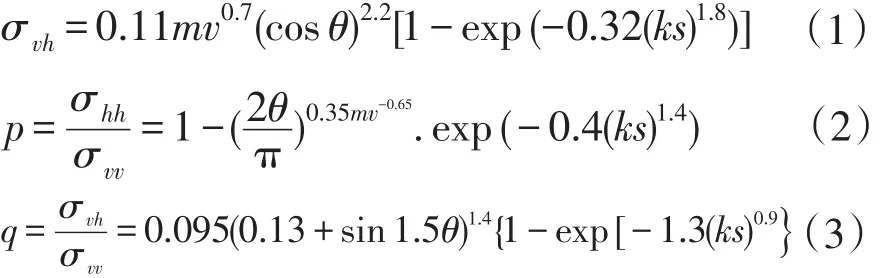
式中，θ为入射角（°）；mv为土壤体积含水量（cm3·cm-3）；s为均方根高度（cm）；k为自由空间波为波长，p为同极化比，q为交叉极化比。

1.3.2 Oh模型适用性分析

选用Oh模型模拟随机地表后向散射系数，首先检验模型适用性。根据改进瑞利准则，将研究区粗糙度划分3个等级：s≤0.33 cm（光滑表面）；0.33 cm＜s＜1.86 cm（中等粗糙面）；s≥1.86（粗糙表面）。

如图3a（不同粗糙度下σvh随土壤水分变化），当s=0.11、0.33、1.86、6.17 cm时，土壤水分区间σvh变化为9.27 dB，而在s区间变化可达21.60 dB。当mv为某一特定值时，s增大，σvh迅速降低，当s≥1.86 cm，σvh不再变化。由图3b（不同粗糙度下同极化比p随土壤水分变化）可知，s越大，同极化比p对mv敏感性越小，当s=1.86 cm时，p在mv湿度区间变化仅有0.90 dB，随s增大，p在区间敏感性逐渐接近0 dB；当mv=0.04 cm3·cm-3时，p在s个区间上动态响应0.54 dB，mv=0.31 cm3·cm-3，p在s区间上动态响应可达3.55 dB，当土壤越干燥或越粗糙时，p变化越小。如图3c（交叉极化比q随粗糙度变化）所示，s越小，交叉极化比q对s敏感性越大，当s≥1.86 cm时，q值逐渐接近饱和，在均方根高度区间q取值＜10.05 dB。

图3 Oh模型适用性分析Fig.3 Applicability analysis of Oh model

通过分析σvh、同极化比和交叉极化与均方根高度、土壤体积含水量关系可知，理论上Oh模型适用范围较宽，但实际上土壤表面非常粗糙或干燥时，则超出Oh模型适用范围。统计研究区地表测量参数发现，土壤体积含水量主要集中在0.1012～0.4424 cm3·cm-3，平均值为 0.2788 cm3·cm-3，相对比较湿润；均方根高度测量值主要在0.3665～1.1065 cm，平均值为0.5779 cm，属于中等粗糙面。Oh模型对研究区土壤湿度和粗糙度敏感，适宜作后向散射系数模拟和水分反演。

1.3.3 经验模型构建

裸露地表后向散射系数主要受地表粗糙度和地表含水量影响[9-10]，关系式为：

式中，m(Zs,θ)是与粗糙度相关函数，n（mv,θ）为与土壤含水量相关函数。

在给定范围内，后向散射系数与土壤粗糙度和水分呈良好对数关系。在一定入射角下，后向散射系数与地表粗糙度和土壤水分关系式为：

σvv=A*ln(Zs)+B*ln(mv)+C*ln(Zs)*ln(mv)+D（5）

通过最小二乘法即可求得经验系数A、B、C、D。

考虑不同极化下后向散射系数与地表粗糙度和土壤含水量关系，发现σvh与土壤含水量和粗糙度存在良好对数关系。在该极化下可得到类似表达式：

本文研究区域较小，入射角变化较小，所以假定入射角不变，将测量所得土壤粗糙度和水分及模拟后向散射系数带入上述经验模型，联立（5）、（6）两式建立方程组消去粗糙度参数，即可求得土壤水分含量mv。粗糙度通常用均方根高度、相关长度或者两者组合Zs衡量。研究区土壤为中等粗糙度，故选用自相关函数（Zs=s/l）。建立后向散射系数与土壤水分与粗糙度关系，使用Zs建立定量关系式如下。联立两个方程组消去粗糙度参数，得到土壤水分反演模型，利用验证点验证，相关系数R2=0.568，模拟精度相对偏低。利用均方根高度替代组合粗糙度建立经验模型。

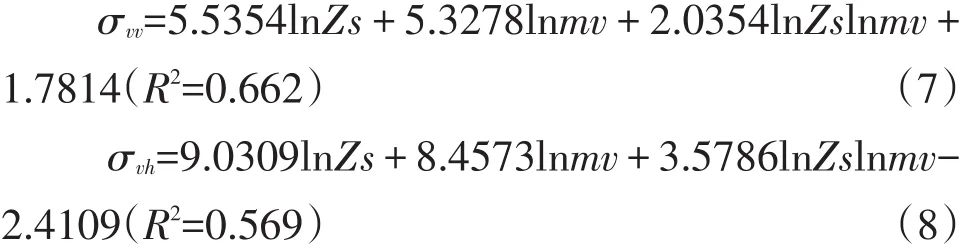
2 结果与分析

2.1 不同入射角条件下模型适用性分析

本文研究入射角42°后向散射系数与mv及s之间函数关系。为确定不同入射角下模型适用范围，对Oh模型设置输入参数为θ=（10°,20°,30°,40°,50°,60°），s∈(0.1,2.1),mv∈（0.05,0.45）。其中，s步长为0.1，mv步长为0.02，建立不同入射角模拟数据库。通过最小二乘拟合得到不同角度反演模型对应A、B、C、D值。表2为不同雷达入射角下经验系数结果。

2.2 模型应用与验证

对试验区采样点作后向散射系数模拟，如图4所示。

由图4可知，其中VH极化模拟效果最好，相关性为0.809，均方根误差为1.24 dB；HH极化相关系数为0.725，均方根误差为1.65 dB；VV极化相关系数为0.694，均方根误差为2.11 dB。从3种极化整体趋势看，模拟值和影像值具有相关性，应用模拟值反演分析水分具有参考价值。

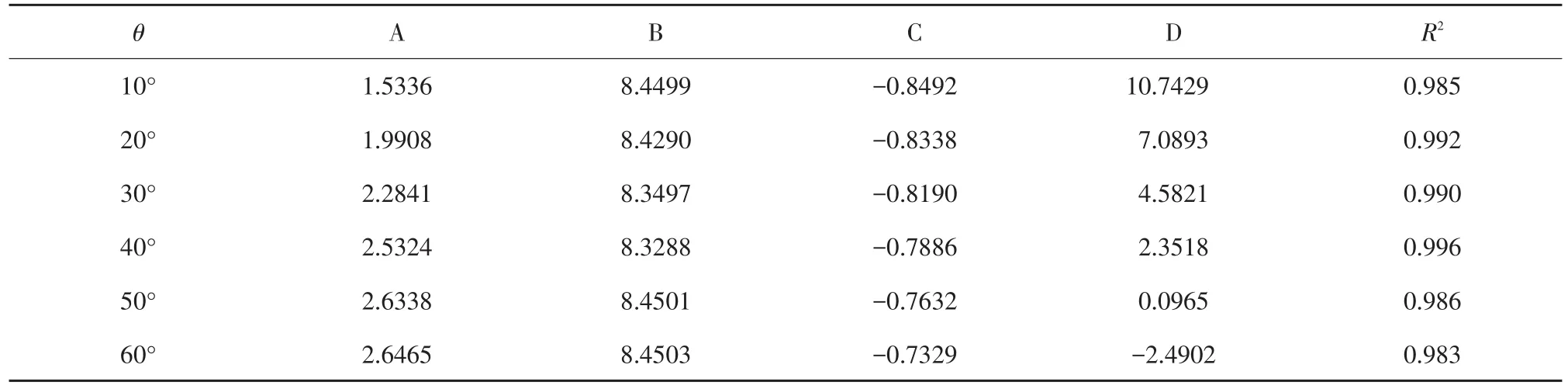
表2 不同入射角下模型经验系数Table 2 Empirical coefficients of the model under different incidence angles

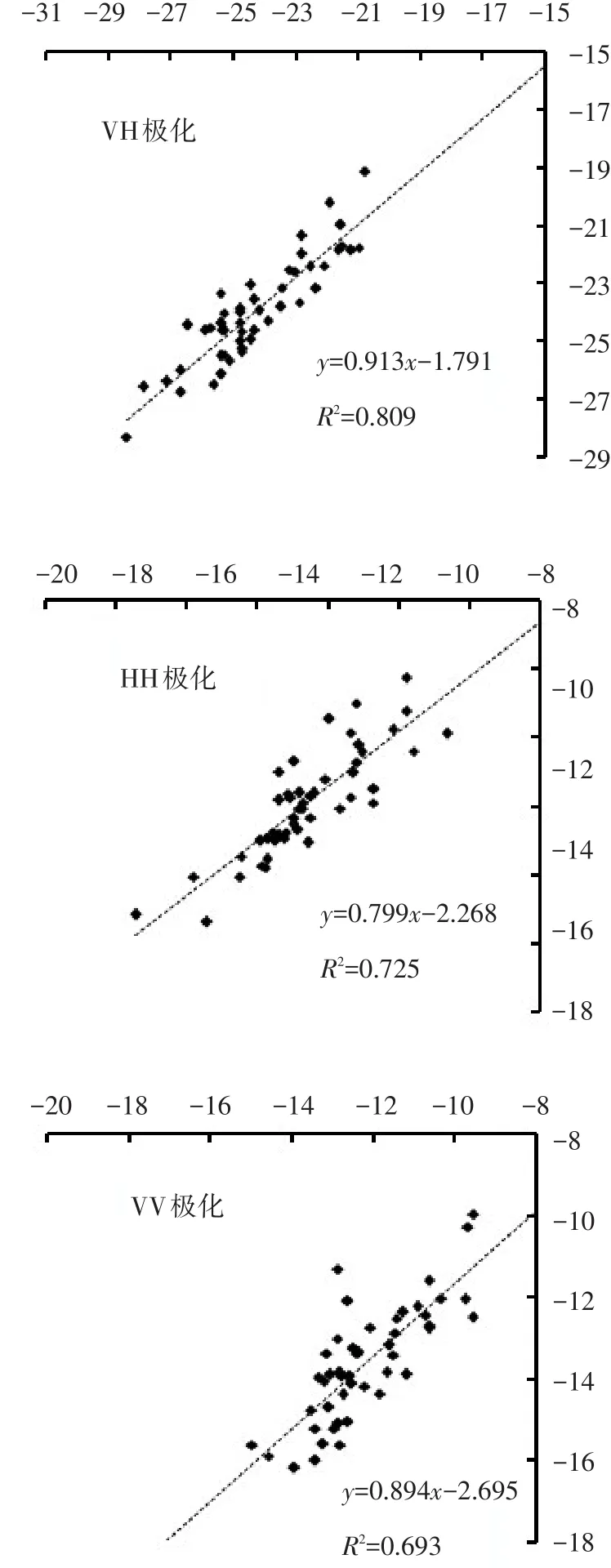
图4 采样点模拟值与RADARSAT-2实际值对比Fig.4 Comparison of simulated values of sampling points with actual value of RADARSAT-2

影像入射角变化较小，采样点在影像上分布较集中，不再考虑入射角变化。本文用41个点构建经验模型，其余点作精度验证。将建模点均方根高度、土壤水分以及推算后向散射系数分别带入式（9）和式（10），通过最小二乘法求解两个方程式经验系数，可得如下两式：

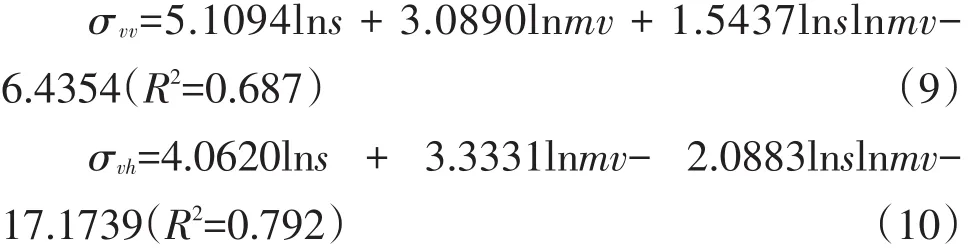
为验证模型模拟效果，根据研究区实测数据分析模型计算结果。剩余9个样点作为验证点，精度验证模型。

基于经验模型反演验证，利用反演土壤水分含量与实测数据对比结果见图5。模型反演值与实际测量值相比总体偏小，且具有明显相关性，RMSE为7.20%，平均绝对误差为0.0530 cm3·cm-3。表明该经验模型模拟值与实际观测值有较好相关性和较小误差，可利用该模型作裸土区土壤水分监测。

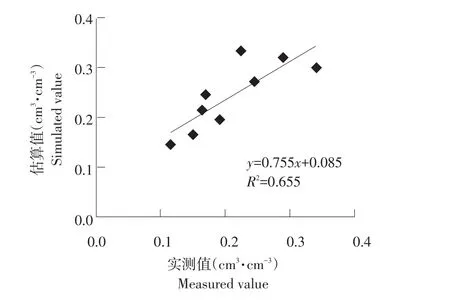
图5 模型反演数据与实测数据关系Fig.5 Simulated soil moisture vs ground measurements

将反演模型应用于研究区，对结果分类，得到研究区土壤水分分布，如图6所示。整体分布上土壤水分值绝大多数＜0.36 cm3·cm-3，反演模型计算结果与该区域内土壤水分分布状况基本相符。地形对土壤水分空间分布有重要影响，由水分分布图可知，研究区东南部水分明显高于西北地区；从东西向看，研究区以北地区，水分由西向东逐渐升高，以南地区水分由高到低再升高；从南北方向看，水分从南往北呈递增趋势。土壤水分空间分布情况符合地势走向规律，可证明模型适用性。图像橘红色亮斑状区域为SAR斑噪，难以完全消除。图像西南部和偏西部植被比较密集（此时植被尚未萌发），植被散射雷达观测数据较无植被覆盖裸土区偏大，水分预测值偏大。另外。从图像中可知部分地块反演值大于0.35 cm3·cm-3，实地调查证明，其中存在洼地或坑塘。Oh模型无法反演湿度过大土壤，洼地和坑塘占地面积很小，此部分区域精度不再检验。

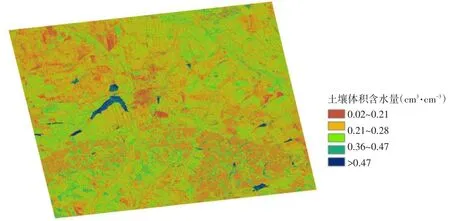
图6 研究区土壤水分反演Fig.6 Soil moisture distribution map in the study area

3 讨论

遥感技术在农业上应用广泛，大多利用光学遥感、微波遥感对裸地、植被覆盖等地表作土壤水分监测。利用主动微波遥感对小尺度地块作水分监测研究较少。本文利用高分辨率雷达数据预测区域尺度黑土农田水分，验证主动微波遥感在小尺度地块适用性。

东北黑土区地形起伏变化相对较大，土壤侵蚀程度不同，地形土壤水分空间分布差异较大。垄型结构耕地旱涝灾害监测和作物长势监测具有重要应用价值。研究以全极化8 m分辨率Radarsat-2数据、30米分辨率DEM数据、地面实测数据为数据源，系统分析影响雷达后向散射系数因子，建立反演模型预测试验区内土壤水分分布状况。首先利用Oh模型模拟各极化模式下雷达后向散射系数，发现VH极化下理论模拟值与雷达实测值相关系数最高，与尹楠[11]研究结果一致。建立后向散射系数与土壤水分、土壤粗糙度之间函数关系式，采用最小二乘法计算土壤水分含量，与张祥等[12]研究结果一致。本文预测精度相对偏低，原因是变化检测模型更宜去除表面粗糙度，今后研究可引入不同时相数据估算水分变化。BP神经网络模型作水分预测需大量样本输入，输入参数须根据实际地表情况，重新采样，耗时耗力，本文基于交叉极化数据建立经验模型，消去粗糙度参数，地表状况在模型适用范围内，直接预测土壤水分，避免多次采样建模。实际野外采样中，地表相关长度难以精确测量，交叉极化后向散射系数对垄向数据不敏感，水分预测结果精度不高（R2=0.585），本文建立仅包括均方根高度和土壤水分两个未知数参数经验模型，解决野外测量相关长度不精确等问题，减少方程式中未知数参数，易于土壤水分计算，精度明显提高。本文研究方法理论基础为电磁波辐射传输方程地表散射模型，结合研究区土壤质地等参数，相比其他模型（研究区之前利用光学遥感影像提取反射率建立模型，研究结果R2=0.487）具有适用广泛、精度高等优点。当土壤表面处于中等粗糙度时，模型可预测土壤水分。利用C波段雷达影像数据预测分析区域尺度农田水分，证明主动微波遥感可反演裸土区土壤水分含量，反演精度较高。

本文建立模型对研究区土壤表层水分预测适用性强，对地表微起伏其他农田地块反演效果较好，但深层土壤和植被覆盖地表土壤水分反演存在误差。今后将加强对地观测试验。①试验结果可知，Oh模型对干燥和粗糙度较大土壤敏感性较差，均方根高度难以精准描述复杂自然地表地区，最终反演结果误差较大，可进一步精准测量试验区土壤粗糙度、土壤质地等参数，建立适合黑土区微波遥感反演土壤水分经验模型，或利用其他极化组合方式反演。②本文主要研究地表层，但土壤深层及有农作物覆盖地表含水量不同，且雷达入射波对不同地表穿透力不同，消除叶片、冠层等对雷达后向散射系数影响，建立适合所有地表土壤水分预测模型，有待于深入研究。③研究区采样点较集中，影像入射角变化小，研究过程中将整幅影像平均入射角作为输入量，视为常数，未考虑入射角变化对土壤水分反演结果影响，模型应用于大尺度区域时需考虑入射角影响。另外，模型中入射角处理依赖于Oh模型推导和验证，利用模拟数据建模时，简单线性拟合将入射角加入模型中降低模型精度，需探讨新入射角处理方法。

4 结论

基于研究区实际情况，以Oh模型为模型反演基础，模拟裸露地表后向散射系数，分析影响裸土区土壤水分反演因素，利用交叉极化数据建立适合黑土区土壤水分反演经验模型，最终得到研究区土壤水分反演图。通过对比验证，结论如下：

a.通过各模型分析比较，确定Oh模型反演裸土区土壤表面水分含量。研究基于野外实测数据和Radarsat-2全极化数据，发现模型模拟出后向散射系数与雷达影像转换得到后向散射系数相关性较好，在VV、VH极化模式下，拟合相关数分别为0.693、0.809，在此基础上，可进一步讨论HH、HV极化、同极化差与粗糙度关系，得到全极化下土壤水分反演模型，提高水分反演精度。

b.针对裸土区土壤水分监测，分析后向散射系数与土壤水分、均方根高度之间关系，利用最小二乘方法拟合经验系数，提出新经验模型。该模型仅有两个未知数参数（s和mv），运用Radarsat-2VV、VH交叉极化数据即可作地表土壤水分测算。

c.研究提出两种裸露地表土壤水分预测模型，一种建立组合粗糙度与土壤水分关系式，一种建立均方根高度与土壤水分关系模型。对比发现：使用组合粗糙度代替均方根高度建模，模拟精度降低15.32%，验证本文模型有效性。

d.利用实测数据验证经验模型，反演精度较高，预测结果与实测数据拟合关系较好，平均绝对误差为5.30%，其中7个检验点相对误差在10%以内，2个点相对误差大于10%，证明本文提出经验模型与Oh模型联合反演裸露地表土壤水分反演方法可行。