多智能体领航跟随一致性和轨迹跟踪问题研究

林 敏，夏元清，吴 爽

（北京理工大学自动化学院，北京 100081）

1 引 言

随着移动机器人技术的发展以及通讯技术、计算机小型化技术的日益成熟，将一个复杂的任务分配给多个结构、功能都相对简单的智能体来完成已经成为了一个热门的研究方向。多智能体协同完成一项任务在军事、民用等领域都有很大的发展潜力。目前的典型应用有集合［1，2］、编队控制［3，4］、集群［5，6］以及任务分配［7］等。

多智能体系统一般都具有智能体数量大、分布式感知、复杂通讯的特点，智能体之间经常存在着彼此的信息交互，因此用图论来描述这种信息交互渠道就显得十分自然。在一个多智能体系统中，若一个智能体能将自身信息传给另一个智能体，那么就可以将这种通讯关系描述成两个结点间以一条有向边连接。若这两个智能体间能互相将自身信息传给对方，这种通讯关系则可以描述成两个结点间以一条无向边连接。若两个智能体间的通讯联系关系随着它们间距的增大而减弱，则可描述为两结点间边的权值减小。由此，多智能体通讯拓扑网络就能完全用图来描述，进而用图论中的代数方式来描述和研究通讯拓扑的性质和编队的性质。

代数图论借助矩阵代数的方式来描述图及其变换与性质。多智能体控制算法中经常用到邻接矩阵来描述编队的通讯拓扑，用拉普拉斯矩阵证明编队的稳定性［8］、收敛速率等关键性质。

在基于图论的方法中，刚性图理论也得到了关注。“刚性”就是指当无向图顶点运动后，每个顶点间距得以保持的性质。刚性图理论最早诞生于机械领域，后被应用于多智能体编队控制。基于刚性图论，可以方便地通过算子描述刚性编队的分裂和重组［9，10］，还可以利用智能体间距设计编队控制律以确保刚性。基于同样的理论，Anderson团队研究了多智能体编队的刚性保持和队形切换，解决了队形变形、分裂、合并问题［11］，做出了许多原创性理论贡献。

本文在基于图论的一致性编队算法基础上，加入人工势能场避障方法，使得跟随者收敛至领航者坐标系下的理想位置时可以避开环境障碍物，且跟随车辆之间不会相撞。同时，针对具有非完整性约束的轮式机器人模型设计了领航者轨迹跟踪算法，使得领航车辆以期望的速度角和速度行驶在规定的轨迹上。最终实现“行星-卫星”式编队，即领航者为有固定轨迹的“行星”，跟随者为“卫星”，始终以一定的半径围绕领航者行驶。最后通过仿真验证了算法的有效性。

2 背景知识

2.1 图 论

用有向图或无向图来对多智能体间的通讯拓扑进行建模，可以将通讯拓扑结构代数化，从而能借用矩阵的性质对通讯图的连通性等关键性质进行研究。在这部分介绍一些图论中的符号以供后续使用。

一个由n个智能体组成的多智能体系统，可以用图中的n个顶点代表这n个智能体，用图的边代表这些智能体间的通讯拓扑连接关系。由于智能体间的通讯都是有向的，所以一般用有向图来描述多智能体系统的通讯拓扑。当系统中有通讯关系的两个智能体间的通讯都是双向的时，可以将有向图简化成无向图。

一个有向图G由一个有限顶点集合以及一个边集ε⊆V×V组成，其中边是一对顶点的有序对。定义有向图的邻接矩阵为其中的元素都是非负的，表示V的基。如果(i,j)是G的一条边，即(i,j)∈ε，意味着从i到j有一条有向路径，那么元素aji是正数，否则为0。规定对任何都有(i,i)不属于ε。记智能体i能通讯到的所有智能体的集合为称作智能体i的通讯集。如果一幅有向图中存在一个称作根的顶点，使得它到其他所有顶点都有路径连接，则称这幅有向图存在有向生成树，该顶点称作生成树的根。顶点i的度di定义为用D表示di的N×N的对角阵，那么D就是图G的度矩阵。图G的拉普拉斯矩阵就用半正定矩阵L=D-A来定义，或也可以定义为其中：

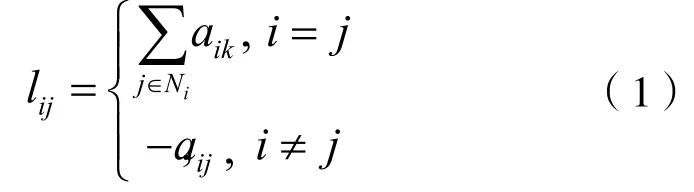
拉普拉斯矩阵是图论中十分重要的一个矩阵。从式（1）中可以看出拉普拉斯阵L的行和为0，因此一定有一个零特征根，且L的特征根总是非负实部的。L中有几个零特征根，则代表图中有几个连通子图（即独立的子网）。若用表示拉普拉斯矩阵L的m个特征根，且

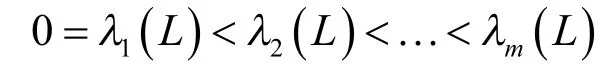
2.2 系统模型

考虑一个含有n个智能体的系统，为全局坐标系下的位置，为速度方向与坐标系x轴的夹角，为线速度，为角速度，则根据运动学模型容易获得领航者模型为：

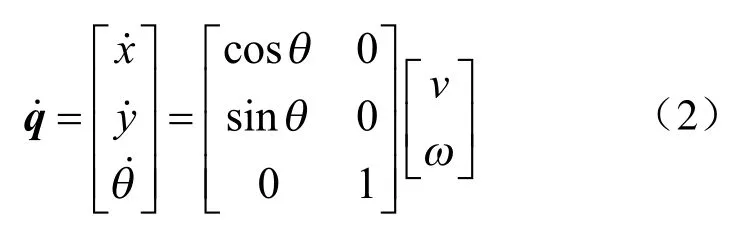
对于跟随者，为了简化一致性控制算法，采用简单的一阶积分器模型如下：

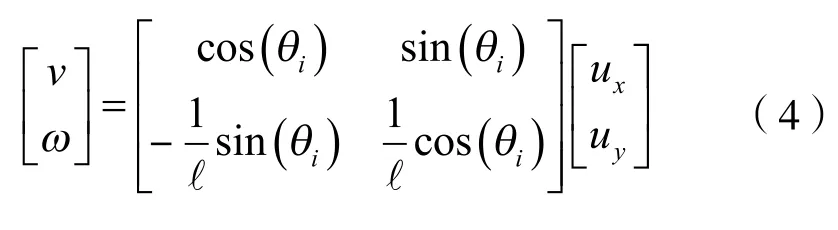
3 领航者轨迹跟踪算法

在实际应用中，领航者的轨迹通常是很复杂的，为了让领航者能以预期的角速度和线速度走在某个特定预期轨迹上，同时也为了让其预期轨迹更加多样，就需要对领航者施加轨迹跟踪算法。即设计控制律使小车实现对参考位姿参考线速度vr和参考角速度ωr的跟踪。轨迹跟踪模型如图1所示。

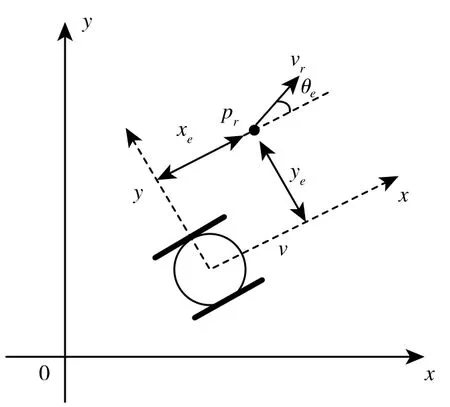
图1 轨迹跟踪模型示意图

由图1中的几何关系，首先写出小车当前位姿与参考位姿之间的误差模型：

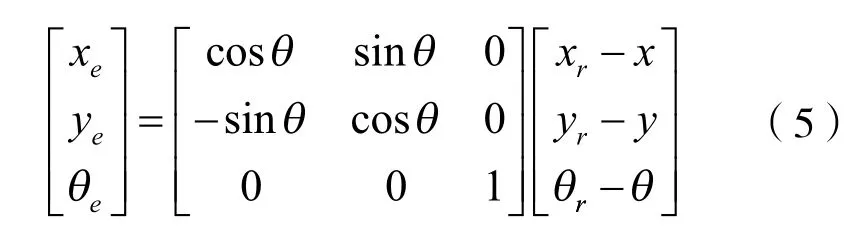
对式（5）左右两边求导，结合小车运动学模型式（2），可得：

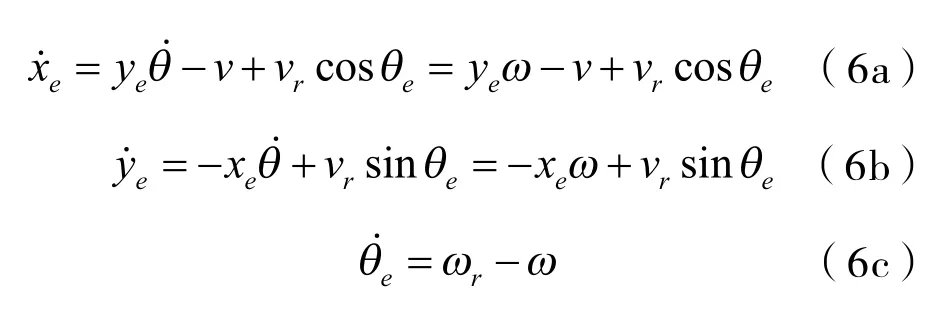
注1.从式（6）中可以看出，当参考角速度ωr为0的时候，ye的收敛依赖于θe。若在ωr=0的前提下，θe将早于ye收敛到0，那么ye将变得无法控制，这就是在设计轨迹跟踪算法时要注意的控制奇异点的问题。为了解决这个问题，可以在设计控制律时采用引导角［13］，即在ye未收敛时先控制θe为某一非零角度，这样就避免了控制奇异点的产生。本文中引导角设计为：

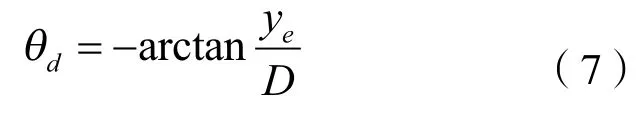
其中D＞0是引导角参数，

定理1.对于具有非完整性约束的轮式机器人，可设计如下控制器（8）和（9）保证系统稳定。

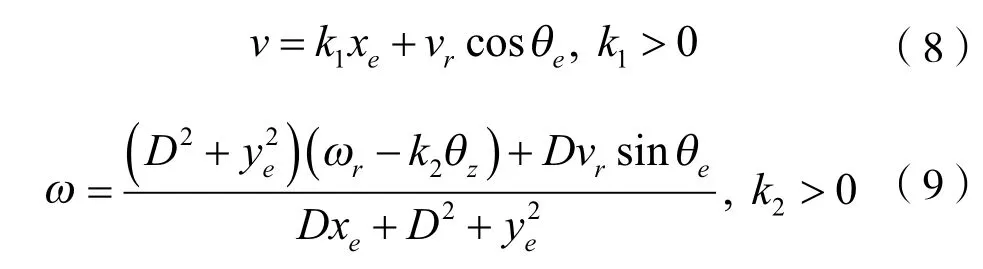
证.首先针对xe,ye的收敛，设计如下Lyapunov函数：

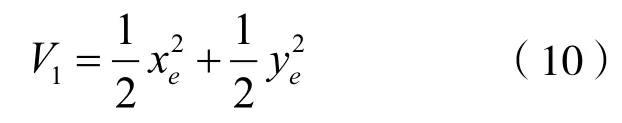
对式（10）求导，代入式（6）可得

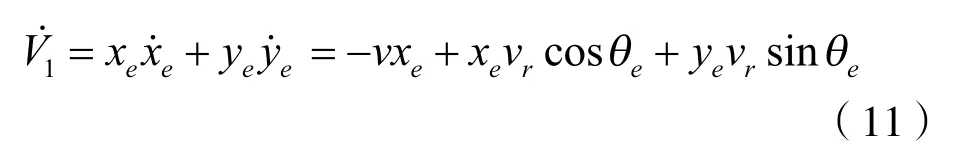
将控制器（8）带入式（11）可得

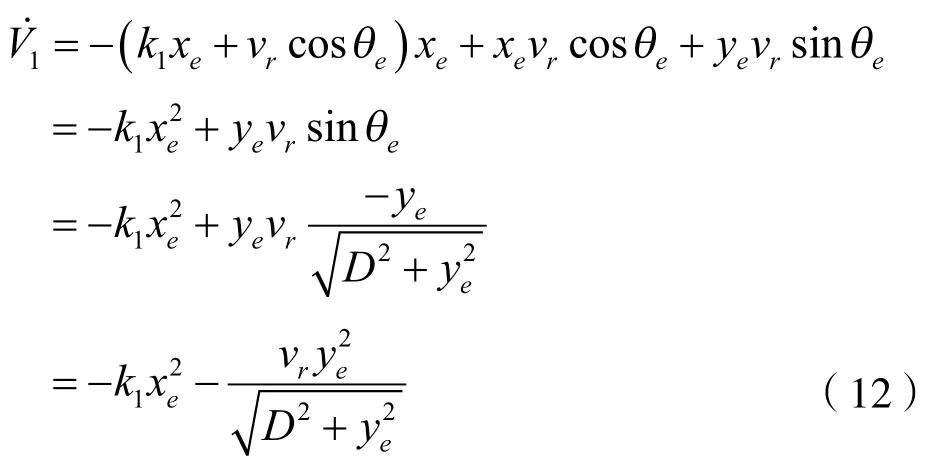
由于k1,vr＞0，所以则当θe为一特定角度时，ye可以收敛。

接下来针对θe的收敛，设计Lyapunov函数：

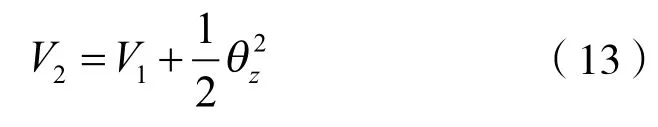
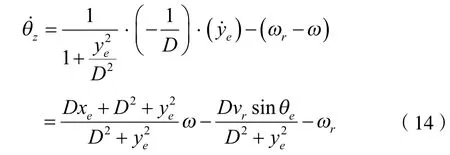
对式（13）求导得

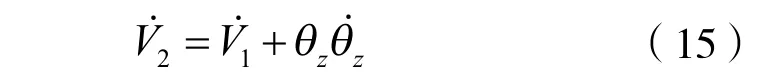
将控制器（9）和式（14）带入式（15）可得

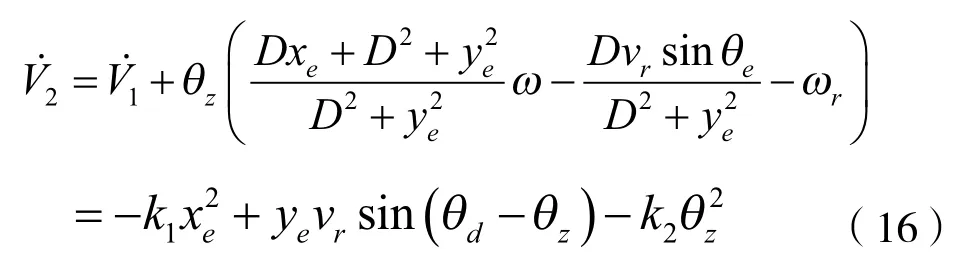
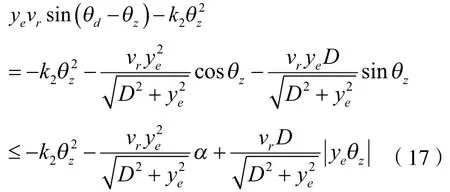
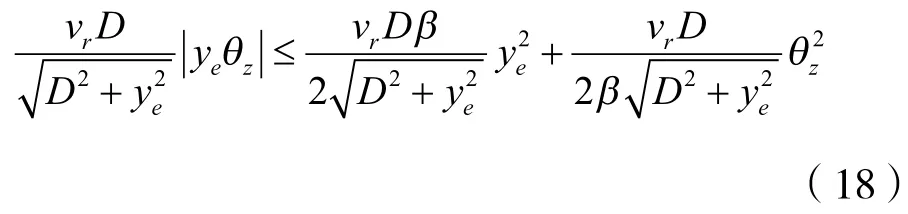
将式（18）带入式（17）可得：

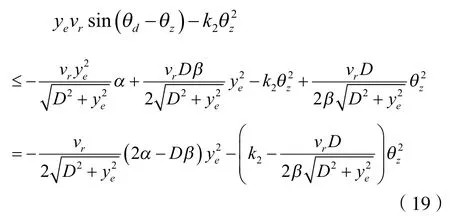
结合式（16）与式（19）可得：

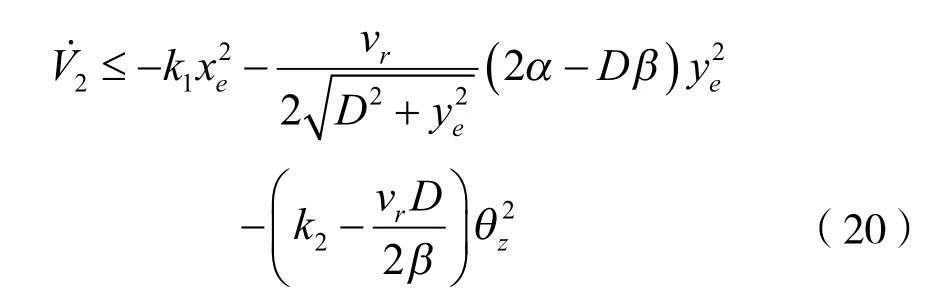
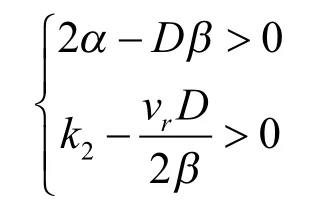
由此解得：

4 跟随者一致性算法

引理1.一阶积分器模型在有向固定/切换拓扑下的连续时间基本一致性算法如下［14］：

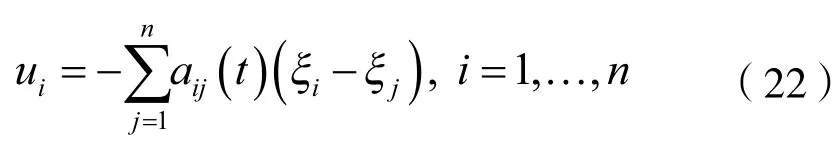
式（22）达成一致性的条件为无向图连通或者有向图存在生成树，在拓扑结构切换的情况下，达到一致性的条件为拓扑结构图的并集对应的无向图连通或者有向图存在生成树。具体的证明可见文献［15］。

定理2.当系统存在领航者，且领航者位置时变时，为使跟随者与领航者的位置量保持一个可时变的偏差，可设计如下控制器：

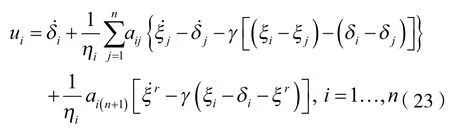
证.令式（23）可化简为：

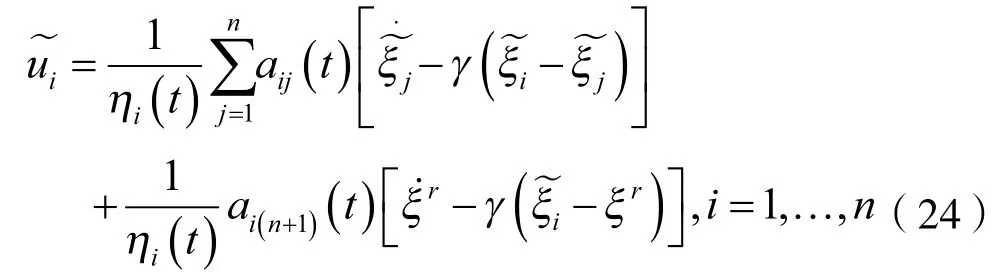
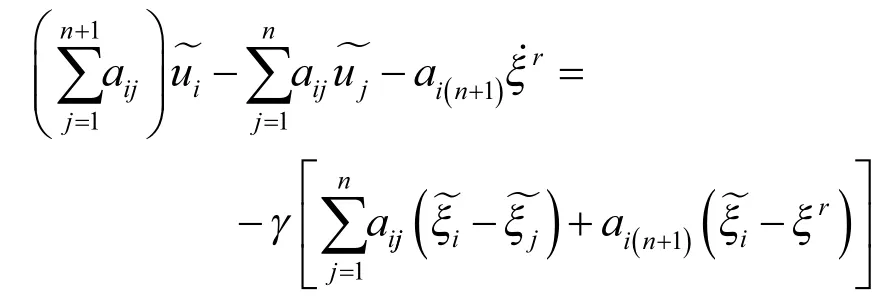
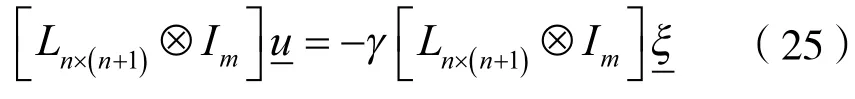
注意到，因为第n+1个智能体是领航者，不需要接收其他节点的信息，所以对应邻接矩阵An+1的最后一行全为0。又因为有向图Gn+1存在有向生成树，所以An+1没有其他全为0的行。于是对应的拉普拉斯矩阵Ln×(n+1)的秩为n。将Ln×(n+1)写成由于Ln×(n+1)有行和为0的性质，所以其第n+1列取决于前n列，即：

所以，有向图Gn+1存在有向生成树的充要条件是

于是式（25）可以写成：

由于矩阵M满秩，所以可逆，因此有：

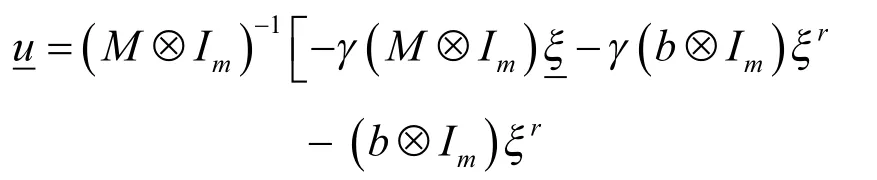
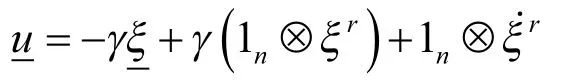
即：

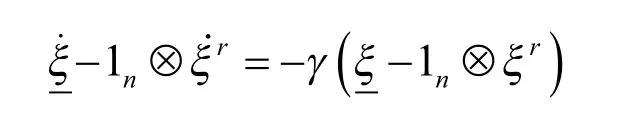
由上式可看出当t→∞时，也就是当且仅当有向图Gn+1存在有向生成树。

5 基于人工势能场的避障算法

对于避障控制，最广为采用的方法就是由Khatib于1986年提出的人工势能场方法［16］。机器人在人工势能场中的运动可以类比于带电粒子在电场中的运动。在电场中，带电粒子沿着电场的梯度向量方向运动，由高势能点向低势能点运动，梯度可以看作是作用于带电粒子上的力。在机器人的运动过程中，可以将机器人看作在势能场中运动的粒子，障碍物对这个粒子产生排斥力，运动的目标点对这个粒子产生吸引力，在引力和斥力的作用下，粒子就能在向目标点前进的过程中避开障碍物。

在本文讨论的情况中，由于每个智能体都有自己需要跟踪的轨迹，不需要额外设置产生吸引力的势能函数，只需设置产生斥力的势能场进行避障即可。对于运动的车辆来说，产生斥力的势能场来自于与之邻近的其他车辆。只有其他车辆进入到其避障范围内时，势能场就迅速升高，产生排斥力，而在避障范围外，势能场就为0。图2是这种势能场的示意图。

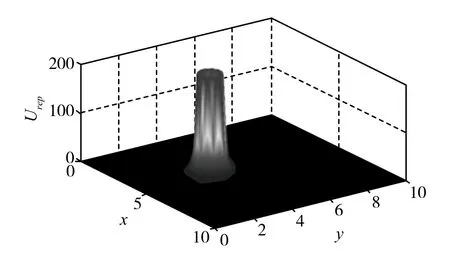
图2 人工势能场示意图

设计势能函数如下：

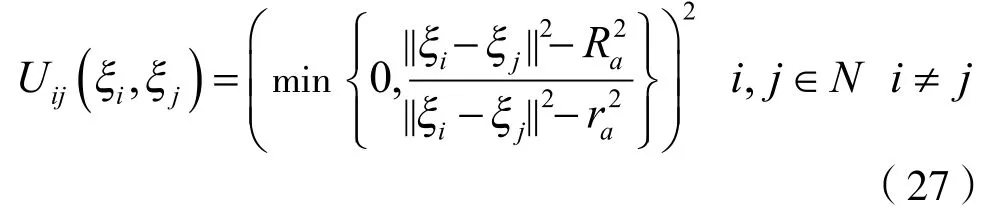
其中，Ra＞ra＞0，||·||表示向量的范数，若无特殊说明，默认是2-范数。此势能函数取值如下：

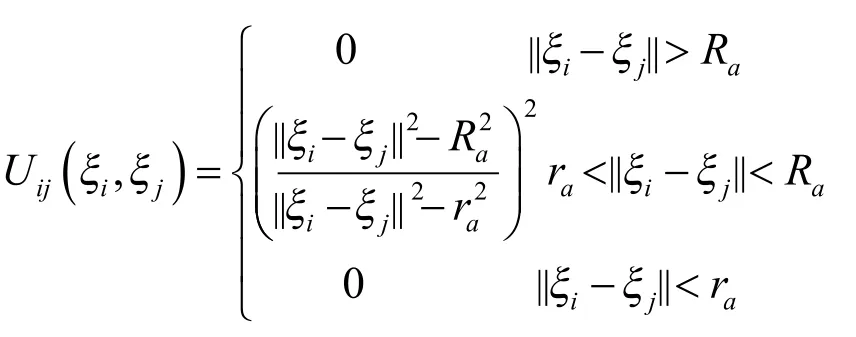
那么小车受到的力就是沿着势函数的负梯度方向，作为小车的避障输入：

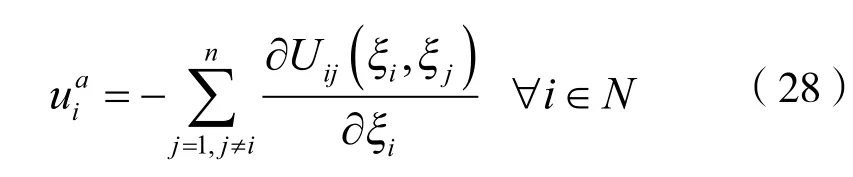
则跟随车辆的控制器可在式（23）的基础上重新设计为：

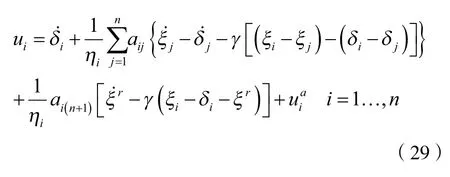
6 仿真结果及分析

本节选取了一辆领航车和两辆跟随车对上文中提到的算法分别进行数值仿真，三辆车之间的网络拓扑关系由邻接矩阵表示为：

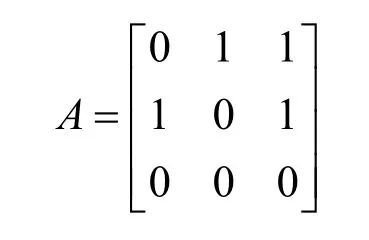
对于领航者的轨迹跟踪算法（8）和（9），在具体仿真时，选择k1=k2=1，L=0.5，使领航者以vr=1，ωr=0.6行走在一个圆形轨迹上。得到仿真结果如下：图3为领航者期望轨迹与实际轨迹，图4为x,y与θ方向上的跟踪误差，图5、图6分别为期望速度、角速度与实际速度和角速度的比较情况。由仿真结果可得，算法（8）、（9）可保证领航者以期望的速度角速度行驶在规定轨迹上。

对于带有人工势能场避障的跟随者一致性算法（29），令γ=2，Ra=0.5，ra=0.25，先任意给定领航者速度vr=0.5，ωr=0.3，当期望误差δi=δj=0时，可得到图7轨迹，表明算法（29）可使跟随者位置达到一致，为了便于观察给出图8为x方向上位置收敛情况。

将领航者轨迹跟踪算法（8）和（9）与跟随者一致性和避障算法（29）结合，同时令即跟随者以领航者为圆心画圆。其中最终可实现“行星-卫星”式编队，仿真效果如图9。

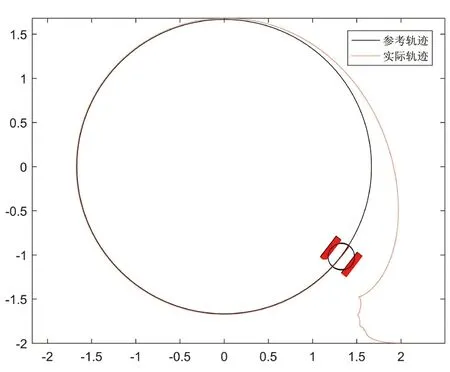
图3 领航者期望轨迹与实际轨迹

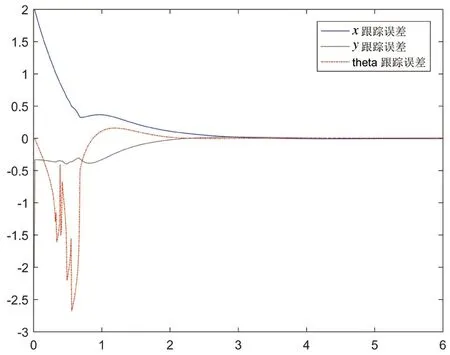
图4 领航者追踪误差

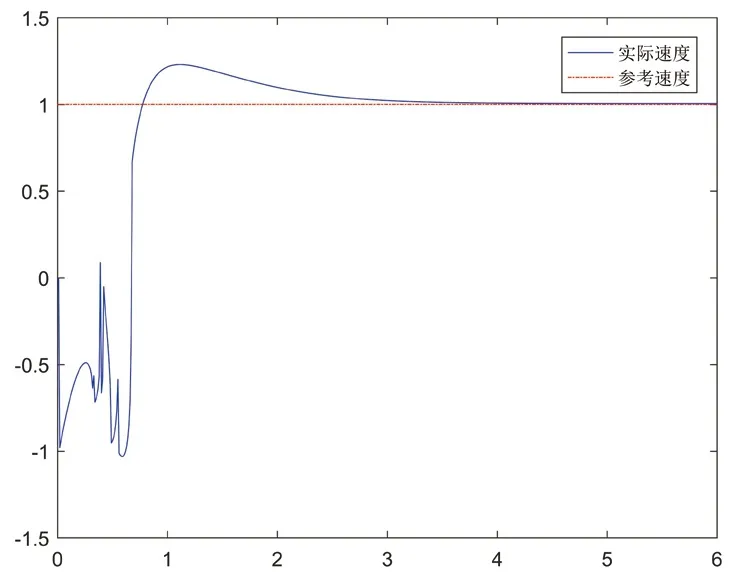
图5 领航者期望速度与实际速度

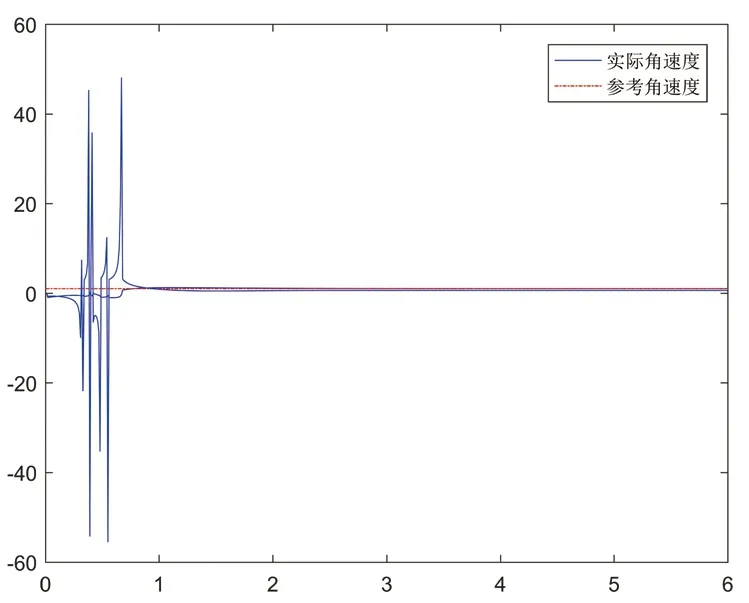
图6 领航者期望角速度与实际角速度

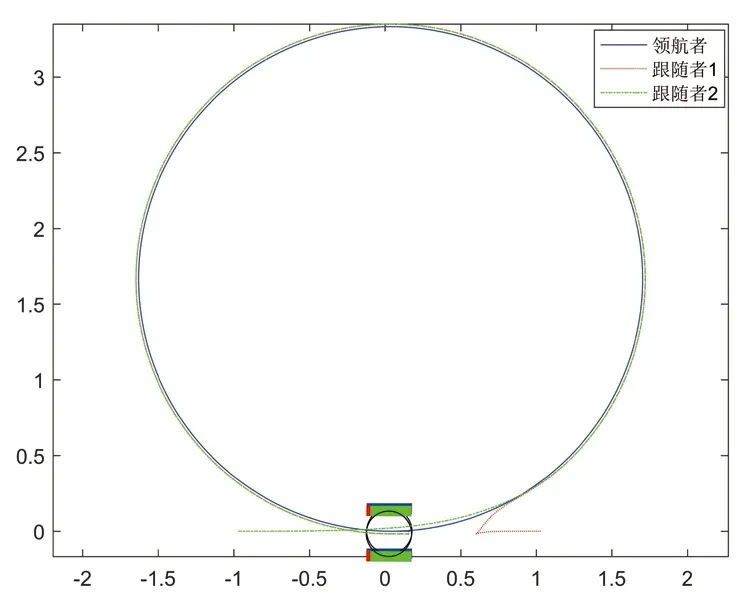
图7 期望误差为零时跟随者轨迹

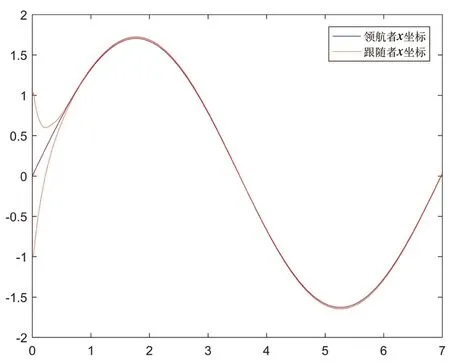
图8 期望误差为零时跟随者x坐标收敛情况

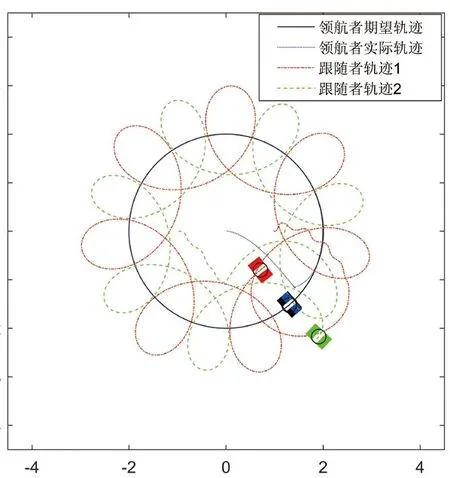
图9 “行星-卫星”式编队效果

7 结 论

本文研究了一种“行星-卫星”式编队方式，即领航者以期望的速度和角速度行驶在规定轨迹上，跟随者保持在领航者坐标系下一特定圆形轨迹上。首先对领航者的轨迹跟踪算法进行了研究，设计了领航者控制器并对其稳定性进行了证明。然后在传统一致性算法基础上，结合人工势能场避障方法，给出了领航者时变情况下的跟随者控制器与稳定性证明。最后通过数值仿真证明了所提算法的有效性。

后续还可围绕文中所提算法进行以下研究：

（1）在实际应用中，当输入达到一定程度时，再增加输入常常不会影响输出的变化，现有算法并未考虑这种输入饱和问题，可以考虑增加饱和限制。

（2）对于很多智能体，速度信息常常难以获得，即使装有速度传感器也可能出现失效等情况，因此可以考虑设计不需要速度信息的控制器，以提高系统鲁棒性。