多重线性回归模型中的最小二乘估计与投影法

袁 敏 智丽萍 高健孙 江 洁

（安徽医科大学卫生管理学院，安徽 合肥 230032）

多重线性回归模型在社会实践中地位举足轻重，特别是在经济问题中，如家庭消费支出受家庭可支配收入、家庭所有的财富、物价水平、金融机构存款利息等多种因素影响。如何探究各影响因素的权重问题，将关系生活决策和幸福指数。因而如何发挥多重线性回归模型在日常生活中的价值，就得从知识的传承开始。多重线性回归模型传统教法是从定义开始，挖掘模型的特性，理论的论证，公式结论的强行记忆，生搬硬套，使得我们的模型价值难以为人们接受。本文将从全新的角度，利用投影法开展多重线性回归模型的研究过程，为我们推广多重线性回归模型揭开新的思路。

一、简单线性回归到多重线性回归:从性别歧视诉讼案谈起

Weisberg（2005）一书的问题6.13中涉及的是美国中西部一所大学在20世纪80年代为“女性工资待遇受歧视”的法律诉讼案所收集的薪水数据（可从R软件的alr3包中的salary数据获得）。该数据包含52个正式教职工的年薪（Salary）及与其相关的 5 个变量，即 Sex（1 ∶女，0：男）；Rank（1∶助理教授 2∶副教授3∶教授）；Year（拥有当前职称的时间，单位：年）；Degree（1：博士 0：硕士）；YSdeg（工龄，单位：年）。

数据表明女性平均工资比男性低3340美元，假设工资的对数服从正态，应用独立两样本t-检验得到p值为0.048，小于0.05，故认为在0.05的检验水平下男性和女性的平均工资有显著的统计学差异。但是，男女性可能存在与工资有关的其它因素（比如职称、学历）的差异，而这些因素可能导致了男女性平均工资的差异，即混杂因素（confounding）。一般职称与薪水是挂钩的，职称越高，平均薪水相对越高，因此我们分别考察男女性的职称分布情况，画出如下条图：

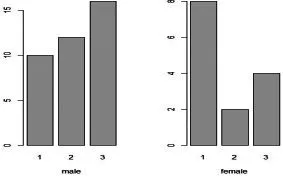
图1.1：salary数据中男性和女性的职称分布条图

从图1.1可以看出，男性和女性在职称组成上有很大的差异，男性中教授职称所占的比例相对较高，而女性职员中助理教授所占的比例较高，因此男女性职员的职称组成差异也许是导致薪水差异的混杂因素。

事实上，独立两样本t检验即建立如下简单线性回归模型(simple linear regression model)：

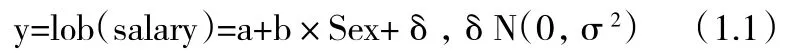
其中Sex取值0，1分别代表女性和男性。独立两样本t检验等价于检验假设H0：b=0。由于薪水可能受其他因素的影响，比如职称等，我们需要在上述简单线性模型(1.1)的右端添加若干项以控制协变量的影响，即建立多重线性回归模型(multiple linear regression model)：

即可达到控制协变量Rank、YSdeg、Degree和Year的目的。在多重线性回归模型中考察薪水是否会与性别有关，即在模型（1.2）下检验假设，相应的p值为0.26〉0.05,说明在控制了其他可能影响薪水的因素前提下，男女的薪水差异没有显著的统计学意义。

一般而言，从简单线性回归模型到多重线性回归模型是为了控制混杂因素，可用下面的流程图直观的表达：

新加项c'z是为了控制z的影响。系数b为给定z的条件下x的效应，所以在多重线性回归模型y=a+bx+c'z+,N（0，σ2）中研究一维随机变量x与y之间的关系可以分成两步进行：

其次将y对x┸进行回归，建立简单线性回归模型y=a+bx┸+即为多重线性回归模型。

二、多重线性回归模型

一般的多重线性回归模型可表达成如下形式和条件：

则模型（2.1）可用矩阵向量形式表达成：Yn×1=Xn×pβp×1+n×1

（1）最小二乘法

假设设计矩阵X为列满秩，为估计参数β,常用的估计方法为最小二乘法（Least Square,LS），即最小化误差平方和：

minβ∈Rp2=minβ∈Rp∑n （y-x'i）2=minβ∈Rp‖Y-Xβ‖2注意到目标函数 Q（β）=‖Y-Xβ‖2=Y'Y-2Y'Xβ+β'X'Xβ，则将函数Q对向量β求导数得到,令0,得到正则方程X（'Y-Xβ）=0。注意到X为列满秩,故X'X可逆。求解这个正则方程,得到LS估计为。进一步计算LS估计的方差为：

下面列举了关于正则方程的几个注解：

注5：当p＞n时，Y=Xβ是一个关于参数β的欠定方程（under-determined system）或称为不定方程。为了求出欠定方程的有意义的解，通常需要施加某些约束条件，比如在数论中限制β为有理数或正整数；比如在压缩感知中限定β为稀疏的，即某一些分量为0，但不知道具体哪些分量为0。如果假设β的p个分量非0，则须解Cnp个适定方程，从得到的Cnp个解中发现满足某些准则的有意义的解或者最优解。

（2）最小二乘法与投影(projection)

投影(projection)是线性代数中的一个重要概念。那么什么是投影呢？形象点说，就是将你需要投影的东西上的每一点向你要投影的平面作垂线，垂线与平面的交点的集合就是投影。图2.1是三维投影中向量b对平面的投影的图示,

图2.1 三维投影

定理2.1minβ‖Y-Xβ‖2等价于其中为Y在L（X）上的投影。

证明：注意到 Xβ=x（1）β1+x（2）β2+…+x（p）βp为 X 各列向量。的线性组合。根据投影的定义，因为与L（X）正交，所以与L（X）中的任何向量Y-u均正交。故。证毕。

三、总结

多重线性回归模型是探索多个协变量与因变量之间关系的一个重要工具。由具体的实例从简单线性回归模型应用中可能带来的问题引入多重线性回归模型有利于激发学生的兴趣，加深学生理解进行多重线性回归的背景。最小二乘法是线性回归模型分析中最经典的估计方法。用投影法讲解最小二乘估计，直观简洁地讲清楚最小二乘法的几何意义，避免了学生死记硬背最小二乘估计的公式以及协方差矩阵的公式。