基于瑞雷波的无损检测理论技术研究

胡杨建，戴圣然，刘虹丹，田裕鹏，黄平，杨颖

(南京航空航天大学 自动化学院，江苏 南京 210016)

0 引言

面波勘探是近几年兴起的一种浅层勘探方法，广泛应用于工程勘探，岩土工程，以及地基评估等方面。在工程物探方法中占据着重要的地位，其原因在于通过所测的面波记录计算出频散曲线就可以直接对波场进行分层，此方法简便、经济、实用。因此，对瑞雷面波的传播规律、机理的认识和准确地提取出频散曲线就显得特别重要。

自1887年Rayleigh发现瑞雷面波之后，大量的学者对各种介质中的瑞雷波传播理论进行了广泛的研究。50年代初，Hsakell对层状介质中的瑞雷面波频散曲线用矩阵方法进行了计算，并且利用天然地震记录的瑞雷波来研究地球内部结构[1]。2001年凡友华在柱坐标下，利用位移应力在各界面处连续及自由表面边界条件导出了层状介质中轴对称柱面瑞雷面波的频散曲线，并进行了数值计算，取得了良好的效果[2]。2008年熊章强等人深入讨论了瑞雷波数值模拟中的边界条件[3]。

总之，虽然前人在瑞雷面波勘探方面已经做了很多实际工作和理论研究，但还有大量的研究工作需要去完成。透彻地了解和认识瑞雷波的振动特点及其传播机理，对其的正演和反演研究具有重要的实际意义，在实际应用中瑞雷面波勘探主要还是以其频散特征为理论基础的。

1 瑞雷波的波场数值模拟

地震数值模拟是用来模拟地震波在底层中传播的一种技术，其目的是在给定一个假定的地层结构后，通过对其正演计算得到理论地震记录。有助于更精细地描绘地质构造，是地震解释的一种有价值的工具。本文主要用交错网格法来实现瑞雷波数值模拟，通过对地震剖面曲线进行了正向填充，将之前交错网格所用的自由边界条件修改为变系数的吸收边界，以防止瑞雷波在边界发生发射来影响其信噪比。

1.1 波动方程及其差分格式

在二维均匀各向同性弹性介质中，质点的振动速度和应力满足以下标量弹性波方程[4]：

(1)

(2)

(3)

(4)

(5)

其中:υx=∂μx/∂t和υz=∂μz/∂t为质点振动速度在x和z方向的分量，μx和uz分别为位移u在x和z方向的分量；τxx和τzz为质点在x和z方向的正应力，τxz为质点在xz平面内剪应力；ρ为介质的密度；μ为介质的剪切模量，λ为拉梅常数。

式(1)-式(5)所示的泛定方程可采用交错网格法进行数值求解[5]，交错网格法所采用的网格剖分方案如图1所示。

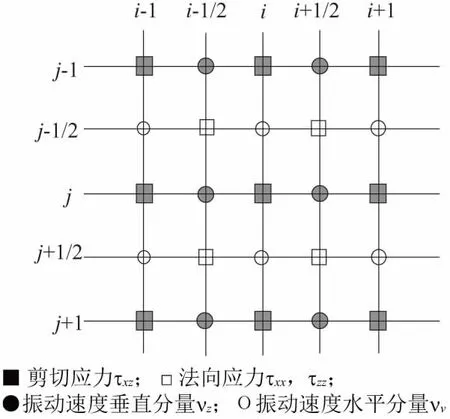
图1 网格剖分方案

分别将νx置于x=i·Δx，z=j·Δz；νz置于x=(i+1/2)Δx,z=(j+1/2)Δz;τxx及τzz置于x=(i+1/2)Δx，z=(j+1/2)Δz;τxx和τzz置于x=(i+1/2)Δx，z=jΔz；τx置于x=iΔx,z=(j+1/2)Δz所对应的离散网格点上。质点振动速度νx，νz及应力τxx，τzz，τxz等变量对于时间的离散采样分别为t=kΔt，t=(k+1/2)Δt，其中Δx，Δz分别为x，z方向的采样间隔；Δt为时间采样率；i=1,2,…N，j=1,2,…,M,N、M为横向、纵向网格点数目；k=1,2,…T,T是时间样点数。则可以得出式(1)-式(5)所对应的数值计算的一阶差商式为：

(6)

(7)

(8)

(9)

(10)

其中:U,V分别为vx,vz的离散量；R，T和H分别为τxx，τzz和τxz的离散量；B为ρ-1的离散量。

1.2 理论均匀半空间模型

模型尺寸为200 m×100 m，其纵横向空间的采样间隔为2 m，时间采样间隔取0.4 ms，均匀半空间纵横波速度和密度为1 500 m/s、840 m/s和2.0 kg/m3。震源位于第75号检波点处，埋深为0 m。模拟可得瑞雷波传播过程中30 ms、60 ms、90 ms和120 ms时间切片效果如图2-图5所示。

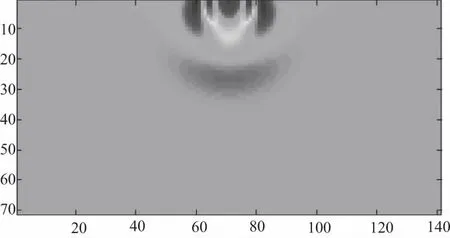
图2 30 ms波场快照

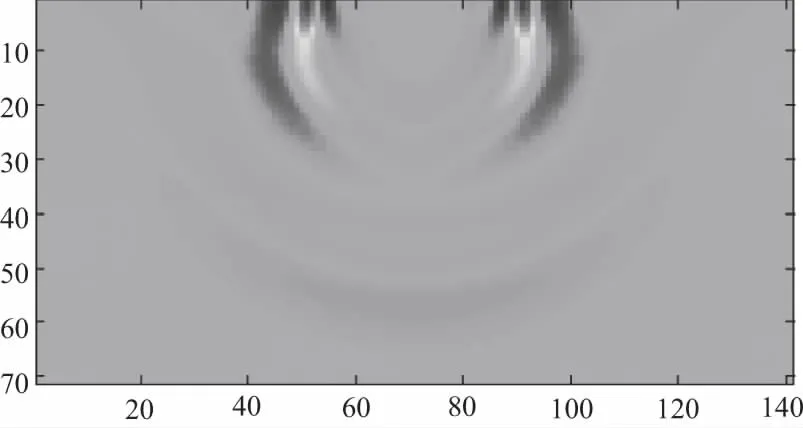
图3 60 ms波场快照

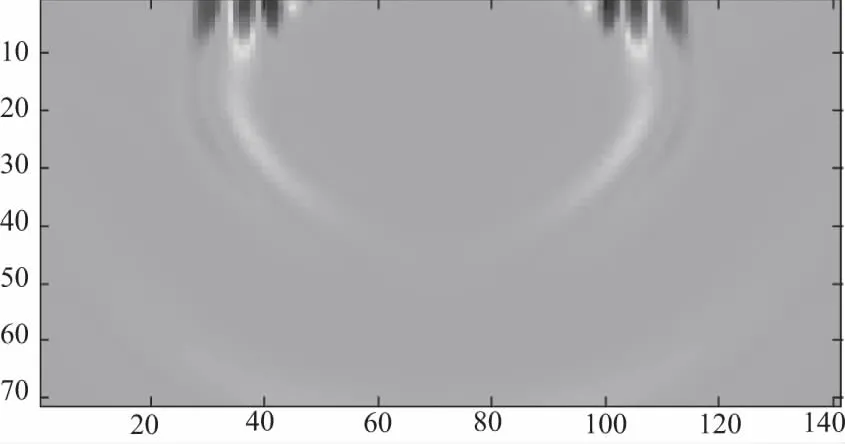
图4 90 ms波场快照

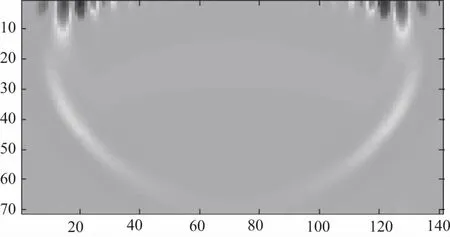
图5 120 ms波场快照

从波场快照图2-图5可以看到明显的瑞雷波波场，且沿着自由界面传播，速度略低于横波速度，其主要能量集中在自由表面，从而可以得到均匀半空间模型单炮合成水平分量和垂直分量记录，如图6所示。在图6中可以看到瑞雷面波是纵波和横波在自由界面处传播时相互干涉而形成的，因此即便在均匀半空间介质中，依然存在很强的瑞雷面波，其能量要强于直达波。

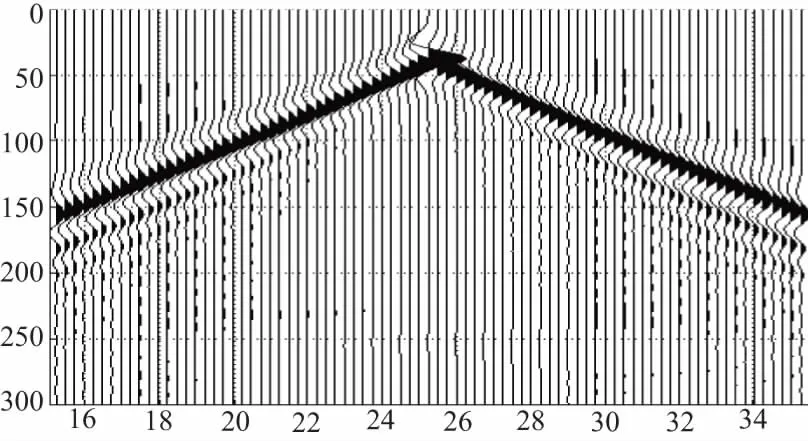
图6 瑞雷波剖面干涉图

通过对上述模型的数值正演模拟，看出可以正演的模拟出各种弹性介质模型中的瑞雷波。还可以得出在均匀半空间中瑞雷波没有出现明显频散现象，且频散特征和地质弹性参数及底层分层结构是密切相关的。同时可以清楚地看到吸收边界对瑞雷波在数值模拟方面的作用，减少了反射波和折射波对传播状态的影响。

2 瑞雷波的反演研究

遗传算法的主要特点是群体搜索策略和群体中个体之间的信息交换，搜索不依赖梯度信息及初始模型的选取，应用瑞雷波的反演计算，通过构建模型及对遗传算法的运用来提高瑞雷波在反演深度方面的精度，以提高瑞雷波在工程探测中的应用与分析。这样不仅解决了瑞雷波频散曲线反演中存在的问题与阻碍，同时也提高了瑞雷波勘探的适用性，推进了瑞雷波勘探的进一步延伸发展。 通过瑞雷波频散曲线非线性反演的研究来进行收敛性分析，成功地解决了传统的局部优化算法依赖初始模拟、不能很好地适应离散问题、非线性问题以及函数关系不能显式表述复杂问题优化的缺陷。

2.1 遗传算法方法与原理

遗传算法的基本思想就是模仿生物界的遗传过程，把最优化问题与生物进化过程加以类比，在实际应用中需要考虑以下因素：编码方式、适应度函数、选择算子、交叉算子和变异算子[6]。

2.2 理论模型

本文的理论模型是在不考虑噪声干扰的情况下，探讨遗传算法在瑞雷波频散曲线反演中的应用情况。设计了1个4层地质模型，利用遗传算法来反演结果。反演的目标函数Φ由实测和理论计算的瑞雷波相速度之均方差RMS(root-mean-square)计算出来[7]，即：

(11)

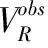
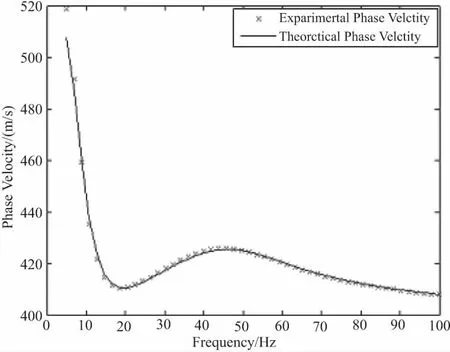
图7 遗传算法反演拟合的频散曲线

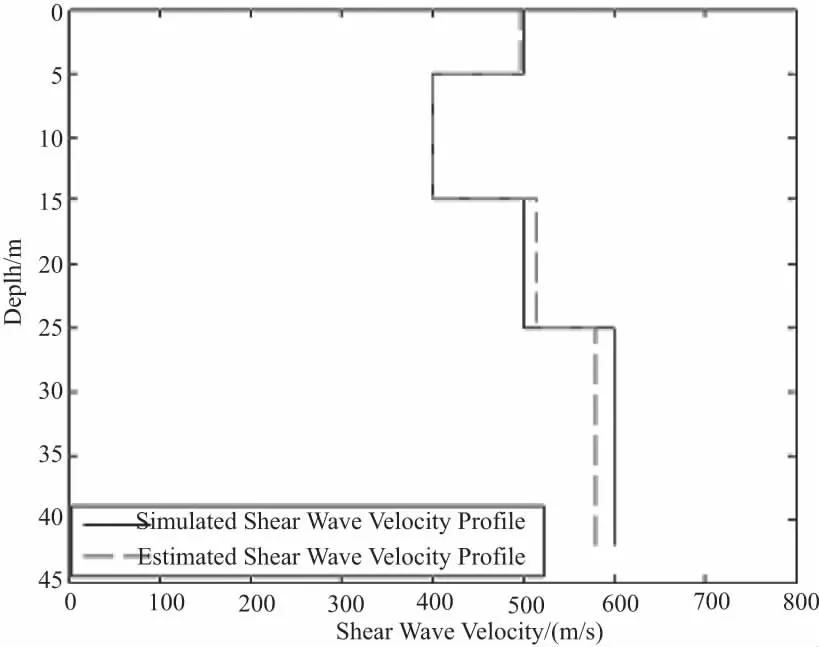
图8 遗传算法反演地质分层与真实模型

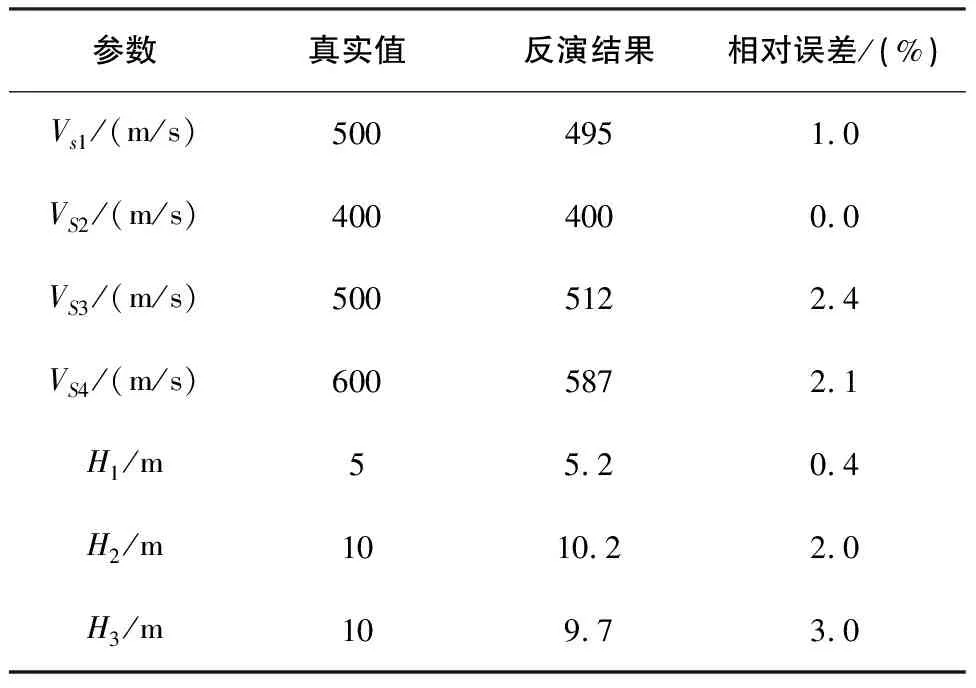
表1 模型遗传算法反演结果

由此可以得出遗传算法在反演方面的有效性和可行性，同时可以看出反演具有非常高的实际意义和研究目的。本章对遗传算法的基本原理进行了介绍，并用1个4层地质模型进行了理论模型的试算，分析了其反演的成果图和误差率，可以得出遗传算法在进行瑞雷波频散曲线非线性反演方面的可行性和优越性，实现了较好的反演结果。

3 结语

瑞雷波的传播特性、频散特性与实际的地质介质紧密相关，所以要深入了解其振动特点以及传播特性，应该从波动方程入手做理论正演模拟。利用弹性波动方程模拟了瑞雷波，并对层状介质做了数值模拟可以得到非常形象的波场快照。然后通过正演作为理论基础，设计1个4层的地质模型，反演出其频散曲线，利用遗传算法对其拟合得出遗传算法在非线性反演方面的优越性和可行性。通过对瑞雷波的理论分析，可以更加了解和认识瑞雷波的本身，在工程探测方面具有更广泛的实际意义。