基于蚁群算法分数阶PID控制器在温度控制系统的应用

刘智城，杨向宇

(华南理工大学 电力学院，广东 广州 510640)

0 引言

生物学家研究发现，蚂蚁在觅食过程中会留下一种分泌物，即信息素，也称外激素。蚂蚁在运动过程中能感知这种物质的存在及其浓度，并进行路径的选择，同时会在所经过的路径上释放信息素。信息素的浓度随时间慢慢挥发，因此在相同时间内，从巢穴到食物源所走的路径越短，信息素残留的浓度就越高，再次被蚂蚁选中的概率就越大。蚁群的集体行为构成了一种学习信息的正反馈机制，即通过个体之间的信息交流与相互协作最终找到最优解。蚁群算法包含两个基本阶段：适应阶段和协作阶段。在适应阶段，各候选解根据积累的信息不断调整自身结构。在协作阶段，候选解之间通过信息交流，以期望产生性能更好的解[1]。

在蚁群优化算法中，一个有限规模的人工蚂蚁群体，可以相互协作地搜索用于解决优化问题的较优解。每只蚂蚁根据问题所给的准则，从被选的初始状态出发，建立一个可行解，或是解的一个组成部分。在建立问题的解决方案时，每只蚂蚁都收集关于问题特征和自身行为规则的信息。蚂蚁既能独立工作，又能共同行动，显示了一种相互协作的行为。它们通过信息素进行信息的交换。每只人工蚂蚁都能够找到一个解，但很可能是较差解。蚁群的所有个体建立起很多不同的解决方案，再通过相互协作找出高质量的解[2]。人工蚂蚁并不试图完全模拟真实的蚂蚁，但其具有真实蚂蚁所没有的能力，如：人工蚂蚁有记忆所经历路径的能力；能够存储蚂蚁过去的信息，以便于携带有用的信息用于生成解决方案的优劣度，控制解决方案。例如，在TSP问题中，利用蚂蚁的记忆，可以将蚂蚁走过的城市置于一个禁忌表中，来禁止蚂蚁重复走过这些城市，进而满足TSP问题的约束条件[1][3]。

在基本蚁群算法中，人工蚂蚁的行为可以描述为：人工蚂蚁通过相互的协作，在所求问题的解中搜索可行解，人工蚂蚁按照人工信息素浓度的大小和基于问题的启发式信息，在问题空间移动来构造可行解。在此，信息素类似于一种分布时的长期记忆，这种记忆全局地分布于整个问题的解空间中。当人工蚂蚁在问题空间中移动时，在经过的路径上留下信息素，这些信息素反映了人工蚂蚁在问题空间觅食过程中的经历[4]。人工蚂蚁在解空间中逐步移动从而构造问题解，同时它们根据解的质量在其路径上留下相应的浓度信息素。蚁群中的其他蚂蚁倾向于沿着信息素浓度大的路径前进，同样蚂蚁在这些路径上留下自己的信息素，从而形成一种正反馈形式的强化学习机制，来指引蚁群找到高质量的问题解。蚁群算法还应包括另外一种机制，即信息素的挥发，蚂蚁走过路径上的信息素随着时间不断挥发，驱使蚂蚁搜索解空间中新的领域，避免求解过程过早地收敛于局部最优解[5]。蚁群算法必须有运行停止标准，即所求解达到预定的条件后，算法停止继续求解。流程图如图1所示，其中NC为迭代次数。

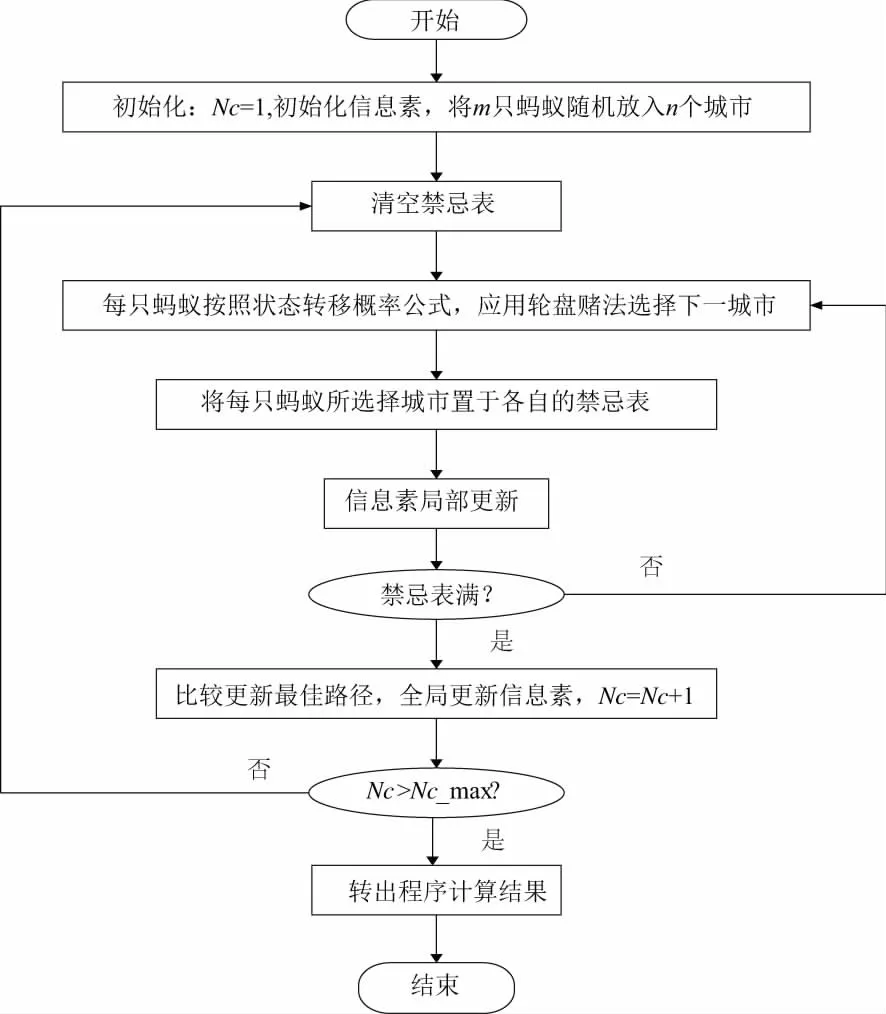
图1 基本蚁群算法流程图

1 蚁群算法PID控制器设计

PID控制器系统的原理图如图2所示。

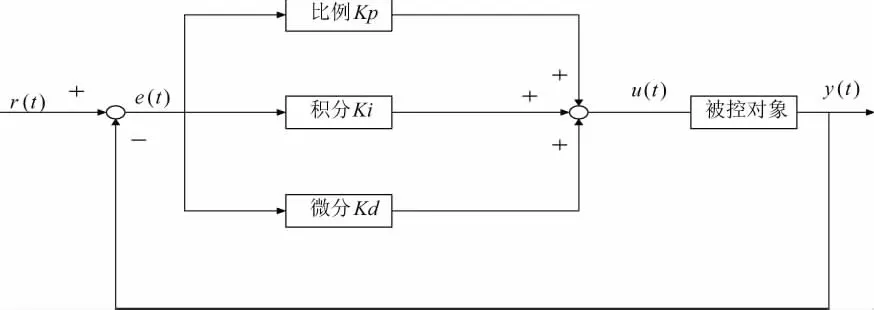
图2 PID控制原理图

其中:r(t)为输入量，u(t)为控制量，y(t)为输出量，e(t)为输入与输出之间的偏差量，即e(t)=r(t)-y(t)。连续时，控制量与偏差量满足：

(1)

离散时，控制量与偏差量满足如下差分方程和增量形式[1]：

(2)

(3)

式中:u(n)为本次控制量，e(n)为本次误差，TI为积分时间常数，TD为微分时间常数，Kp为比例系数，T为采样周期。

在采样周期已知的情况下，PID控制器只有3个参数需要确定，即：Kp、TI和TD，使某一控制性能达到最佳。

蚁群算法优化PID参数的过程：

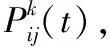
(4)

一次遍历结束后，对每只蚂蚁走过的路径进行评价[6]。首先求得对应的解，求解式为：

(5)

xi=(xiH-xiL)ei+xiL

(6)

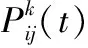
再求取相应的目标函数。然后记录下当前的最佳路径。接下来对各只蚂蚁所经历路径上的信息素进行更新，即:

(7)

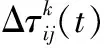
为了加强最佳路径对蚂蚁行为的影响，需要对其信息素进行强化，即：

信息素更新完成后，进入下一次遍历，直到达到最大遍历次数NC为止。最后，输出在历次遍历过程中所选出的最佳路径所对应的解。

蚁群算法寻优简单，鲁棒性强，是一种效率很高的优化算法，它不依赖于数学模型，使处理问题更具有适应性、鲁棒性。

2 分数阶PID控制器设计

对于一些复杂的实际系统，用分数阶微积分建模要比整数阶模型更准确，对于分数阶模型则需要分数阶控制器来提高控制效果。分数阶PID控制器由于多了2个参数，增加了控制的灵活度，对于分数阶系统的控制具有较好的效果，且对于整数阶系统的控制，也具有一定的控制效果[7-8]。

整数阶PID 控制器的传递函数描述为：

(8)

式中：U(s)为控制器的输出；E(s)为控制器的误差输入。将式(8)中的微分和积分项的阶次推广到分数，即可得分数阶PID控制器的传递函数[2]。

(9)

式(9)中，当λ=μ=1时，Gf(s)就变为整数阶PID控制器的传递函数，因此整数阶PID控制器是分数阶PID控制器的特殊形式。分数阶PID所对应的时间域方程可以表示为：

u(t)=Kpe(t)+KiD-λe(t)+KdDμe(t)

(10)

式中D-λ、D-μ为分数阶微分算子。

从式(9)、式(10)可以看出，相比传统PID 3个参数的整定来说，分数阶PID控制器的整定参数有5个，比整数阶控制器多了2个自由度，即：微分器和积分器的阶次，因此分数阶PID更具有灵活性，能更加灵活的控制受控对象，可以得到更好的控制效果[9-10]。

3 仿真与实验

某真空感应炉温度控制系统为二阶惯性环节，其传递函数为：

其中:τ1、τ2为真空感应炉温度控制系统的时间常数，K为控制系统的比例系数。

当τ1=12s、τ2=10s、K=1 000时，其传递函数为：

为获取满意的控制效果，采用时间乘绝对误差积分准则(ITAE)作为目标函数，这种准则能反映控制系统的快速性和精确性，具有较小的超调量和较快的响应速度，即目标函数为：

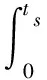
式中，e(t)为系统误差，ts为SIMULINK仿真时间。

蚁群算法中使用的城市个数City=30，路径数Path=10，蚂蚁个数Antsize=40，信息素残留系数取ρ1=0.8，ρ2=1.0，总遍历次数取NC=20。

在应用蚁群算法进行优化时，为了避免所选取参数优化范围过大，考虑实际控制条件限制的前提下，先按经验选取一组较好的参数，然后再根据这组参数确定参数优化范围，利于节约计算量。本案例参数寻优范围为：KP∈[0，120]、KI∈[0，0.1]、Kd∈[0，0.1]、λ∈[0，1]、μ∈[0，1]。由于蚂蚁路径的选取是以随机概率选取的，因此每次运行的结果都不一样，有差异，可多运行几次，选取控制效果最好的一组参数作为寻优结果。

PID控制器优化参数为：KP=110.771 2、KI=0.038 35、Kd=0.011 844，最优参数所对应的目标函数值为：J=1.53×10-6。

分数阶PID控制器优化参数为：KP=119.927 5、KI=0.065 5、Kd=0.032，λ=0.462、μ=0.145 5，最优参数所对应的目标函数值为：J=1.229 3×10-6。

采用优化整定后的PID控制阶跃响应和分数阶PID控制阶跃响应对比图如图3所示。

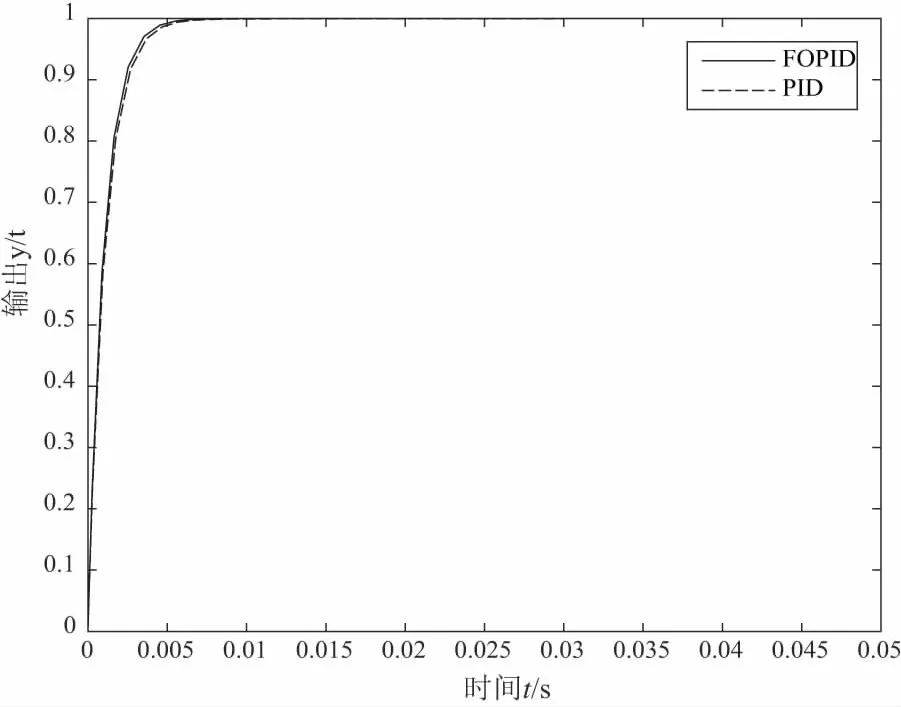
图3 PID控制和分数阶PID控制阶跃响应对比图

在0.025s～0.03s加入干扰信号后，采用优化整定后的PID控制阶跃响应和分数阶PID控制阶跃响应的对比图如图4所示。

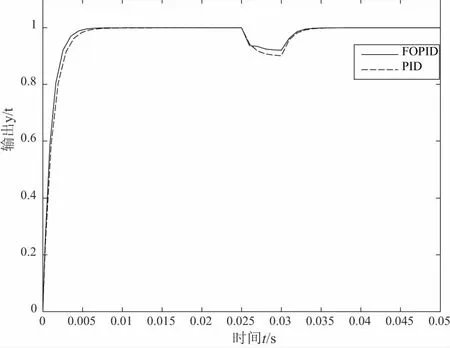
图4 干扰影响下的PID控制和分数阶PID控制阶跃响应对比图

由图3-图4可知(黑白印刷有疑问可咨询作者)，基于蚁群算法优化后，PID控制阶跃响应无超调，调节时间短，响应速度快；相比PID控制，分数阶PID控制阶跃响应无超调，调节时间更短，响应速度更快，目标函数的值更小。有干扰的情况下，相比PID控制，分数阶PID控制的抗干扰能力更强，鲁棒性更好。

4 结语

通过仿真分析对比可知，基于蚁群算法优化的整数阶PID控制器比传统PID控制器具有更优的性能；基于蚁群算法优化的分数阶PID控制器相对于基于蚁群算法优化的整数阶PID控制器具有更短的调节时间，也没有超调，且响应速度更快。