基于均匀化理论分析磁流变弹性体(MR)磁致剪切模量
2018-11-02,,,
, ,,
(1.塔里木大学 机械电气化工程学院,新疆 阿拉尔 843300; 2.兰州大学 土木工程与力学学院,甘肃 兰州 730000)
1 前 言
磁流变弹性体(MR弹性体)是一种新型智能材料,在外磁场作用下力学性能会显著增强[1],对这类效应开展研究已成为关注的重点[2]。在对磁流变弹性体各项性能的研究中,磁流变弹性体的剪切力学性能,特别是垂直于铁磁颗粒形成链方向的剪切方向的力学性能,一直都是研究的焦点[3]。
磁流变弹性体磁致剪切模量的理论预测,通常选用磁偶极子理论[4-5]。磁偶极子理论,即在外加磁场作用下,将每一个磁化的铁磁颗粒都当做一个单独的磁偶极子来处理;之后计算在外磁场作用下铁磁颗粒间的相互作用能和磁能密度,进一步处理后就可得到外场作用下同一条链上铁磁颗粒间的相互作用[6-8]。Furst与Gast[9]在计算磁场强度时,充分考虑了同一条链上铁磁颗粒间的相互作用,使得计算得到的磁场强度大为精确,最后通过能量变分求得磁致剪切模量。Shen等人[10]在此基础上,进一步完善了此磁偶极子耦合模型,较为精细地预测了磁致剪切模量。以上这些人都是在磁偶极子模型的基础上进行的研究。但磁偶极子模型在推导过程中,没有考虑基体材料性能、基体变形能与颗粒磁能间相互作用等因素;且对于颗粒间距很小的情况,磁偶极子模型也没有考虑到颗粒非线性磁化、磁偶极子与外场的关系等问题[11]。
故此,需在研究磁流变弹性体的磁致剪切模量之前,先对在外加磁场作用下磁流变弹性体内磁场的分布进行深入研究。对磁流变弹性体内磁场的求解可选取多种算法,其中运用最广泛的就是均匀化理论。基于均匀化理论的主要算法有:Maxwell推测法[12]、Rayleigh-Lam推测法[13-14]、Hashin-Shtrikman边界法等[15]。Yin等[16-17]在Mura[18]等人的细观力学研究基础上,运用均匀化理论计算磁流变弹性体内颗粒与基体上的平均的磁场分布。运用这种方法计算出来的磁场,在考虑铁磁颗粒间相互作用的基础上,进一步得到颗粒与基体之间磁场的相互影响,对研究磁流变弹性体内的磁致力学性能有重要意义。但由于在求解过程中进行了一定程度的简化与近似,故所得到的磁场分布与实际情况存在一定的差距。
本研究运用均匀化理论计算在外加磁场作用下磁流变弹性体内颗粒与基体的磁场分布,并求解磁流变弹性体内的各种能量密度,之后再分析含有链状结构的磁流变弹性体的磁致剪切模量。最后将计算结果与偶极子方法在相同条件下得到的结果进行对比,并将两者间的差异进行分析、总结。
2 基于均匀化理论计算基体与颗粒磁场相互作用下的磁致剪切模量
2.1 基于均匀化理论计算磁流变弹性体内基体和颗粒相互作用下的磁场分布
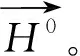
(1)
(2)
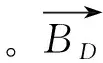
(3)
将(1)、(2)、(3)三式联立,可得磁流变弹性体内的颗粒平均场与基体平均场分别为:
(4)
(5)
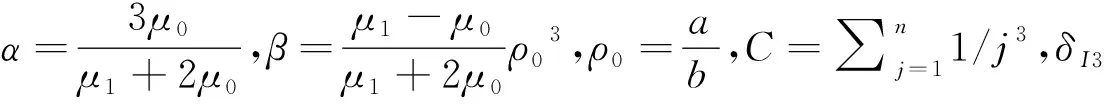

(6)
则β变为β′:

图1 (a)加剪力前、(b)加剪力后磁流变弹性体内铁磁颗粒链的变化Fig.1 Variation of ferromagnetic particle chains in magnetorheological elastomers before shear stress imposed (a) and after shear stress imposed (b)
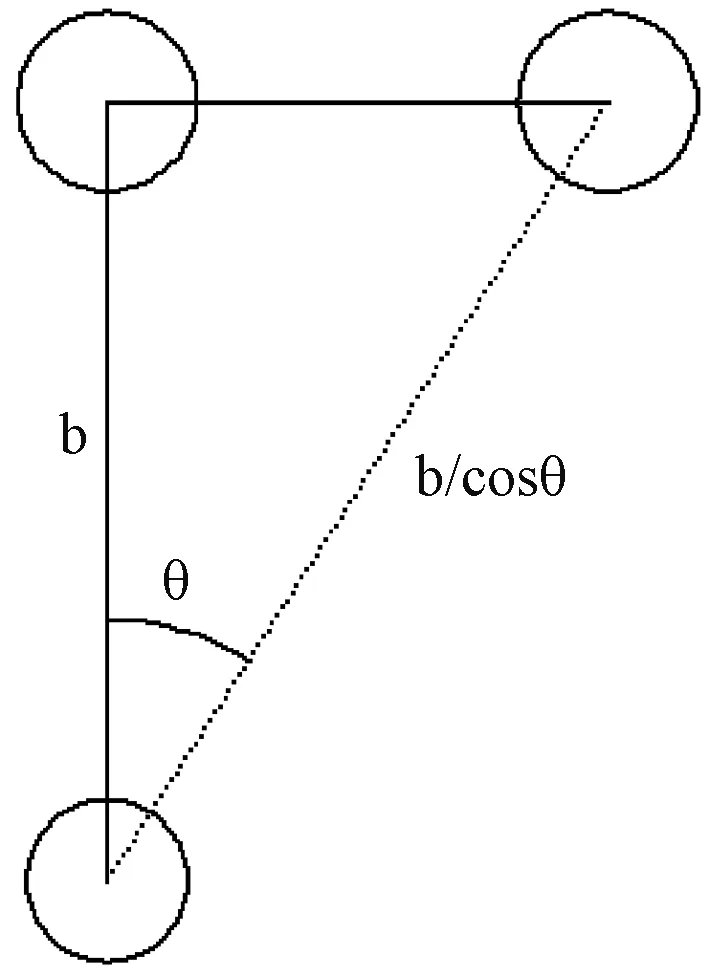
图2 磁流变弹性体内剪应变与铁磁颗粒的关系图Fig.2 Relationship between shear strain and ferromagnetic particle in magnetorheological elastomer
(7)
此时整体的磁场分布为:
(8)
(9)
2.2 基于均匀化理论计算磁流变弹性体内的磁致剪切模量
在单一方向均匀磁化作用下,可忽略磁畴内的交换能与磁晶各向异性能。由于选取的材料不是磁致伸缩材料,故认为磁致伸缩效应的影响远小于磁致剪切效应的影响,从而又可以忽略磁晶应变能。此时颗粒内总的磁能密度为静磁能,设为ωα:
(10)
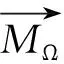
(11)
设磁流变弹性体内整体的平均磁能密度为ω,则有:
(12)
设磁流变弹性体内整体的平均磁致剪切模量为ΔG。在均匀材料内,假设只有剪应变,则磁致剪切模量可表示为磁能密度对剪应变的二阶导。故平均磁致剪切模量ΔG为:
(13)

(14)

(15)
(16)
3 均匀化方法、磁偶极子理论各自算结果与实验数据的对比及分析
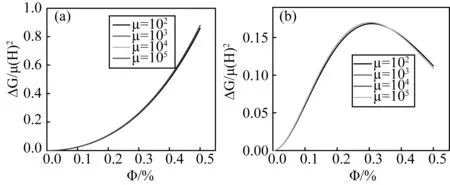
图3 不同方法获得的相对磁致剪切模量与颗粒体积分数的关系(a) 磁偶极子法; (b) 均匀化方法Fig.3 Curves of relative magnetic shear modulus and particle volume fraction obtained by different methods (a) magnetic dipole method; (b) homogenization method
图3为在磁导率μ分别为μ=102、μ=103、μ=104、μ=105时,相对磁致剪切模量ΔG/μ0(H0)2与颗粒体积分数φ的关系图,这是由于磁流变弹性体中的颗粒为铁磁颗粒,而铁磁体的磁导率一般在102~105之间。由图3(a)可知,采用磁偶极子方法获得的相对磁致剪切模量ΔG/μ0(H0)2随着颗粒体积分数φ的增加而持续增加,且四种磁导率下对应的四条相对磁致剪切模量与颗粒体积分数φ的关系曲线重合为一条曲线。由图3(b)可知,基于均匀化理论获得的相对磁致剪切模量ΔG/μ0(H0)2随着颗粒体积分数φ的增加呈现先增加后减小的趋势,最后趋于稳定,且四种磁导率下对应的磁致剪切模量与颗粒体积分数φ的关系曲线的变化趋势一致。
对比图3(a)与图3(b)可知,其共同之处为:在不同颗粒磁导率μ作用下,各曲线间的相对磁致剪切模量ΔG/μ0(H0)2变化不大;当颗粒体积分数φ≤30%时,两者的相对磁致剪切模量都随颗粒体积分数φ的增加而增大。两者的不同之处:当颗粒体积分数φ≥30%时,磁偶极子方法获得相对的磁致剪切模量持续增大,而均匀化方法获得相对的磁致剪切模量出现拐点,具有最大值,且两者在数值上相差较大。

图4 不同方法获得的磁致剪切模量与磁感应强度关系曲线Fig.4 Curves of magnetic shear modulus and magnetic flux density obtained by different methods: magnetic dipole method, homogenization method and experiment method
M.Lokander[20]使用丁腈橡胶作为基体,微米级不规则形状的纯铁颗粒作为填充颗粒,在无场条件下,制备含不同体积分数纯铁颗粒的磁流变弹性体试样。之后测试在磁饱和状态(0.8T)下,含不同体积分数磁流变弹性体试样的磁致剪切模量。依据实验,在B=0.8T,μ=103,γ=0.1条件下,获得ΔG%~φ的曲线图(ΔG%为磁致剪切模量ΔG和基体剪切模量G的比值,试验中认为基体剪切模量G为常数,取G=12MPa)。如图5所示,磁偶极子方法所得ΔG%随着颗粒体积分数φ的增大而持续增加,并在φ=30%之后大于实验值,与实验数据吻合较差;而基于均匀化方法所得ΔG%随着颗粒体积分数φ的增大而增大,并在φ=30%处达到最大值,且与实验数据较为接近。当φ≥30%时,ΔG%明显小于实验数据,这是由于颗粒体积分数φ≥30%时,不同铁磁颗粒链之间的间距会减小,需要考虑不同颗粒链间相互作用的影响,而文中只考虑了同一条颗粒链间的作用。

图5 不同方法获得的磁致剪切模量与颗粒体积分数的关系曲线Fig.5 Curves of magnetic shear modulus and particle volume fraction obtained by different methods: magnetic dipole method, homogenization method and experiment method
磁流变弹性体的磁场分布,除铁磁颗粒间的相互作用外,还需考虑颗粒与基体之间磁场的相互影响。本文基于均匀化理论计算磁流变弹性体的磁致剪切模量,并与磁偶极子模型在相同条件下计算出来的结果以及实验数据进行对比。具体结论如下:
1.由图3可知,磁流变弹性体中的填充物为铁磁颗粒时,颗粒磁导率的变化对磁致剪切模量的影响不大。
2.当颗粒体积分数小于 30%时,均匀化方法与磁偶极子理论两者得到的磁致剪切模量都随颗粒体积分数的增加而增大,且两者的结果与实验数据都比较接近。
3.当颗粒体积分数增加到30%时,基于均匀化理论得到的磁致剪切模量出现最大值,其整体变化规律与实验结果基本吻合,可以预测磁致剪切模量最大时的颗粒体积分数。
4.基于磁偶极子理论计算的磁致剪切模量随颗粒体积分数的增加而持续增加,不会出现最大值,且当颗粒体积分数大于 30%时,与实验结果吻合度较差。
