列车可修系统的可靠性分析与评估

张荧驿 傅振亮 田雪艳 谈立成

(中车唐山机车车辆有限公司，063035，唐山//第一作者，工程师)

可靠性增长数据分析是通过收集产品的可靠性数据，不断动态地分析与评价产品可靠性水平的过程。可修系统是可通过修复性维修恢复其全部功能的产品。可修系统的相邻故障间隔通常不是独立同分布的，而非齐次泊松过程(NHPP)模型一般用来分析既不独立也不同分布的随机变量[1]；幂律过程(PLP)模型(或AMSAA模型)是NHPP模型的一种，常被用于描述复杂系统的可靠性模型增长和可修系统的可靠性分析与评估，有着非常广泛的应用。

1 随机过程模型

1.1 NHPP模型

如果一个计数过程{N(t),t≥0}满足以下3个条件，则称该过程为NHPP[1]：

(1)N(0)=0；

(2) {N(t),t≥0}具有独立增量性，即在任意不相重叠的两个区间内，时间发生的次数相互独立；

Pr{N(t2)-N(t1)=k}=

(1)

当Λ(t)=bt时，NHPP减弱为齐次泊松过程(HPP)。

式中：

N(t)——故障次数函数；

k——故障次数；

λ(t)——故障率函数或强度函数；

b——故障率。

1.2 幂律过程模型

当Λ(t)具有以下强度函数时，称为PLP模型：

λ(t)=bβtβ-1

(2)

式中：

β——形状参数或增长参数。

当使用极大似然估计法时，PLP模型也称为AMSAA模型。因其强度函数λ(t)与Weibull分布的概率密度函数相似，因此，PLP又称为Weibull过程[2]。

对于AMSAA模型，当0<β<1时，系统处于可靠性增长趋势；当β>1时，系统处于可靠性下降趋势；当β=1时，Λ(t)=bt，PLP就退化为HPP[3]。

2 检验和评估

2.1 拟合优度检验

采用拟合优度检验确定故障数据是否符合AMSAA模型[3]。

Cramer-Von Mises检验统计量为：

(3)

对于定数截尾型数据，

(4)

对于定时截尾型数据，

(5)

式中：

M——相邻故障时间间隔的个数；

T——定时截尾时间。

2.2 参数估计

对于完全样本的概率密度函数，对于未知参数θ1,θ2,…,θk的极大似然函数可表示为：

(6)

对极大似然函数取对数，分别对θ1,θ2,…,θk求偏导数，令其等于0，即可得到各参数的估计值。

一般情况下，使用的数据往往存在部分缺失，称为删失数据。对于单侧删失(定时截尾)数据，极大似然函数修订公式为：

(7)

其中，[R(t*)]n-k为n-k个删失单元在截断时刻不发生故障的概率。对于定数截尾的数据，t*被替换为tn。

二参数威布尔分布的极大似然估计对于完全和单侧删失的数据，形状参数β的估计公式如下[4]：

(8)

因此，得到参数β、b的极大似然估计值为：

对于定数截尾型数据，

(9)

式中：

对于定时截尾型数据，

(10)

2.3 趋势检验

采用Laplace分析法对数据进行趋势检验，验证产品的可靠性是否存在变化，以确定改进措施是否有效。

单台或多台系统的定数截尾或定时截尾型数据的Laplace检验可按如下步骤进行[3]。

第一步：建立假设。

原假设H0：单台系统(或多台系统)的故障数据服从HPP。

备择假设H11：相邻故障时间间隔M随机地变长。这意味着产品可靠性在增长。

备择假设H12：相邻故障时间间隔M随机地变短。这意味着产品可靠性在下降。

第二步：选取检验统计量μ。

对于定数截尾型数据，

(11)

对于定时截尾型数据，

(12)

第三步：根据数据计算μ的值。

第四步：根据规定的检验显著性水平α，确定拒绝域。

无论定数截尾还是定时截尾，显著性水平α和相邻时间间隔数M的拒绝域是相同的。

在H0对H11的检验问题中，拒绝域W1={μ<μα}。

在H0对H12的检验问题中，拒绝域W2={μ>μ1-α}。

而在H0对H1=H11∪H12的检验问题中，拒绝域W={μ>μ1-α/2}∪{μ<μα/2}。

其中，μα/2<μ<μ1-α/2，其值依赖于M，可查表得到。

第五步：将μ的值与μ1-α/2、μα/2比较，做出判断。

当μα/2<μ<μ1-α/2时，接受H0，表示相邻故障时间间隔服从指数分布，产品的可靠性没有变化趋势；

当μ<μα时，拒绝H0，接受H11，可靠性有显著增长趋势；

当μ>μ1-α时，拒绝H0，接受H12，可靠性有显著下降趋势。

2.4 可靠性参数评估

可修系统往往是“修复如旧”的，可靠性水平会随时间而改变。

针对产品的特性以及对该产品的要求选择合适的参数以体现产品的可靠性，如平均故障次数E[N(t)]、平均首次故障时间tE[N(t)]=1、瞬时平均故障间隔时间tIMDBF和累积平均故障间隔时间tCMDBF[2,5-7]。公式如下：

(13)

E[N(t)]表示在(0,t]时间内系统的平均故障次数。

(14)

tE[N(t)]=1是描述可修系统首次故障状况的一个可靠性特征量，相当于不可修产品的寿命问题。

(15)

tIMDBF表示任意t>0时刻的平均故障间隔时间(tMDBF)，反映在(t，t+Δt)时间段内系统当前的移动平均可靠性水平。

(16)

tCMDBF表示在(0，t)时间段内累积的tMDBF，反映系统在时间段内总体的可靠性水平。

3 工程实例

截止2012年，某列车受电弓系统在运营过程中共发生了351次故障，首先对运营数据进行了预处理，规则如下：

(1) 本案例中受电弓的序列号记录不完善，不能使用产品的序列号进行产品评估数据处理。由于受电弓安装在不同车辆上，因此可将受电弓所在车辆的编号作为唯一标识，以此将一辆车上的受电弓作为一个系统。

(2) 受电弓故障时，有时需要通过原位修理或更换零部件进行恢复，将原位修理或更换零部件看作是“修复如旧”，当作同一个系统；有时则需要更换整个受电弓才能恢复，将更换整个受电弓看作“修复如新”，当作新的系统。

(3) 将运营期间受电弓经历的无原因更换和技术整改更换看作是预防维修，并且针对受电弓维修(包括更换)情况进行的分析都基于现有的预防维修。

(4) 在工程应用中，不同产品的可靠性的衡量指标不一样，可靠性分析公式中的t既可以代表时间，也可以代表里程、循环次数。列车以运营里程作为考核指标，因此，本文将运营里程代入可靠性公式中的t，进行相关可靠性计算与分析。

受电弓处理后的数据分属298个系统，可将这些数据看作定数截尾型数据，见表1。

表1 某型受电弓定数截尾数据

3.1 拟合优度检验

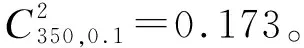
3.2 参数估计

将故障数据代入式(8)和式(9)，可得β、b的极大似然估计值为：

3.3 趋势检验

将M=n-1=350，故障数据代入式(11)，计算趋势检验统计量μ=-32.59。

取α=0.1，可得μα/2=-1.645。由于μ<μα/2，表明此型受电弓具有增长的趋势，显著性水平为α/2=0.05。

3.4 可靠性参数评估

上述可靠性参数的表达式如下：

当列车运行1年(约80万km)时，受电弓的E[N(t)]为:

次

受电弓的平均首次故障里程tE[N(t)]=1为:

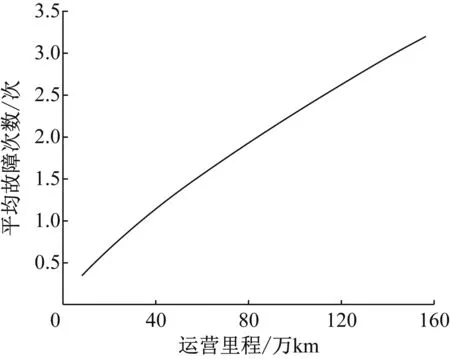
图1 受电弓平均故障次数随运营里程变化情况

图2 受电弓平均故障间隔里程随运营里程变化情况

受电弓的平均故障间隔里程呈上升趋势(β<1)。由于tCMDBF累积了低水平的tMDBF，所以tIMDBF比tCMDBF上升得更快。受电弓平均首次故障里程(tN(t)=1)约为33.57万km。按年运行80万km计算，第一年将出现1.91次故障，若维修保养得当，则以后的故障次数将逐年减少。

4 结语

本文研究了一种可修系统的可靠性评估方法，具体给出了随机过程模型的选取、拟合优度检验、参数估计、趋势检验和可靠性参数评估方法。最后给出了一个工程实例，结果表明某列车受电弓的运营数据服从AMSAA模型，tMDBF呈上升趋势(β<1)，随着对受电弓的维修，其总体可靠性基本稳定，并略有提高。该方法具有很强的借鉴意义，可以应用到列车其他关键可修系统的可靠性分析与评估中。