GPS辅助MIMU静止条件下的初始对准方法
2018-11-01张复建王跃钢腾红磊
张复建 单 斌 王跃钢 杨 波 腾红磊
火箭军工程大学导弹工程学院,西安710025
传统的高精度惯性器件在捷联惯性导航系统(SINS)中难以广泛应用的最大因素是其成本和重量,随着微机电系统(MEMS)技术的不断发展,基于微机电技术的微型陀螺仪和加速度因具有成本低、功耗低和体积小等优势,在民用和军事方面,都应用的越来越广泛[1]。
然而,低成本的微型惯性测量单元(MIMU,简称:微惯组),由于受微机电技术工艺等所限,微惯组的输出具有较大的偏差和噪声[2],其测量精度相对传统的惯性器件低很多,尤其是陀螺仪在静止状态时,无法敏感地球自转角速率,因此,微惯组无法使用双矢量法完成初始对准,必须依靠外部测量信息进行辅助对准。随着全球卫星定位系统(GPS)的不断发展,李士心[3]采用GPS提供的速度信息辅助低成本的IMU/GPS组合导航系统进行初始对准,较好地估计了航向角误差和IMU参数误差,庞春雷[4]针对低精度的捷联惯性导航无法实现航向角的自对准和GPS双天线侧向需要较长时间初始化的问题,研究了二者相互辅助的算法,同时,许多学者研究了GPS测量姿态角的方法[5-6],对此,本文通过GPS测量航向角,融合加速度计输出信息,实现粗对准过程,采用改进的自适应卡尔曼滤波方法实现精对准过程。
1 静基座粗对准
1.1 常用坐标系及转换关系

(1)
式中:c表示余弦函数;s表示正弦函数。
当采用四元数[q0,q1,q2,q3]T表示姿态矩阵时,其对应关系为[7]:
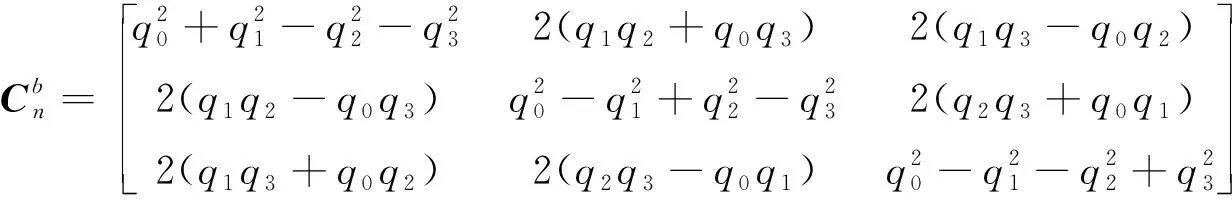
(2)
姿态角与四元数的转换关系为:
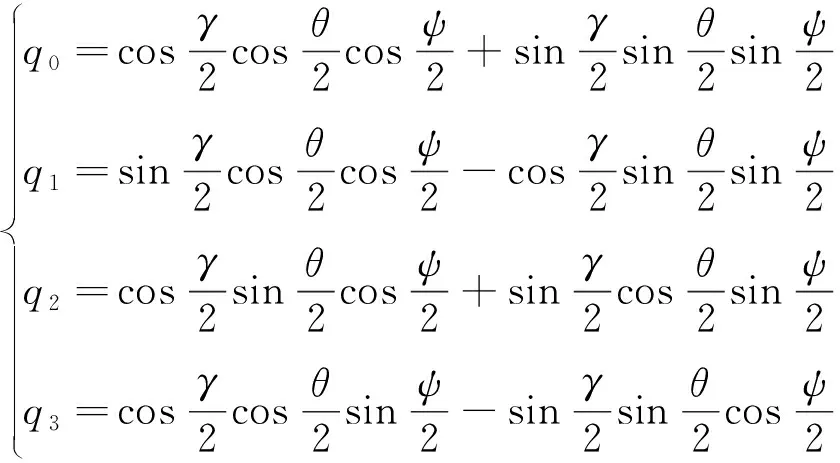
(3)
1.2 粗对准原理
当载体处于静止状态时,加速度计输出为载体重力矢量在载体系的投影:
(4)
式中,g为重力加速度,式(4)单位化后得到:
(5)
将式(2)带入(5)并整理得到:
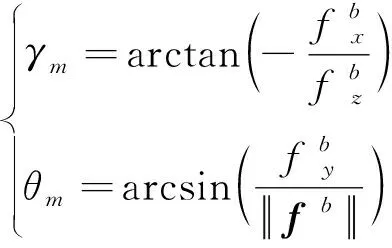
(6)
因此,可通过加速度计输出计算载体的水平姿态角θm和γm。
同时,利用GPS双天线测向原理[8],可输出载体的航向角ψm。按照式(1)计算姿态矩阵,完成粗对准过程。值得注意的是,在粗对准过程中,通过GPS多次测量取平均值的方式,可以精确得到载体的纬度L。
2 静基座精对准
在粗对准阶段,由于加速度计存在零偏误差,影响水平姿态角的计算精度,GPS双天线测向得到的航向角误差,影响粗对准得到的姿态矩阵的准确。本文通过采用卡尔曼滤波方法,在粗对准基础上,滤除噪声误差影响,进一步估计得到载体的高精度姿态矩阵,完成精对准过程。载体的对准流程如图1。
图1 初始对准流程
2.1 系统状态方程
采用四元数作为精对准系统的状态量,四元数的微分方程如下:
(7)
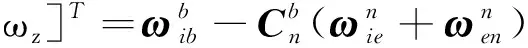
惯性元件(MIMU)的量测误差较大,降低了系统整体初始对准精度,与加速度计误差相比,陀螺仪漂移误差对系统初始对准性能的影响更大,因此,将陀螺仪的常值漂移误差状态列入系统状态量中,对应模型[9]表示如下:
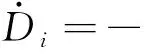
(8)
式中,D表示陀螺仪常值漂移误差;w(t) 表示白噪声;β和σ分别为马尔科夫过程的相关系数和驱动白噪声的标准方差。
选取系统状态变量如下:
x=[q0,q1,q2,q3,Dx,Dy,Dz]T
(9)
由式(7)和(9)建立系统的状态微分方程:
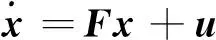
(10)
离散化后得到:
xk+1=Φkxk+Gkwk
(11)
式中,Φk为状态转移矩阵;Gk为系统噪声分配矩阵;wk为系统噪声,满足wk~N(0,Qk)。
2.2 系统量测方程
载体的水平姿态角θm和γm由加速度计输出计算得到,航向角ψm由GPS提供,可根据式(3)得到量测四元数如下:
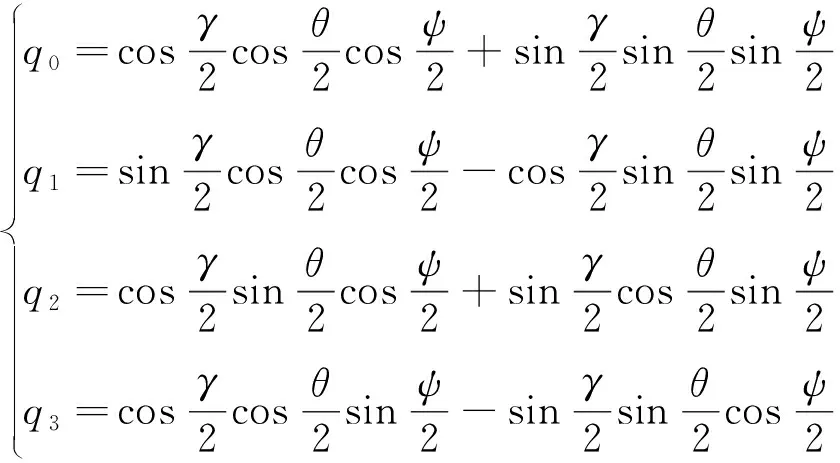
(12)
定义系统观测量为:
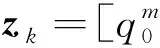
(13)
式中,上标m表示对应变量为量测值。则系统的量测方程表示为:
zk=Hkxk+vk
(14)
式中,观测矩阵Hk=I4,vk为观测噪声,满足vk~N(0,Rk),且与系统噪声wk不相关。
2.3 卡尔曼滤波算法
经典的卡尔曼滤波算法以线性最小方差为估计原则,通过量测值按一定递推算法实现状态向量的估计,其算法过程如下:
1)初始化:
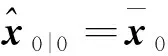
(15)
2)时间更新:
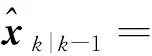
(16)
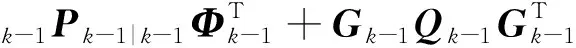
(17)
3)量测更新:
(18)
(19)
(20)
3 改进的自适应滤波算法
传统的卡尔曼滤波算法,滤波效果取决于系统准确的先验统计知识,包括系统噪声矩阵Q和观测噪声矩阵R,因此,当噪声统计特性不准确或者可变时,直接影响滤波效果。针对此情况,经典卡尔曼滤波的基础上,依据量测新息和状态残差,自适应的在线调整噪声矩阵,实现对状态量的精准估计。
3.1 自适应的系统噪声估计
(21)
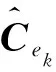
(22)
式中,j0=k-N+1,N表示采样点的数目,采用估计的新息协方差替换其理论协方差得到:
(23)
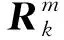
(24)
式中,LR为移动窗口的大小。
3.2 自适应的观测噪声估计
定义状态残差为:
(25)
状态残差dk表示状态向量估计值在量测更新前与更新后的差别,大的状态残差表明状态的一步预测误差较大,当采用新的量测新息更新状态估计值时,会出现大的估计跳跃现象。为了提高算法的预测性能,应对状态残差作适当修正,类似于观测噪声,系统噪声修正如下:
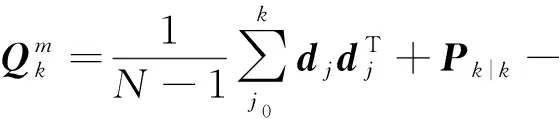
(26)
(27)
式中,LQ为移动窗口的大小。
4 仿真实验

为有效验证本文对准方法,在上述条件下,设置4组实验分别为:
实验1:θ=γ=5°,ψ=40°;
实验2:θ=γ=10°,ψ=40°;
实验3:θ=γ=20°,ψ=40°;
实验4:θ=γ=30°,ψ=40°。
仿真时间设置400s,前120s为粗对准过程,根据粗对准过程的结果,完成精对准过程中卡尔曼滤波器的初始化,120s之后切换为精对准过程。
上述实验中,当微惯组静止时,基于加速度计解算的水平姿态角,由于受到加速度计误差的影响,水平姿态角误差较大,且波动幅度变化剧烈。为便于合理掌握精对准过程中量测噪声统计特性,将粗对准过程中所测量的姿态角数据序列的平均值视为姿态角真实值,并转换为对应四元数序列,将对应四元数误差的方差视为量测噪声统计特性。
从4组实验得出的结论是:
1)采用改进的自适应卡尔曼滤波方式能有效降低对准的姿态误差,俯仰角误差从20′基本降到5′之内,航向角误差从60′基本降到20′之内;
2)虽然采用滤波算法能有效降低横滚角误差,但是,针对不同横滚角状态,其滤波效果不如俯仰角误差及航向角误差,且随着水平姿态角的增大,对应的横滚角对准误差均值逐渐增大,其误差波动范围也有增大的趋势;
3)为了能得到较好的初始对准结果,应当尽量保证载体处于小角度的水平状态。
图2 俯仰角误差
图3 横滚角误差

图4 航向角误差
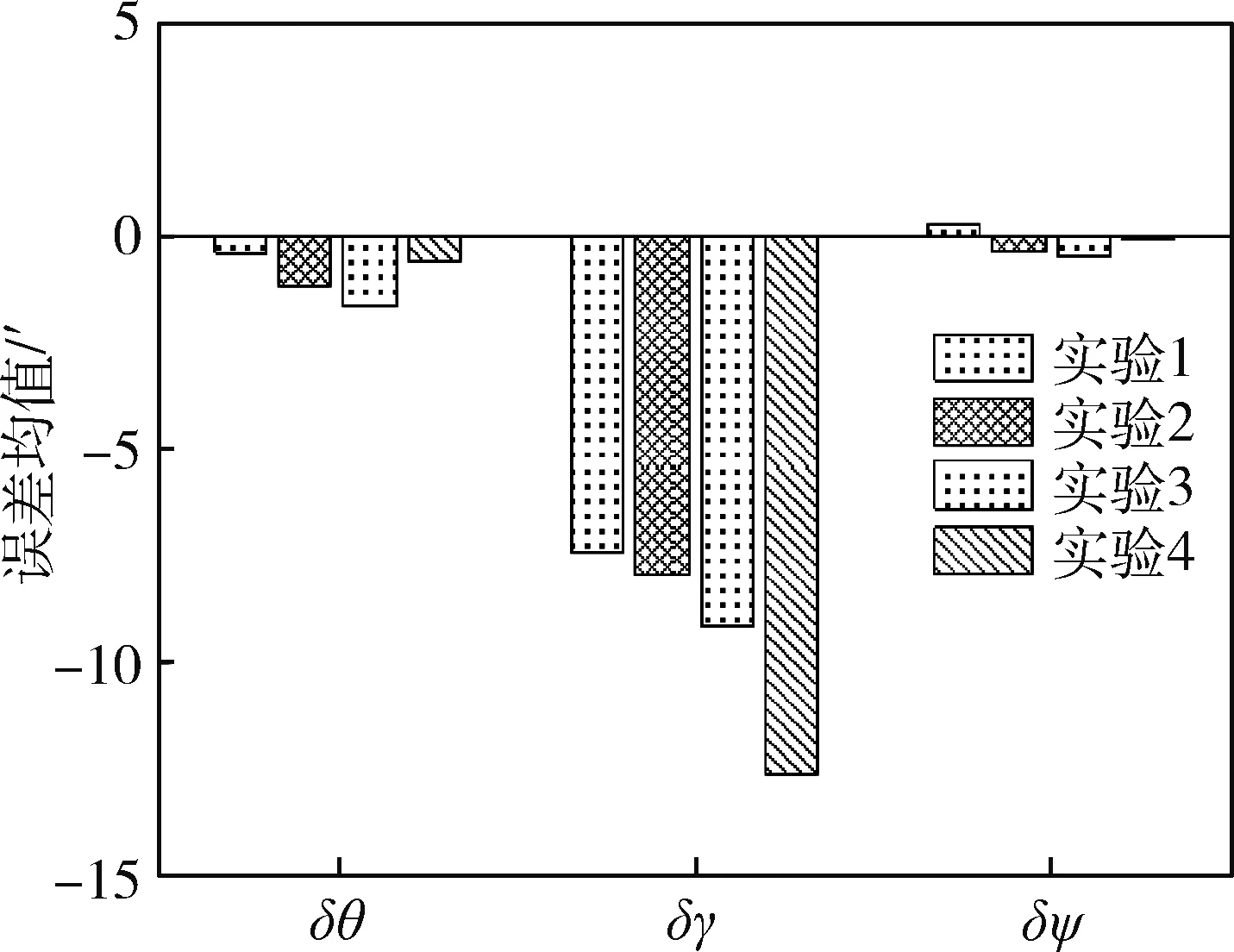
图5 精对准过程的误差均值
图6 精对准过程的误差标准差
5 结论
当载体处于静止状态时,采用GPS辅助微惯组进行初始对准,实验验证结果表明,保持姿态处于水平状态(小于5°)时,采用本文方法可以较高精度地完成微惯组的初始对准。
