数据驱动的陀螺随机游走故障诊断研究
2018-11-01吴新锋
吴新锋 段 然 许 琦 周 虎
北京航天自动控制研究所,北京 100854
近年来随着航天发射需求日益递增,惯性器件故障在运载火箭研制、测试过程中逐渐凸显,而随机游走故障在测试过程中通常难以发现,为航天发射埋下了重大安全隐患。激光陀螺以其高精度、高可靠性等优点,在航空、航天及航海领域得到了广泛应用。文献[1]针对惯组的参数故障(标度因子等突变)和线性、正弦缓变故障及输出故障(常零、满量程和倍频输出)提出了动态阈值故障检测方法,克服了传统恒定阈值不能反映载体运动变化的不足,但对于小幅值故障检测效果较差。文献[2]针对MEMS陀螺的小幅值故障提出了将假设检验与PCA算法相结合的故障检测方法,有效降低了噪声对小幅值故障检测的影响,对小幅值突变型故障有较好的检测效果,但难以检测随机游走故障。基于数据驱动的故障诊断,主要是从陀螺的输出时间序列中挖掘出故障特征并进行识别,而单纯的频谱分析无法满足故障诊断的需求,因而出现了一系列的时间序列分解方法,文献[3]和[4]分别将经验模态分解、集成经验模态分解运用到光纤陀螺的随机游走故障诊断中。随着深度学习热潮的再次来临,也出现了运用深度学习理论的故障诊断方法,其没有传统意义上的故障特征提取,特征提取与分类是同时完成的,直接利用大量样本数据对深度学习网络进行训练,如文献[5]将深度学习用于航空发动机零部件的故障诊断。
利用小波包理论、信息熵理论提取故障特征的方法及已有文献针对电力系统[6]、轴承[7]和陀螺[8]故障对该方法进行过研究,但基本都是针对突变型故障,而且针对陀螺研究时其输出模型运用常值项、周期项和白噪声项的和来描述,与陀螺实际输出有较大的差别,训练好的网络无法直接用于实测数据的诊断。针对输出模型与实际陀螺不一致的问题,本文创新性地将传统用来辨识陀螺噪声的Allan方差法用于模拟陀螺的随机游走故障,故障模型与实际陀螺相符,该方法也解决了工程中陀螺故障样本少的问题,训练好的网络可直接用于实测数据的诊断。另外,本文基于小波包、信息熵与神经网络的故障诊断研究,着重反映该方法在随机游走故障诊断方面的优越性,针对某型号激光陀螺静态测试场景下的脉冲数据进行仿真,验证了该方法的有效性。
1 故障数据模拟
为了使仿真的陀螺故障数据与陀螺的实际故障更相符,首先使用Allan方差分析实测无故障数据的随机误差特性,建立随机误差模型,在此基础上进行故障模拟。
1.1 Allan方差
1966年David Allan首次提出Allan方差来研究振荡器稳定性,由于陀螺等惯性器件本身也具有振荡器的特征,后来被IEEE 952标准引用来辨识和分析光学陀螺的噪声特性。
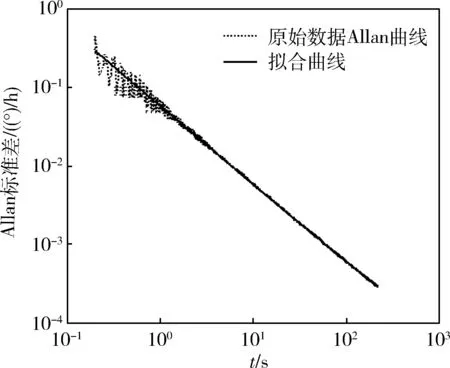
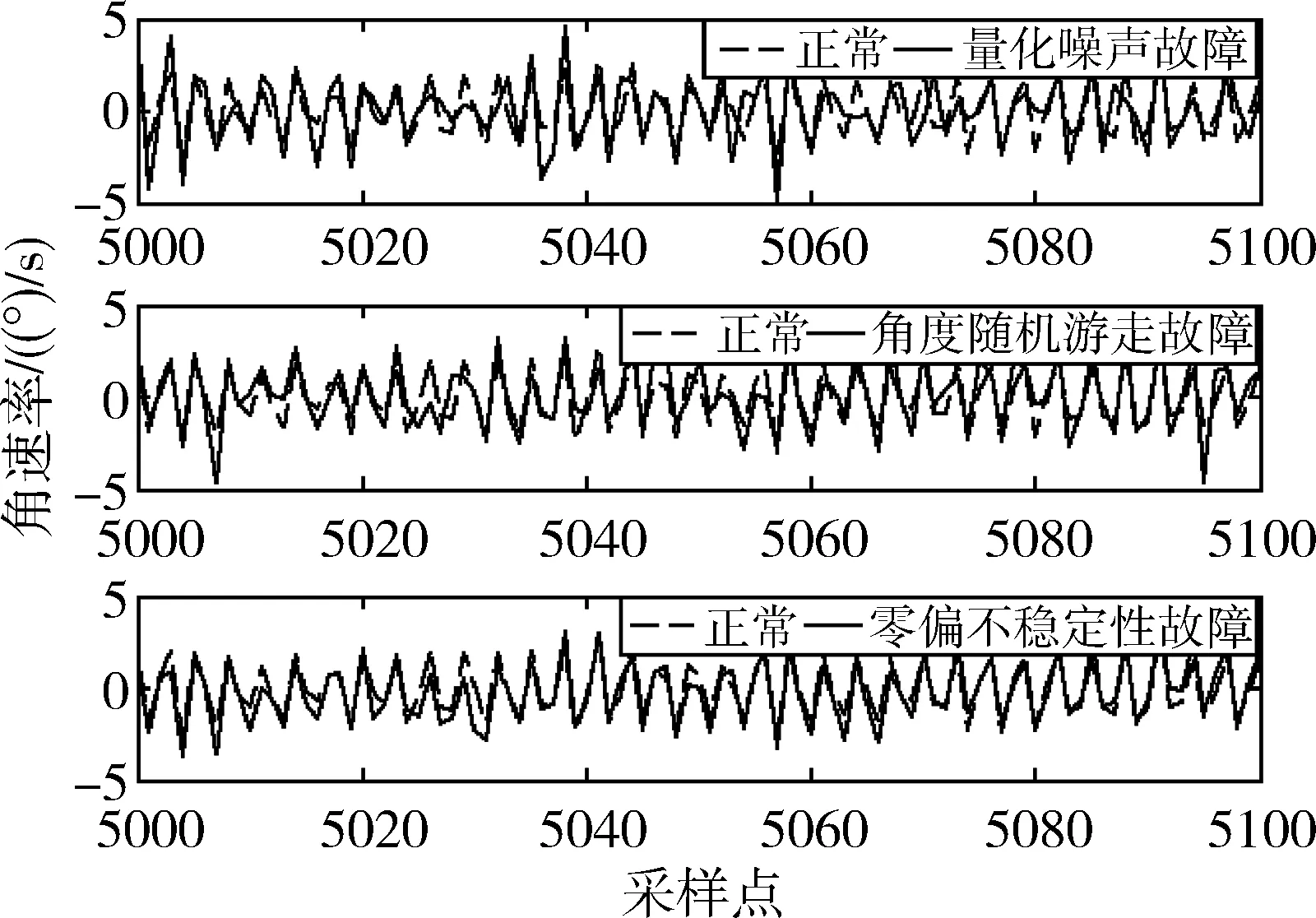
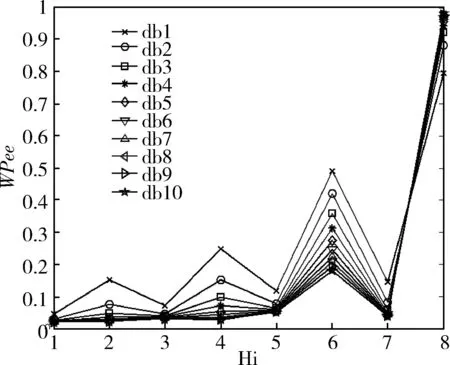
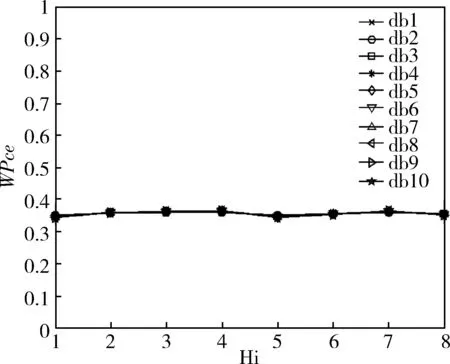
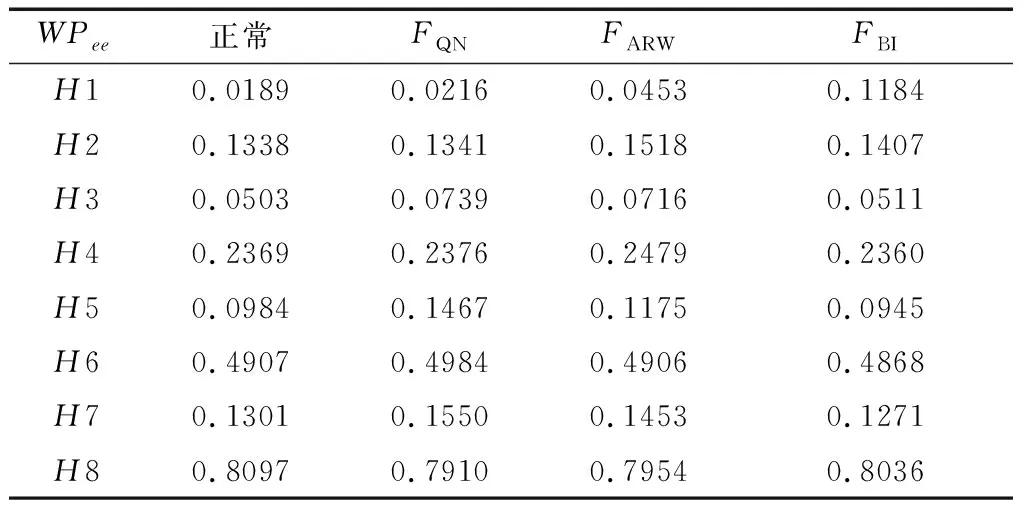
设有N个连续的采样点,采样周期为t0,将这N个点进行分组,每组包含n(n (1) 紧接着与该组独立的组的平均值为 (2) 其中,tk+1=tk+τ。则这N个采样点的Allan方差可以表示为 (3) IEEE 952标准中给出了光学陀螺通常包含的随机游走噪声有:量化噪声(Quantization Noise,QN)、角度随机游走(Angle Random Walk,ARW)、指数相关噪声(Exponentially Correlated Noise,ECN)、正弦噪声(Sinusoidal Noise,SN)、零偏不稳定性(Bias Instability,BI)、角速率随机游走(Rate Random Walk,RRW)及速率斜坡(Rate Ramp,RR),并且给出了各噪声的功率谱密度。其经典的Allan标准差-相关时间τ的双对数曲线如图1所示,曲线上不同的数值代表斜率,图中不同分段从左到右依次为上述的7种噪声。 图1 经典Allan标准差双对数曲线 由IEEE 952标准中各噪声的功率谱密度,根据下式Allan方差与功率谱密度的定量关系式[9],可以得到各类噪声的Allan方差。 (4) 假设各类型的随机误差统计独立,则总的Allan方差为各类型误差的Allan方差之和,即 (5) 由于指数相关噪声、正弦噪声相对其他5种噪声幅度较小,则 (6) 一般激光陀螺方差比较小,运用Allan标准差拟合能提高精度,即 (7) 将随机游走噪声分为白噪声和有色噪声,白噪声可以直接作为驱动噪声,不需要建模,只需对有色噪声进行建模,本文使用传递函数建模的方法。 对于线性系统,输出信号与输入信号存在如下的定量关系 Soutput(ω)=H(jω)Sinput(ω)H(jω)*T (8) 式中,Sinput,Soutput分别为输入、输出信号的功率谱密度;H(jω)为线性系统的传递函数矩阵。 如果采用功率谱密度为1的单位白噪声驱动有色噪声源,其传递函数就可以通过输出信号功率谱密度的平方根表示,上文已经给出各种噪声的功率谱密度,因此可求得各有色噪声源的传递函数。文献[10]在误差模型中将量化噪声看作是白噪声,而白噪声的Allan标准差曲线斜率为-1/2,这与Allan方差理论中量化噪声的Allan标准差曲线斜率为-1是矛盾的,本文将量化噪声当作有色噪声,因此误差模型中有色噪声包括量化噪声、零偏不稳定性、角速率随机游走与速率斜坡。 将各有色噪声的功率谱密度开平方,无理的传递函数运用马尔科夫过程近似,量化噪声的传递函数为纯微分环节,这里采用纯微分环节与小时间常数惯性环节的积来近似,得到随机误差模型如下 (9) 其中,u1,u2,u3,u4和u5为相互独立的单位白噪声;β=4Hz;ω0=0.05rad/s。 陀螺常见的随机噪声有式(9)中的5种,当随机游走噪声系数超过规定的范围时将其视为故障,因此随机游走故障可分为:量化噪声故障、角度随机游走故障、偏置不稳定性故障、角速率随机游走故障及速率斜坡故障,基于要求的噪声系数范围设定适当的噪声系数增量,将系数增量代入式(9)获得噪声增量,再叠加到实测无故障数据作为相应的故障数据。 传统的基于傅里叶变换的频谱分析只能对信号进行全局的描述,对具有非平稳特征的陀螺信号,需要同时进行频域和时域的描述,小波包变换可以同时描述信号时、频域的局部特征,广泛应用在非平稳信号的分析中。本文首先对待测信号进行小波包分解与重构,再提取各小波包的熵特征,作为故障特征量。 陀螺输出的角速率信号un(k)通过式(10)进行小波包分解, (10) 第j层第m个小波包的重构信号为 (11) 熵的概念最早出现在热力学中,用来描述体系的混乱程度,后来被引用到信息论中,来描述信号的复杂度,当设备出现故障时,其输出信号的能量组成往往会发生变化。小波包能量熵(Wavelet Packet Energy Entropy,WPEE)是结合小波包理论与信息熵理论对信号能量组成复杂度的描述,小波包特征熵(Wavelet Packet Characteristic Entropy, WPCE)是另一种对信号能量组成的描述,二者定义如下: 小波包能量熵定义为:对信号进行j层小波包分解后,可以得到小波包分解序列S(j,k),k=0,1,…,2j-1,小波包可以看作是对信号的一种划分,则对应的组分分布概率可以表示为 ε(j,k)(i)=Ei/E,(i=1,2,…,N) (12) (13) 式(13)中,Hj,k表示小波包分解树中第j层第k个小波包的小波包能量熵。 小波包特征熵与能量熵不同之处在于组分分布概率,定义为 (14) 其中,SF(j,k)(i)是S(j,k)的离散傅里叶变换序列的第i个值。 利用神经网络对非线性映射关系的拟合能力和良好的泛化能力进行故障模式的辨识。选择BP网络作为分类器,其基本原理是梯度最速下降法,其训练过程包括信息正向传递与误差的反向传播2个过程,通过不断调节网络权值和阈值使实际输出与期望输出的误差平方和最小。为了抑制学习过程的振荡,避免可能发生的学习发散,引入动量项来改善收敛性。 BP网络的输入节点个数为故障特征向量的维数,输出节点个数为故障模式的类数,采用单隐含层,隐含层节点数个数通过式(15)的经验公式确定 (15) 其中,j,k分别是输入层、输出层节点数;α为修正系数,取1~10之间的整数。 常温下,采集某型号激光陀螺的静态测试数据2000s,采样周期0.02s,获得100000个采样数据。故障诊断的总体思路如图2所示。 图2 陀螺故障诊断流程图 激光陀螺的随机游走误差中包含有很多误差源,但一般只有3~4种主要分量,国内外的文献中一般取量化噪声、角度随机游走与零偏不稳定性。激光陀螺的原始测试数据如图3所示,利用式(3)计算Allan方差,使用上述3种噪声源也即式(7)的前3项进行拟合得到图4所示的Allan标准差双对数曲线,从图4中也能发现已有的这段曲线主要以这3种为主,如果要辨识剩余的几种需要增大相关时间,在考虑误差不变的情况下,需要更多采样数据,这里采用上述3种误差源来拟合,拟合得到上述3项误差源的系数如表1所示,将各参数代入式(9),即得到该型激光陀螺的随机误差模型。 图3 原始数据 图4 Allan标准差双对数曲线 表1 误差系数拟合结果 运用建立的误差模型仿真生成数据,分析数据的Allan方差得到仿真数据的Allan标准差曲线,与图4中的原始数据拟合曲线比较如图5所示,可以看到两曲线基本重合,证明本文建立的随机误差模型是有效的。 图5 仿真数据Allan标准差双对数曲线 根据上文的分析,将随机游走故障模式设定为3类:量化噪声故障、角度随机游走故障及零偏不稳定性故障,使用1.3节的方案进行故障模拟,各故障信号与正常信号对比取其中一段如图6所示。仿真生成量化噪声故障数据、角速率随机游走故障数据、零偏不稳定性故障数据及无故障数据样本各200个,其中一半作为训练样本,另一半作为测试样本。 图6 各故障信号与正常信号对比 在提取小波包熵特征之前,首先需要确定小波包分解的基函数。一般为了避免小波包之间的混叠,采用正交小波基,常用的有Haar、Daubechies、Coiflets、Symlets及Meyer基函数,另外小波基函数的紧支性、正则性及消失矩等特性都会影响小波包分解的效果,目前还没有小波基函数选择的通用理论,但故障诊断领域一般选择Daubechies小波,简称为“dbN”小波,N表示消失矩。以无故障数据为例,分别采用db1~db10小波进行3层小波包分解并提取能量熵特征如图7所示,可以看到dbN小波的消失矩N对能量熵特征有较大影响;小波包特征熵特征如图8所示,各个小波包的特征熵基本相当,无法显著表征小波包的特征,而且几乎不随小波基函数变化,为了更好地表现不同小波包之间的差异性,本文特征提取方法选择小波包能量熵,小波基函数选择db1小波,也就是Haar小波。 图7 dbN小波下的小波包能量熵 图8 dbN小波下的小波包特征熵 选择Haar小波分别对4种模式(无故障及3种故障)下的样本进行小波包分解与重构,利用2.2节的公式提取各小波包的能量熵如表2所示。 表2 各模式样本的小波包能量熵 分类器采用BP网络,输入层8个节点,输出层4个节点,激励函数为线性函数,隐含层取12个节点,激励函数为Sigmoid函数,提取正常模式及3种故障模式下共400个训练样本的小波包能量熵特征,对BP网络进行训练,取学习率0.0001,为抑制振荡引入动量项,动量因子0.7,训练误差曲线如图9所示,可以看到网络训练误差最终趋于稳定。 图9 训练误差随训练次数变化曲线 利用另外的400个样本对该故障诊断方法进行测试验证,对网络输出向量各元素取“四舍五入”,各模式诊断正确率均达到100%,因为测试样本故障引入时叠加的噪声的系数偏差与训练样本在同一范围,当故障相对训练样本适当减轻,即减小模拟故障时的系数偏差时,以常见的角度随机游走故障和零偏不稳定性故障为例,仿真得到2种模式故障诊断正确率如表3所示,诊断正确率有所降低,说明随机游走达到一定量级时才能检测到,因此在生成训练样本时需要通过噪声系数偏差设定故障的程度,故障越轻微检测灵敏度越高,但若过于轻微会导致与无故障样本的故障特征量差异过小,导致分类器训练时很难收敛,工程应用中通常会让随机游走不超过相应的任务指标,因此可以参考该指标引入故障。 表3 故障相对训练样本减轻时的诊断结果 针对陀螺随机游走故障提出了一种基于小波包、信息熵与神经网络理论相结合的数据驱动的故障诊断方法。根据激光陀螺静态测试无故障数据进行Allan方差分析获得其各项随机噪声的系数,并建立随机误差模型,进而仿真生成无故障及各类故障数据作为训练样本和测试样本。然后,对训练样本进行小波包分析,提取小波包能量熵作为故障特征向量,用于对BP网络分类器进行训练,网络趋于稳定后,用测试样本对该方法进行测试。测试结果表明,该方法故障检测灵敏度较高,对于陀螺随机游走故障具有比较好的诊断效果。本文研究的陀螺静态测试数据故障诊断方法经过适应性改进即在线测试信号剔除趋势项后,也可适用于在线故障诊断,扩展性好。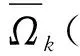

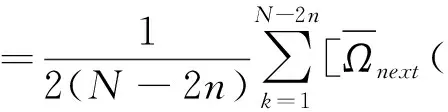



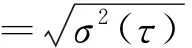
1.2 随机误差建模

1.3 故障模拟
2 故障特征提取
2.1 小波包分解与重构
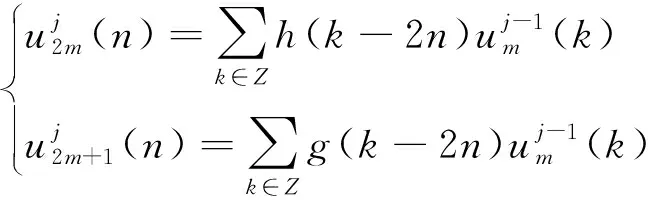
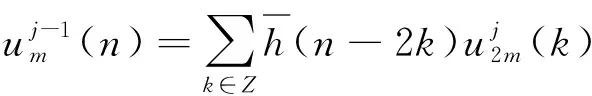
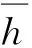
2.2 熵特征提取
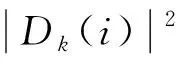
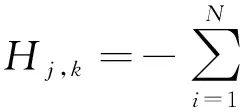

3 故障模式分类
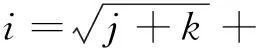
4 仿真试验

4.1 激光陀螺误差模型



4.2 故障特征提取
4.3 分类器训练与测试



5 结论
