Huber-based滤波在非合作航天器相对导航中的应用

施常勇 王 向

1. 上海航天控制技术研究所，上海 201109 2. 上海市空间智能控制技术重点实验室，上海 201109

非合作航天器相对导航是完成在轨服务的前提，主要航天大国均开展了相关研究。在对非合作航天器的测量过程中，测量设备的误差通常较大，角闪烁、目标机动等一些不确定因素也会对测量产生影响，为提高相对控制的精度，一般引入滤波处理。

目前，扩展卡尔曼滤波(EKF)是研究相对导航问题的主要手段，文献[1]和[2]均采用EKF作为导航滤波器，且在文中假设噪声输入为严格的高斯过程，然而实际问题常常不满足这一条件，严重时会导致滤波发散。对于存在非高斯噪声输入的系统，通常采用的滤波方法有UKF滤波[3]、H∞滤波[4]、L2/L∞滤波和L1滤波[5]等。1964年Huber 提出了广义极大似然估计，即M估计，并提出一种用于解决在Gaussian分布附近存在一定对称干扰的随机量(即混合高斯分布)问题的实用方法，即Huber方法[6]。该方法结合l1/l2两种范数构建代价函数，对于干扰为高斯分布的情形，可以使最大渐进估计方差达到最小；其鲁棒性优于基于l2范数的估计方法，尽量保持了纯高斯分布时l2范数的估计效率，同时结合Kalman滤波的优点，形成了Huber-based滤波(HBF)，该滤波器通过结合l1和l2范数估计器的特点，在处理对于量测噪声为受污染的高斯白噪声时具有较强的鲁棒性，能够很好地实现系统的状态估计。

本文将HBF应用于非合作航天器相对导航中。仿真研究针对输出噪声为高斯和混合高斯分布的情况，考虑目标存在机动过程，对比了HBF滤波与EKF滤波的性能。具体安排如下：第1节，简要介绍HBF算法；第2节，给出相对导航系统模型；第3节，针对不同工况进行数学仿真校验；第4节，对全文进行总结。

1 Huber-based滤波器

设系统方程为：

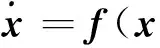
(1)

其中，x和z分别为状态值和量测量;ω和ν分别为系统模型误差和测量噪声。

1.1 状态预测

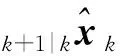
(2)

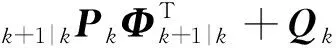
(3)

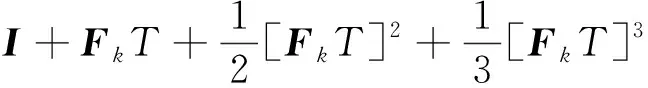
(4)

Fk=∂f(x,u,ω)/∂x|x=xk

(5)

其中,Φk/k-1为离散系统一步转移矩阵;T为滤波周期;xk+1|k和Pk+1|k为预测状态估计值和状态估计误差协方差阵。

1.2 测量更新

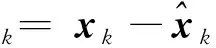
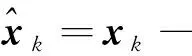
(6)

系统测量矩阵离散化后可写成如下形式：

(7)

定义如下变量：

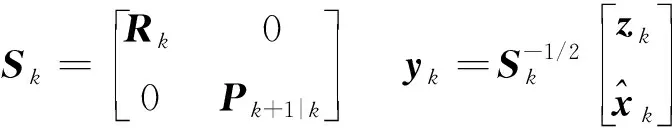
则：

yk=Mkxk+ξk

(8)

求解式(8)可采用线性回归近似的Huber方法，定义代价函数ρ(·)，取其最小值， Huber代价函数定义如下：

(9)

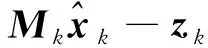
(10)

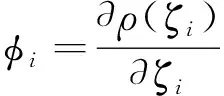
(11)

求解上式可通过迭代解法：

(12)

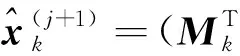
(13)

Huber定义了一种代价函数的形式：

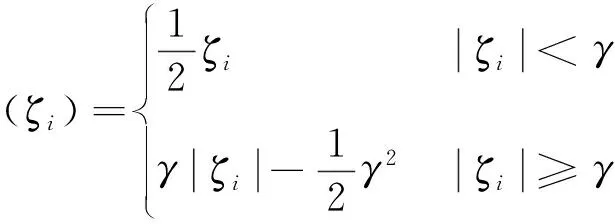
(14)

γ为调节参数，这种代价函数结合了l1，l2范数的性质，具有较好的鲁棒性，其中γ在1～2 之间取值，一般选择调节因子为1.345[7-8]，Huber已证明，当ρ(·)函数选择式( 14) 的形式，选取该调节因子，HBF对受污染的高斯分布具有渐近最优鲁棒性。

状态估计误差协方差阵为

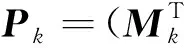
(15)

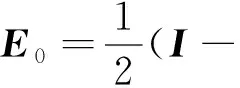
Xk+1=Xk+Ek

(16)

(17)

式中，Λ为待求矩阵。

2 相对导航系统设计

相对导航中，两航天器的关系如图1所示。

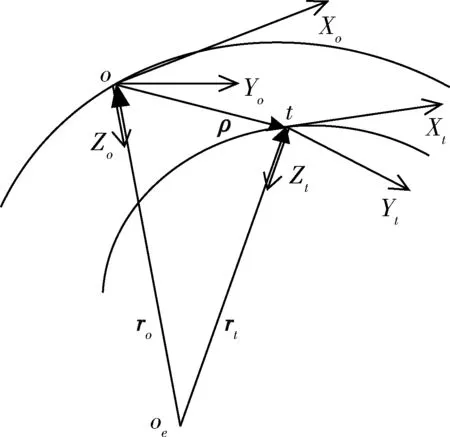
图1 相对导航坐标系

设跟踪航天器相对J2000惯性系的位置矢量为ro；目标航天器相对J2000惯性系的位置矢量为rt；目标航天器相对跟踪航天器的位置矢量为ρ。

1)相对运动方程[12]

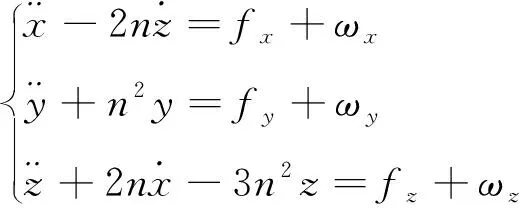
(18)

其中，n为跟踪航天器轨道角速度；fx，fy和fz为轨道调整或变轨过程中控制力引起的加速度，可以通过加速度计测量得到；ωx，ωy和ωz为干扰加速度，主要由方程推导过程中的近似处理以及各种摄动加速度引起，用白噪声近似。将式(18)写成矩阵形式为：

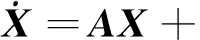
(19)

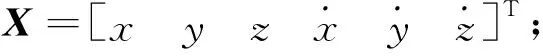
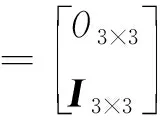
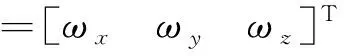
2)相对测量设备测量量定义

相对导航常用的测量设备有微波雷达和激光雷达、光学相机与激光组合测量系统等，输出形式如图2所示。

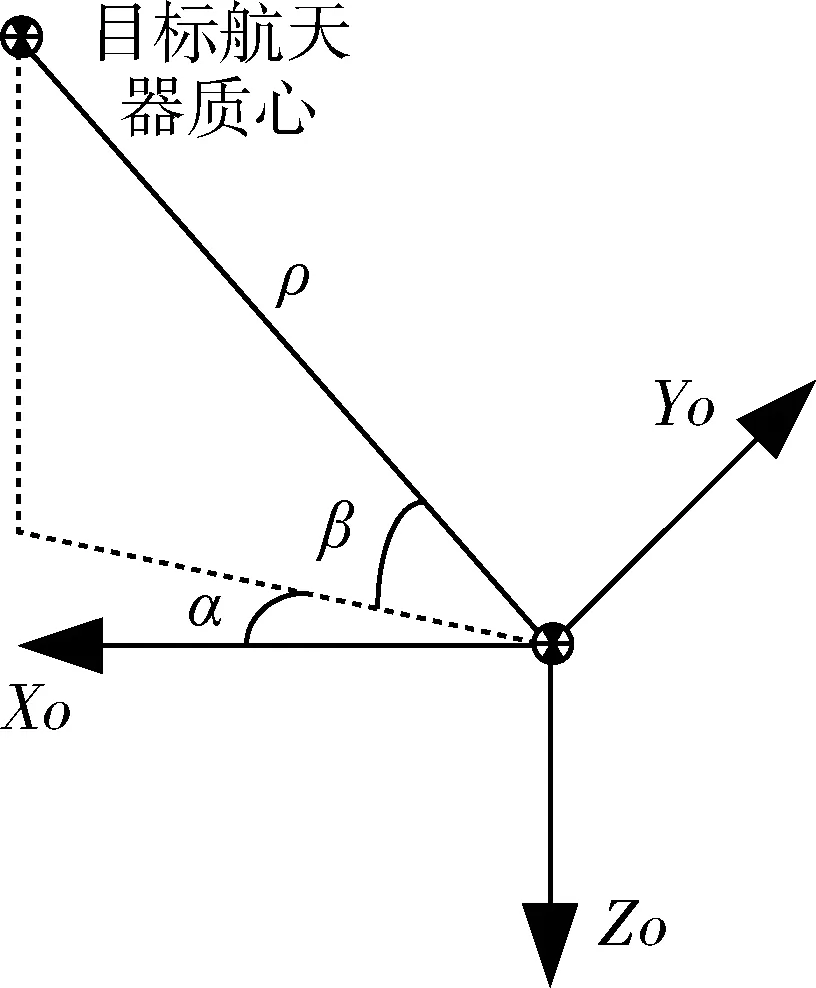
图2 相对测量设备输出定义

ρ为目标星相对于追踪星的视线距离；

临床教学重视理论、实践相结合，教学目的是培养学生独立思考和解决问题的能力，学习疾病基础知识。因妇产科学实践性和理论性较强，妇产科患者疾病涉及隐私部位，患者自我保护意识较强，普遍存在让抗拒带教学生进行检查现象，加大治疗难度[7]。传统教学模式学生学习主动性下降，重复学习情况严重，学生探究性不强；老师教授什么知识就学什么，学习较为随意，没有意识到妇产科学学习的重要性；传统教学模式也是以老师为主的“填鸭式”教学，老师为主导，学生被动学习，独立学习意识和思考意识缺乏。该种教学方式培养出的医师已经不能适应多变的临床情况和复杂的医疗环境，可能出现诊断失误或其他医疗事故，严重威胁患者安全[8]。

α为目标星在追踪星相对导航敏感器测量坐标系中的方位角，定义为目标星相对追踪星视线在测量系XY平面的投影与X轴之间的夹角，偏向+Y轴方向为正；

β为目标星在追踪星相对导航敏感器测量坐标系中的高低角，定义为目标星相对追踪星视线与其在测量系XY平面投影之间的夹角，偏向-Z轴方向为正。

具体定义为：

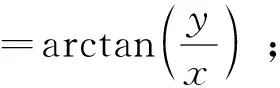
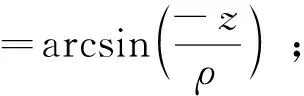
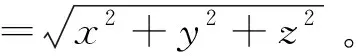
3)量测与量测方程

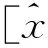
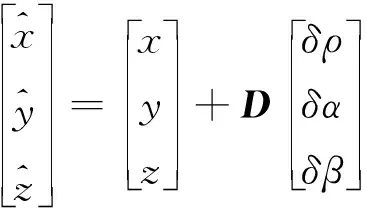
(20)

其中：

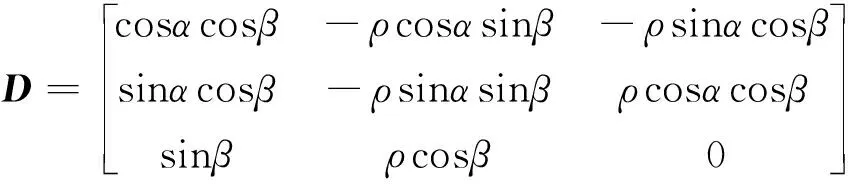
相对导航量测方程为：

Z=HX+DV

(21)

间接测量的量测噪声方差矩阵为：

E(DV, (DV)T)=D·E(V,VT)·DT=DRDT

(22)

3 仿真校验

为校验HBF在相对导航系统的可用性和适应性，采用高精度轨道动力学仿真2颗航天器的空间飞行轨迹，敏感器的误差设置如表1，对高斯分布型噪声、混合高斯噪声及目标机动等3种工况，分别采用HBF和EKF进行仿真校验。

相对导航周期：T=0.4s。

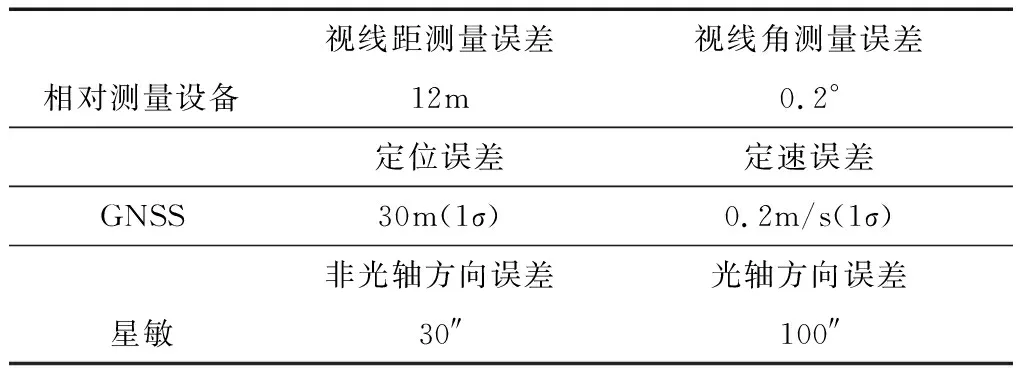
表1 敏感器误差参数设置值(3σ)

3.1 正常误差工况

采用表1中设置的敏感器误差参数，HBF和EKF仿真曲线如图3～4所示，从图中可以看出，HBF相对EKF处理误差小，且较平滑，其中HBF导航精度为2.03m，速度精度0.04m/s，而EKF相对导航位置精度为3.59m，相对速度精度为0.11m/s。

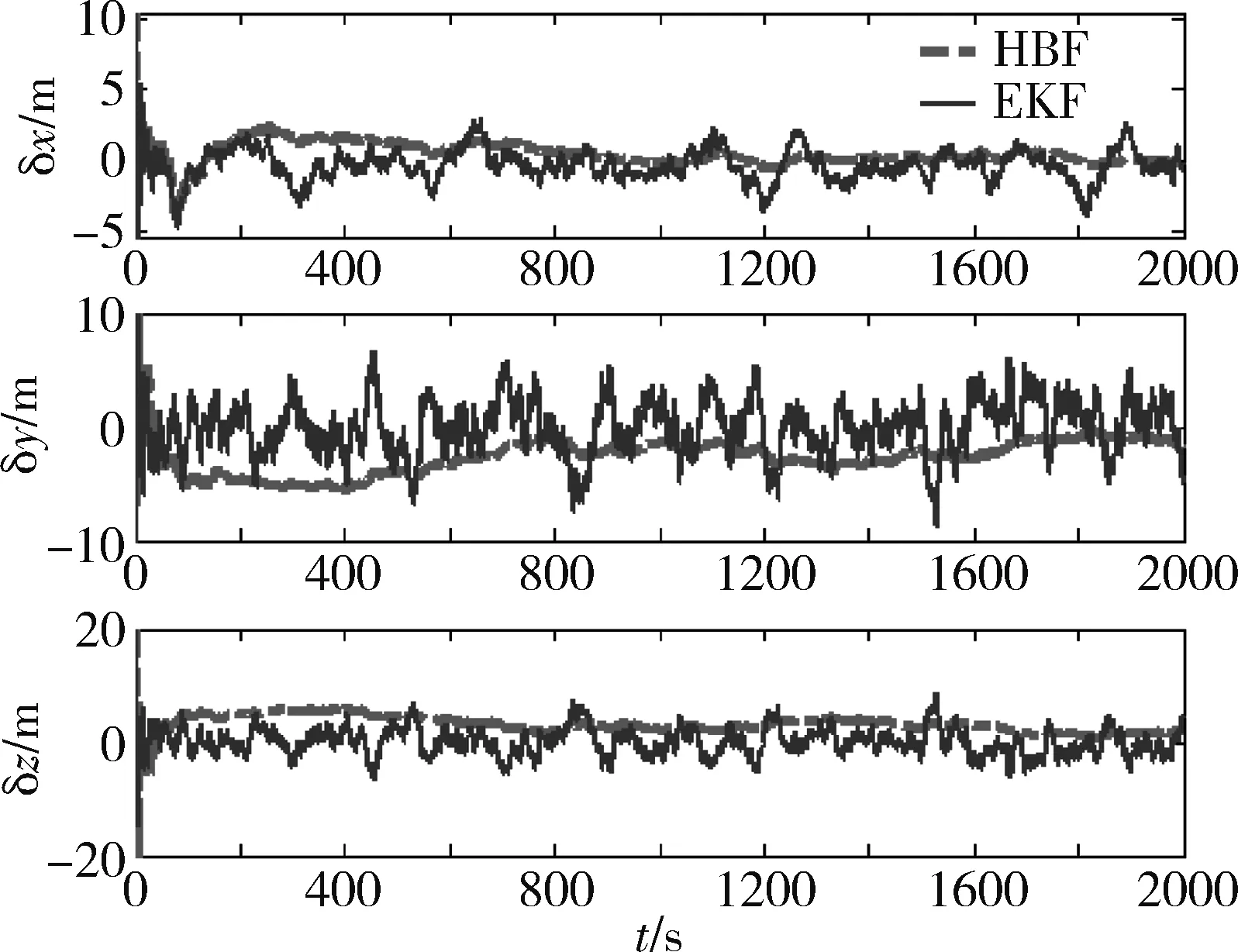
图3 三轴相对位置估计误差

图4 三轴相对速度估计误差

3.2 混合高斯噪声模型工况

为检验HBF和EKF在混合高斯模型下的仿真性能，相对测量设备的误差采用混合高斯噪声模型，其表达式[15]为：

f(υk)=(1-ε)N(0,σ1)+εN(0,σ2)

(23)

仿真时，ε取0.6，σ2=2σ1，由表2可见，无论是高斯还是混合高斯分布情况下，HBF均表现出较好的导航性能：

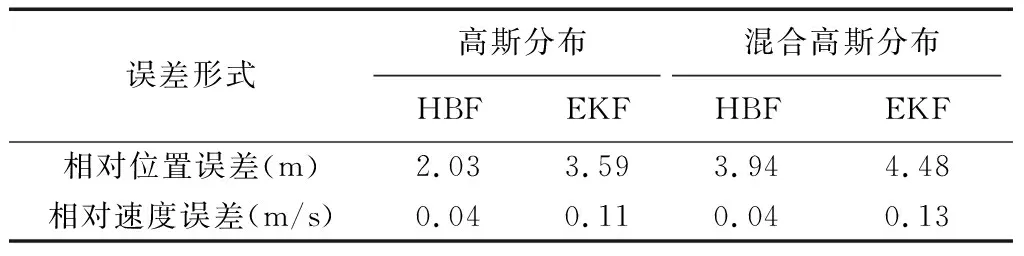
表2 各算法运行结果

3.3 目标机动工况

采用表1参数，在t=500s时，目标星以0.1m/s的速度远离跟踪星(x向)，则两型滤波器的滤波误差曲线如图5～6所示：

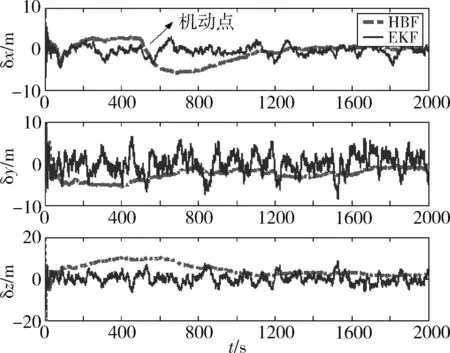
图5 三轴相对位置估计误差(目标机动)

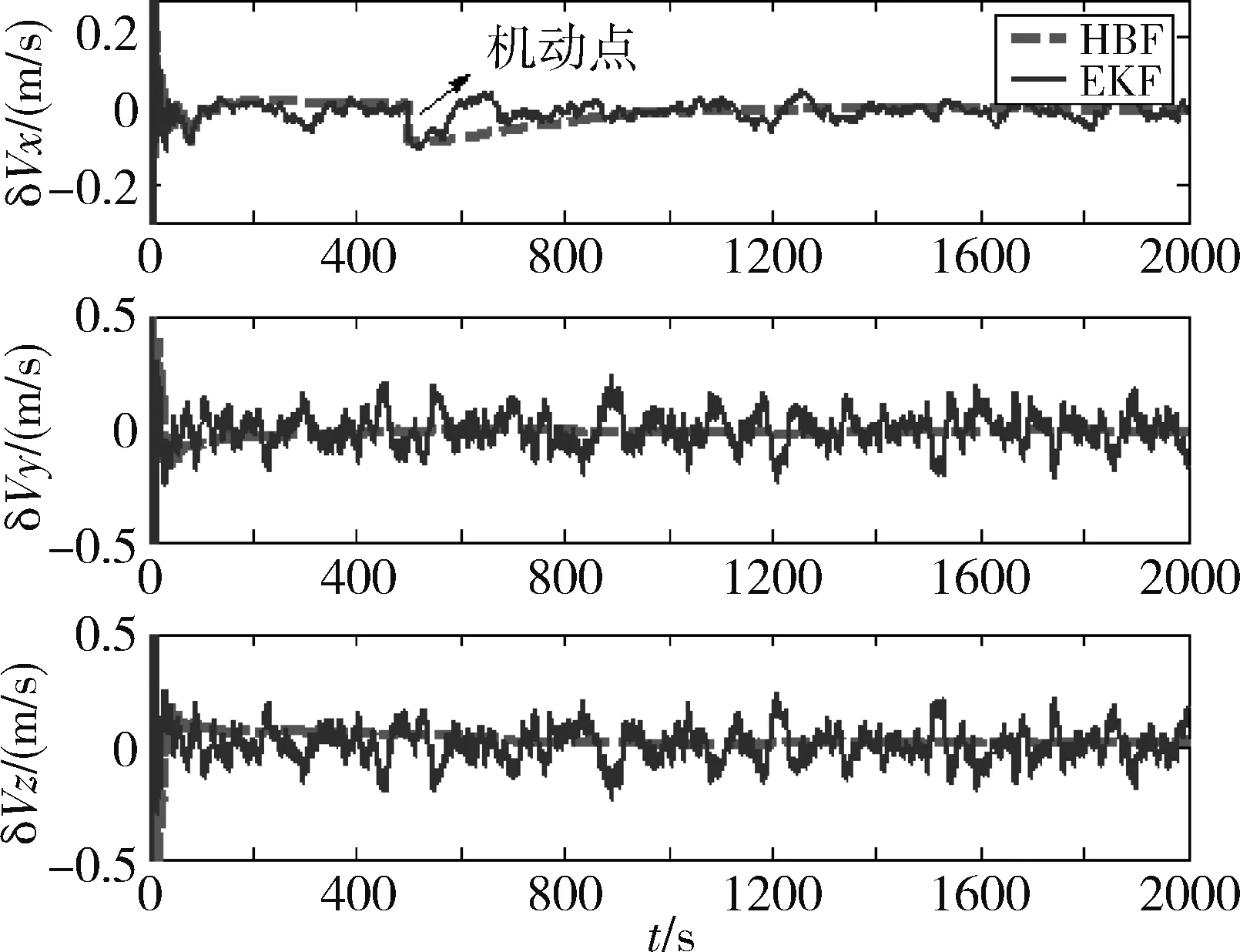
图6 三轴相对速度估计误差(目标机动)

从图中可以看出，EKF比较快速地敏感到速度的增加，而HBF则有一定的延迟，但HBF相对较平滑地实现了位置和速度的滤波估计，且最终精度依旧比EKF高。

4 结论

针对传统Kaman滤波在输入噪声为非高斯噪声时导航精度下降、甚至发散的问题，研究了Huber-based滤波器在空间非合作航天器相对导航系统中的应用技术，采用间接滤波方法，搭建仿真模型，对所设计的相对导航系统进行了仿真校验，并将其与EKF进行对比分析。仿真表明，HBF性能较EKF优，且具有较好的鲁棒性和稳定性，具有较强的工程应用价值。