一种不平整地形下足式机器人的主动柔顺控制方法*
2018-11-01张世俊
张世俊 邢 琰,2 胡 勇,2
1.北京控制工程研究所,北京 100190 2. 空间智能控制技术重点实验室,北京 100190
与常见的轮式移动机器人相比,足式机器人具有更好的地形适应能力,针对不平整地形下的足式机器人步态规划与控制,已有许多研究成果[1-3],主要思路为根据周围的地形信息,选择合适的落足点,进而规划运动轨迹。然而该方法存在以下限制,落足点的选取依赖于机器人对周围地形感知的准确度,并且由于计算量较大,需要在步态中加入静止站立阶段用于机器人运动规划。然而对于崎岖程度相对不大的地形,步态规划算法并不需要在每一步根据地形信息选取摆动腿的落足点,可以通过主动柔顺控制方案使得机器人在不需要地形信息的情况下,对外部环境表现出柔顺特性,从而提高机器人对不平整地形的适应能力,使得机器人能够快速通过不平整的地形。
迄今,针对足式机器人的主动柔顺控制研究已取得了许多成果,阻抗控制[4-8]是一种常见的主动柔顺控制方法,它基于机器人足端与地面环境的接触力模型,通过反馈调整足端位置达到控制接触力的目的,该方法相当于将接触力误差通过一个二阶滤波器得到足端位置调整量,与参考足端轨迹相加后通过逆运动学模型生成关节角指令,这种基于足端工作空间的修正方法并没有给出关节角速度的修正方法,一定程度上影响关节PD控制的关节角度跟踪效果;Zucker和Winkler等[9-10]利用逆动力学控制和力反馈控制,结合低增益系数的关节PD控制,实现了机器人关节空间内的主动柔顺性,并成功将其应用于“Little dog”机器人,该方法通过逆动力学模型预测接触力,力反馈控制直接将接触力误差转换成关节力矩施加到关节上,这需要精确的动力学模型和地形信息,同时需要机器人关节能够实现高精度力矩控制。
针对上述分析,针对未知不平整地形提出一种主动柔顺控制方法,包括基于关节空间的阻抗控制、姿态柔顺控制和关节PD控制,其中基于关节空间的阻抗控制方法将力反馈信号转换到关节空间,通过阻抗滤波器同时生成关节角度修正量和关节角速度修正量,再将修正后的关节角度和角速度指令输出给关节PD控制器;姿态柔顺控制通过机身姿态角误差计算支撑腿长度调整量,进而通过阻抗滤波器得到腿长修正指令,综合设计关节柔顺控制和姿态柔顺控制的滤波器参数,使机器人腿部关节和机身姿态对不平整地形表现出柔顺特性,通过不平整地形时更加平稳。最后本文的主动柔顺控制方案在四足机器人中得到了仿真验证,实现了机器人在未知不平整地形下的稳定行走。
1 整体步态规划与控制框架
以四足机器人为例设计主动柔顺控制方案,机器人构型如图1所示,机器人包含4条腿,每条腿具有3个关节,分别为根关节(偏航自由度)、髋关节(俯仰自由度)和膝关节(俯仰自由度)。定义固连于机器人身体的机体坐标系{B},原点位于机器人身体中心,x轴指向机器人右方,y轴指向机器人正前方,z轴垂直于身体向上。
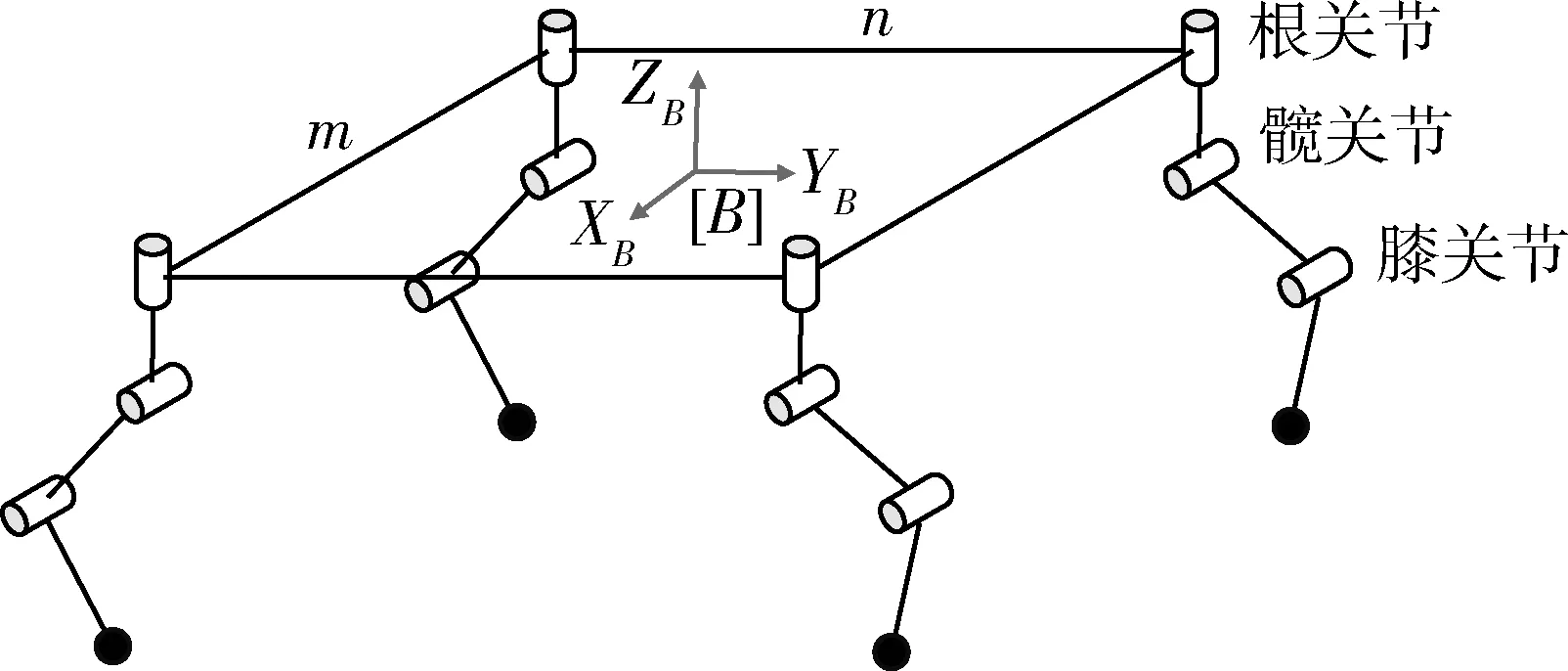
图1 四足机器人结构示意图


图2 整体步态规划与控制框架
主步态规划模块包括重心运动轨迹规划、摆动腿轨迹规划和腿部逆运动学模块。四足机器人的典型步态有慢走步态(walk)、对角步态(trot)、溜蹄步态(pace)和疾跑步态(gallop)等,与其他几种步态相比,对角步态具有较高的能效比和较大的速度适应范围,对称性较好,易于保持机器人运动的稳定性,是一种具有较高实用性的动态步行方式[11]。因此,本文采用对角步态作为四足机器人在不平整地形下行走的主步态。机器人摆动腿轨迹采用如下具有复合摆线形式的轨迹[12]:
(1)
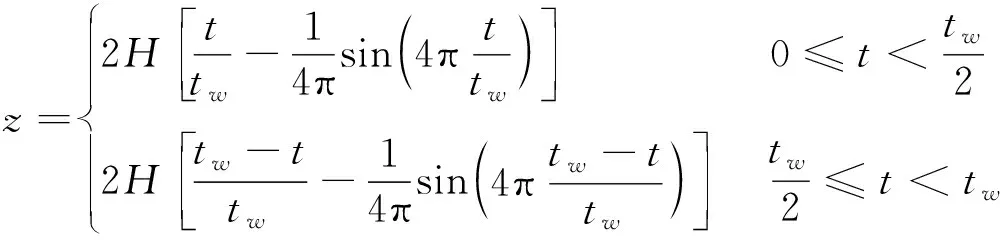
(2)
其中,s为跨距;H为抬腿高度;tw为摆动相持续时间。该足端轨迹满足位置、速度和加速度连续无突变,摆动相与支撑相切换平滑。腿部逆运动学模块将足端轨迹转换到关节空间内的关节角轨迹,将其作为控制系统的参考指令,从而驱动各个关节实现四足机器人的前进步态。
2 主动柔顺控制
2.1 基于关节空间的阻抗控制
基于关节空间的阻抗控制框图如图3所示,由位置控制内环和力控制外环组成,主要思想为由外环控制器将足端的接触力误差映射到关节空间内,再通过阻抗滤波器和积分器生成关节角和关节角速度修正指令,用于修正步态规划器给出的关节角和角速度参考值,然后将生成的关节角和角速度指令输出给内环位置控制器,通过反馈调整足端位置达到控制接触力的目的。采用基于关节空间的阻抗控制使得机器人腿部关节直接响应不平整地形造成的接触力突变,从而实现机器人的主动柔顺性。
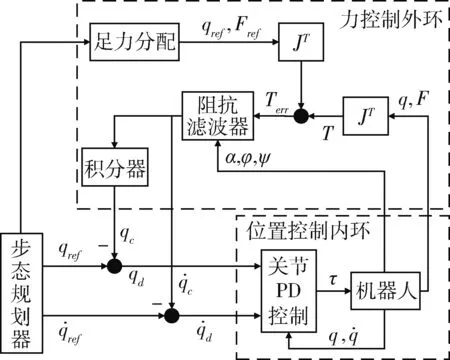
图3 基于关节空间的阻抗控制框图
根据步态规划中给出的参考轨迹,每条腿关节空间内的力矩误差可按下式计算[13-14]:
Terr=JT(qref)Fref-JT(q)F
(3)

(4)
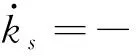
(5)

2.2 姿态柔顺控制
机器人在通过不平整地形时,四条腿的落足点高度不一致,会导致机身姿态发生偏转,从而影响机器人步态的稳定性,因此需要加入机身姿态反馈控制保证机器人身体姿态保持稳定。机身姿态反馈控制利用支撑腿长度的调整使机身实际姿态与期望姿态重合,通过调整左右腿长度差改变机身滚转角,通过调整前后腿长度差改变机身俯仰角。

图4 姿态调整图
定义机身水平坐标系{L},原点与机体坐标系{B}相同,x轴水平向右,y轴水平向前,z轴垂直向上。设机体坐标系{B}相对于机身水平坐标系{L}的欧拉角按照1-2-3转序定义:俯仰角α,滚转角φ和偏航角ψ,则姿态转换矩阵可表示为:
其中,s1=sin(α);c1=cos(α);s2=sin(φ);c2=cos(φ);s3=sin(ψ);c3=cos(ψ)。则根据测得的关节角度和身体姿态,有
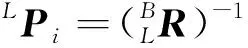
(6)
其中,BPi为支撑腿i的足端在坐标系{B}中的坐标;LPi=[pixpiypiz]T为支撑腿i的足端在坐标系{L}中的坐标,则可以估计出调整俯仰角和滚转角所需的腿长修正量:
(7)
(8)
其中,plx为左支撑腿足端x轴坐标;prx为右支撑腿足端x轴坐标;pfy为前支撑腿足端z轴坐标;pbz为后支撑腿足端z轴坐标;zep和zer分别为对应调整俯仰角和滚转角的腿长修正量;φ0和α0为滚转角和俯仰角阈值,可根据平地行走身体波动状况设定,当姿态角超过一定阈值时,姿态控制器开始发挥作用。将上述计算得到的支撑腿长度调节量通过一阶阻抗滤波器后生成支撑腿长度修正指令,滤波器传递函数如下:
(9)
其中,(kp,bp)和(kr,br)分别为对应俯仰角和滚转角的阻抗滤波器参数。
令通过滤波器后的俯仰角和滚转角的支撑腿长度修正指令分别为zcp和zcr,再将该腿长度调节量按式(10)分别分配至四条腿:

(10)

设计姿态阻抗滤波器的原因主要有以下2点,1)使机器人机身姿态调整对不平整地形表现出柔顺特性,延缓姿态反馈的响应速度,使姿态调整与足端接触力反馈相比表现为慢周期特性;2)机器人阻抗控制存在正反馈的现象,例如当机器人姿态向后倾斜时,后支撑腿的支撑力大于期望支撑力,此时根据关节阻抗控制需要收缩后支撑腿以期减小接触力,从而加剧机器人姿态的偏转,因此通过引入姿态阻抗滤波器,综合设计关节柔顺控制和姿态柔顺控制的滤波器参数使机器人在通过不平整地形时保持平稳。
3 四足机器人仿真
在ADAMS中搭建四足机器人虚拟样机模型,采用ADAMS和SIMULINK联合仿真技术进行虚拟样机仿真[15]。机器人总质量200kg,大腿长度为0.4m,小腿长度为0.3m。
为验证本文提出的控制方法的有效性和机器人通过不平整地形的能力,本文进行如下两种地形仿真:
不平整地形1:机器人通过一段左右错落的不平整地面,地形高度落差最大值为6cm;
不平整地形2:机器人通过上下坡的地形,地形高度落差为16cm,坡度为10°。
针对每种地形情况分别做2组仿真进行对比,2组仿真中步态规划算法相同,其中一组采用本文提出的柔顺控制和姿态控制方法,另一组只采用关节PD控制。整个仿真过程中,机器人没有任何地形信息,仅依靠自身的关节角、角速度和姿态角测量信息,实现在不平整地形下的稳定行走。
3.1 不平整地形1仿真
仿真中机器人通过一段左右错落的不平整地面,采用主动柔顺控制时仿真截图如图5所示,仿真中机器人在2~8s期间通过不平整地形,机器人前进距离和速度曲线如图6所示,可知2种方法均能使机器人通过不平整地形,采用柔顺控制时机器人前进速度波动更小,对地形适应能力更强。
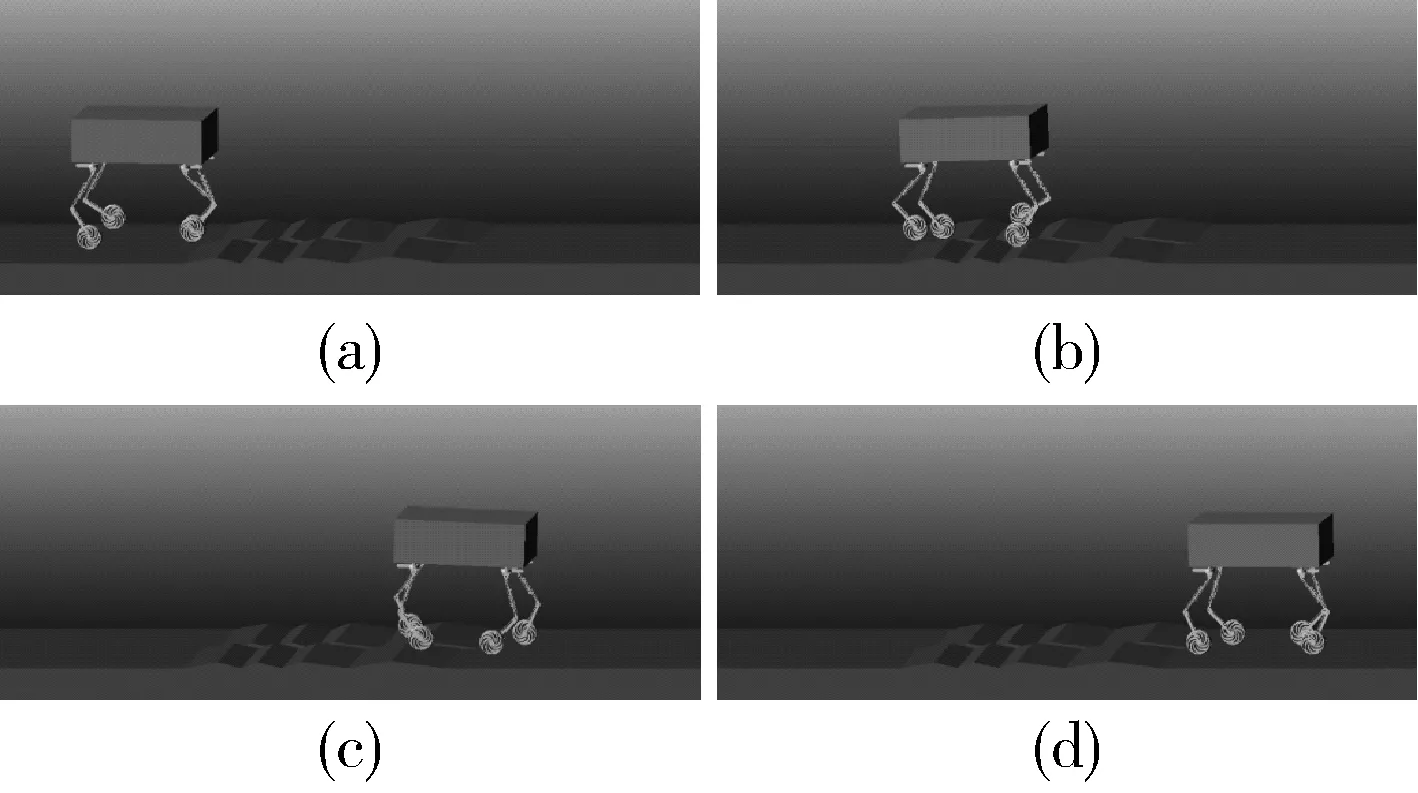
图5 采用主动柔顺控制仿真截图
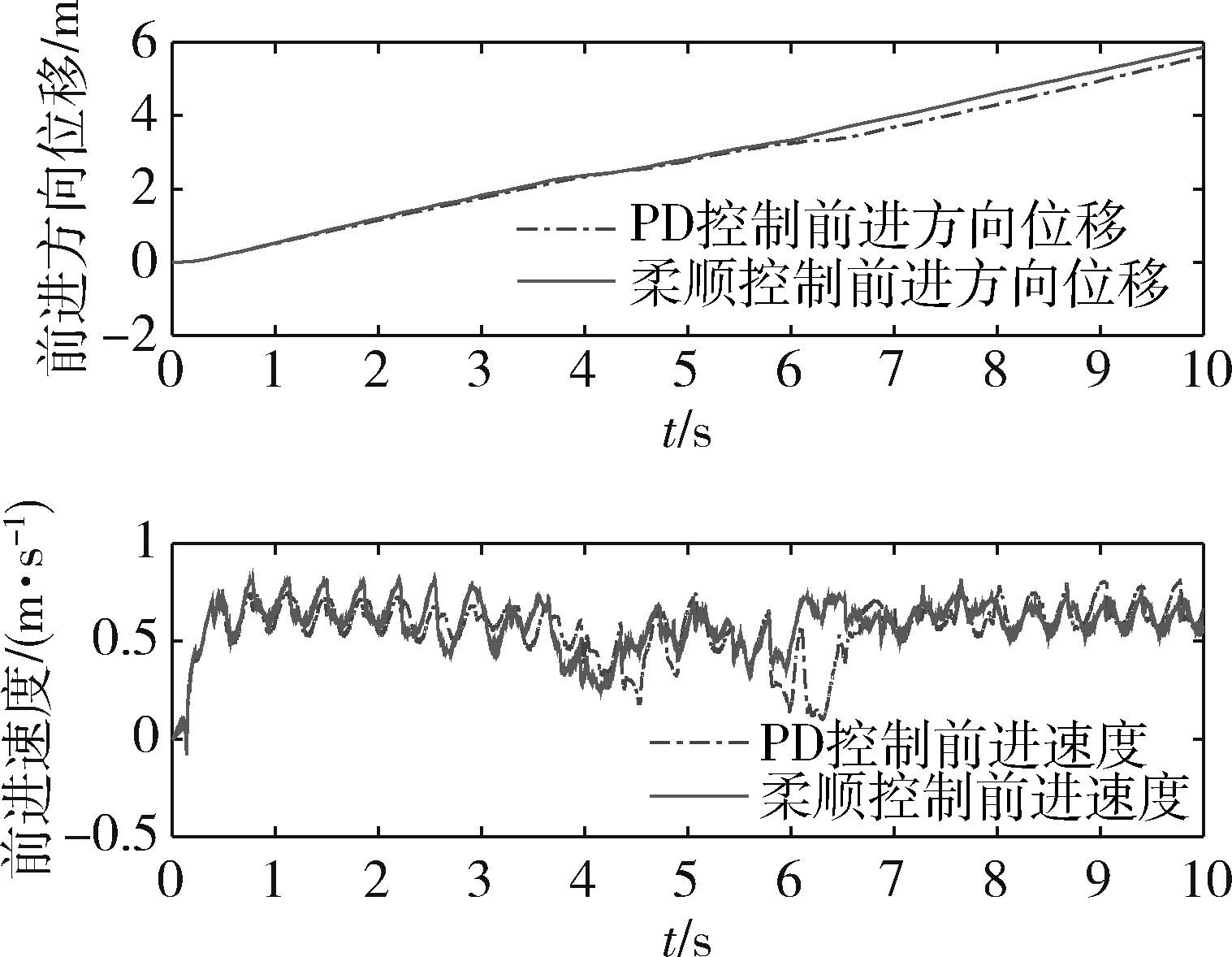
图6 机器人前进方向位移和速度曲线
机身俯仰角和滚转角曲线如图7所示,采用PD控制时,机身俯仰角在±4°内波动,滚转角在-6°~4°内波动,而采用柔顺控制时机身俯仰角和滚转角的波动范围均控制在±2°左右。

图7 机身俯仰角和滚转角曲线
3.2 不平整地形2仿真
仿真中机器人通过一段上下坡的地形,采用主动柔顺控制时仿真截图如图8所示,机器人机身运动轨迹曲线如图9所示,采用柔顺控制时,机器人能够顺利通过上坡和下坡地形,仿真中机器人在3~7s期间上坡,9~13s期间下坡;而采用PD控制时,机器人无法通过该地形,在6s左右机器人向坡下滑落。

图8 采用主动柔顺控制仿真截图
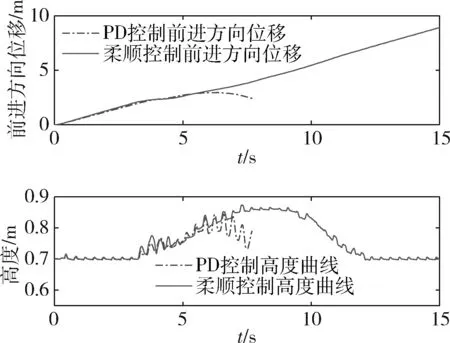
图9 机器人机身运动轨迹
机身俯仰角和滚转角曲线如图10所示,采用柔顺控制时,机器人在上下坡期间机身俯仰角控制在-6°~8°以内,滚转角控制在±5°以内;而采用PD控制时,机器人上坡时机身姿态波动越来越大,在6s左右向坡下滑落。

图10 机身俯仰角和滚转角曲线
为进一步验证本文所提的主动柔顺控制方法中姿态柔顺控制的必要性,继续做下面2组仿真对比,其中一组采用本文提出的主动柔顺控制方案,其中姿态控制为本文提出的姿态柔顺控制,称为柔顺控制Ⅰ;另一组同样采用柔顺控制方法,称为柔顺控制Ⅱ,与柔顺控制Ⅰ相比有2点不同,一是关节空间的阻抗控制中不加入自适应参数,二是姿态控制的腿长调节量不通过阻抗滤波器直接生成支撑腿长度的修正指令,此时姿态控制没有柔顺性。
机器人机身运动轨迹曲线如图11所示,采用柔顺控制Ⅰ时,机器人能够通过上坡和下坡地形,不平整地形对机器人前进速度影响较小,仿真中机器人在3~7s期间上坡,9~13s期间下坡;而采用柔顺控制Ⅱ时,机器人虽然能通过该不平整地形,在机器人前进速度受地形影响较大,前进距离明显小于采用柔顺控制Ⅰ时的前进距离,主要体现在爬坡阶段,仿真中机器人在3~10s期间上坡,爬坡时间接近采用柔顺控制Ⅰ时的2倍。

图11 机器人机身运动轨迹
机身俯仰角和滚转角曲线如图12所示,由图可知,采用柔顺控制Ⅰ时机器人爬坡阶段身体姿态波动小于采用柔顺控制Ⅱ的情况。

图12 机身俯仰角和滚转角曲线
4 结论
提出了一种未知不平整地形下的足式机器人主动柔顺控制方法,使机器人在不需要地形信息的情况下,对不平整地形具有一定的适应能力。该方法融合了基于关节空间的阻抗控制、关节PD控制和姿态柔顺控制3部分,通过综合设计关节柔顺控制和姿态柔顺控制的滤波器参数,结合自适应调节参数,改善了传统阻抗控制的正反馈现象,使机器人在通过不同地形时保持姿态平稳。最后基于虚拟样机仿真平台,分别针对2种地形环境进行对比仿真。对于地形高度落差最大值为6cm的不平整地形,采用本文提出的控制方法后,机身姿态波动的最大值减小50%;对于坡度为10°的上下坡地形,与PD控制和传统的阻抗控制相比,采用本文提出的控制方法后机器人通过不平整地形的平稳性和快速性均有提高。2组仿真结果表明,在不平整地面下机器人可以快速平稳行走,从而验证了提出方法对不平整地形的适应性。
