基于关联控制参数的火箭遥测数据对齐方法

鄢青青 肖 锋 彭宗尧 周 翔

西昌卫星发射中心，西昌615000

多年的火箭发射过程积累了大量遥测测量数据，充分利用它们进行对比分析，有助于故障分析和掌握火箭的飞行特征，并不断改进设计以提高火箭产品的质量。由于火箭飞行过程和时长的差异，历史数据的时间轴对齐是比对分析、包络计算和关联分析等分析判读的基础。

数据对齐多以特征部位为“参照物”实现，如魏书军等[1]介绍了通过在接收端统计数据同步码到达时间差的方式实现FPGA多通道数据自动对齐的方法；李群辉等[2]提出一种以断裂面轮廓曲线为特征的匹配算法以实现碎块对齐；Tomashenko等[3]构建了用于分段的特殊词汇网络(分词网络)以实现快速单通道语音自动对齐；胡阳明等[4]提出的基于改进主动形状模型的三维人脸自动对齐算法通过对二维人脸进行快速自动特征点定位，并根据三维人脸柱面展开的二维纹理图进行自动特征定位并分片，自动实现三维人脸顶点稠密对齐。

火箭遥测数据对齐中，目前应用较多的是按TK指令时间对数据进行分段并局部插值后对齐的方法。该方法在一定程度上减小了全局插值对齐所引起的关键时刻错位，但仍然不能满足精确自动判读的精度需求。为进一步提高数据比对分析与自动判读的准确性，提出一种基于关联控制参数的数据分段和选择性均匀插值的数据对齐方法。实验结果表明，该方法在保持了原数据趋势和形状的基础上，显著降低了关键时刻错位带来的对齐误差，提高了对比分析的直观性。由于数据采集与传输中的干扰因素存在，本文提出的数据分段插值方法应结合野值清除、数据平滑、特征点识别与定位等数据预处理手段使用。

1 基于关联控制参数的数据分段方法

数据分段是按照选定的节点将一个完整测量数据序列，在时间轴上划分成多个代表不同含义或具有不同表现的较短数据段。

火箭遥测数据可分为控制参数数据和非控制参数数据2类。其中控制参数数据是火箭控制系统发出的指令信号，作用于执行机构，实现对火箭飞行状态的实时或相对定时启控。反映温度、压力、角度、转速等信息的非控制类参数采样数据常会根据其关联控制参数改变而发生变化，因此以关联控制参数的有效时间节点(代表着关键的控制事件)作为分段点，可以保证遥测数据(除特别说明外，遥测数据指非控制参数数据)对齐时所关注的主要现象段不发生错位。

考虑确定型和不确定型2类控制参数，其中确定型属于固有飞行时序控制输出，规定了具体的理论控制次数和控制时间；不确定型，一般属于实时、动态控制输出，无理论控制次数和时间，故不同历史过程的遥测数据无法用这类控制参数实现分段对齐。

在火箭的飞行控制逻辑中，很多关键控制事件之间的时间间隔是固定的，如果将它们混入时长不固定的时段内进行统一插值对齐，就会使固定时长段被缩放，从而带来较大的对齐误差，降低比对分析的价值，如图1所示。

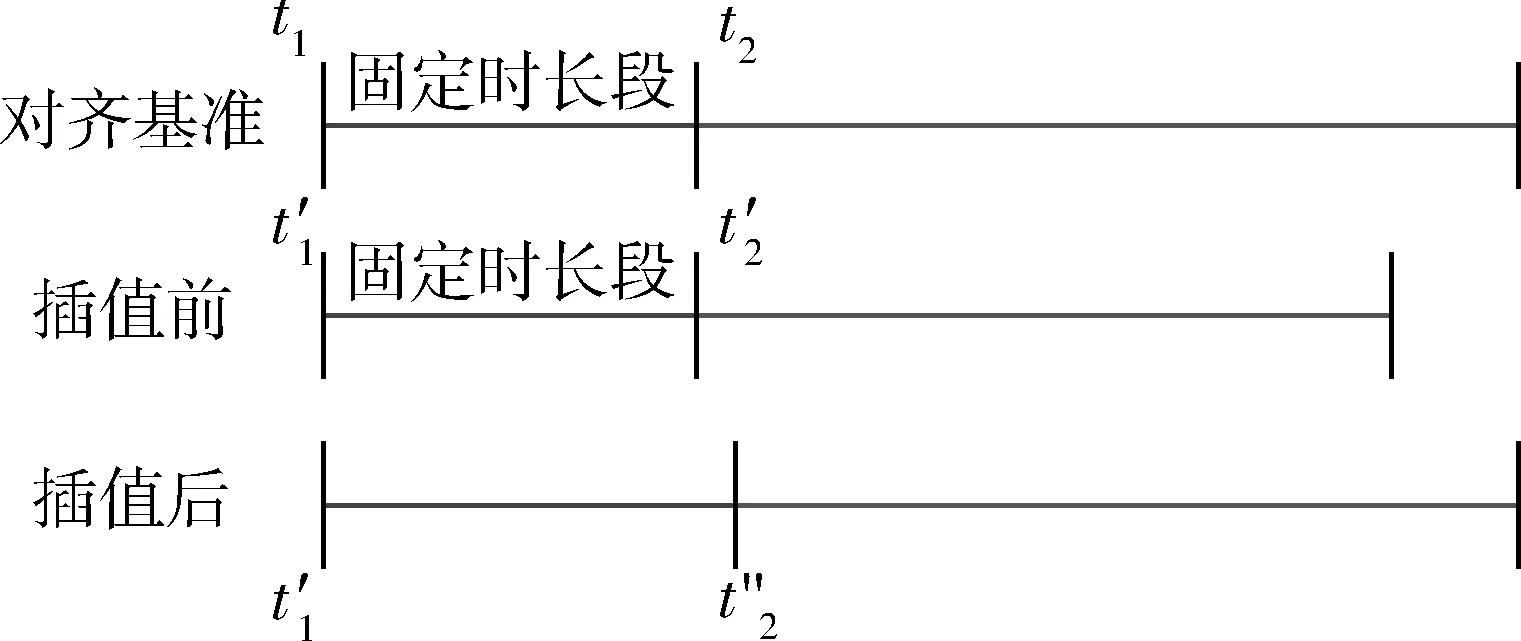
图1 含固定时段的分段插值对齐

设曲线数据序列为L(t)，其确定型关联控制参数集为K={Km|m=1,2,…,M}。其中参数Km可能在多个时刻存在有效的控制指令，即K的采样数据集是一个时间和指令的数据对集K={Km|m=1,2,…,M}={(Tm,n,Km,n)|m=1,2,…,M;n=1,2,…,Nm}，Tm,n表示参数Km的第n个控制指令输出时刻，Km,n=Km(Tm,n)表示Tm,n时刻输出的控制指令。

则满足条件

(1)

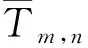
对不确定型控制参数的控制时刻所划分的数据分段而言，虽然变化趋势的比对和历史包络计算已失去价值，但该控制参数作用的有效时段的时长、次数和数据变化幅度等却仍有对比分析价值。如图2所示，某参数P1数据在2次飞行中因不确定型控制参数作用而发生变化的次数相同，被作用时长和变化的幅度却不同，但在未对齐和插值的情况下进行对比分析的直观性较差。

图2 不确定型控制参数分段曲线对比

根据不确定型控制参数的实际作用时段，可将被该控制参数作用的时段分为有效段和无效段，代表被控对象的工作时段和不工作时段，例如气液路电磁阀打开时段为有效段而关闭时段为无效段、伺服机构动作时段为有效段而无动作时段为无效段，如图3所示。

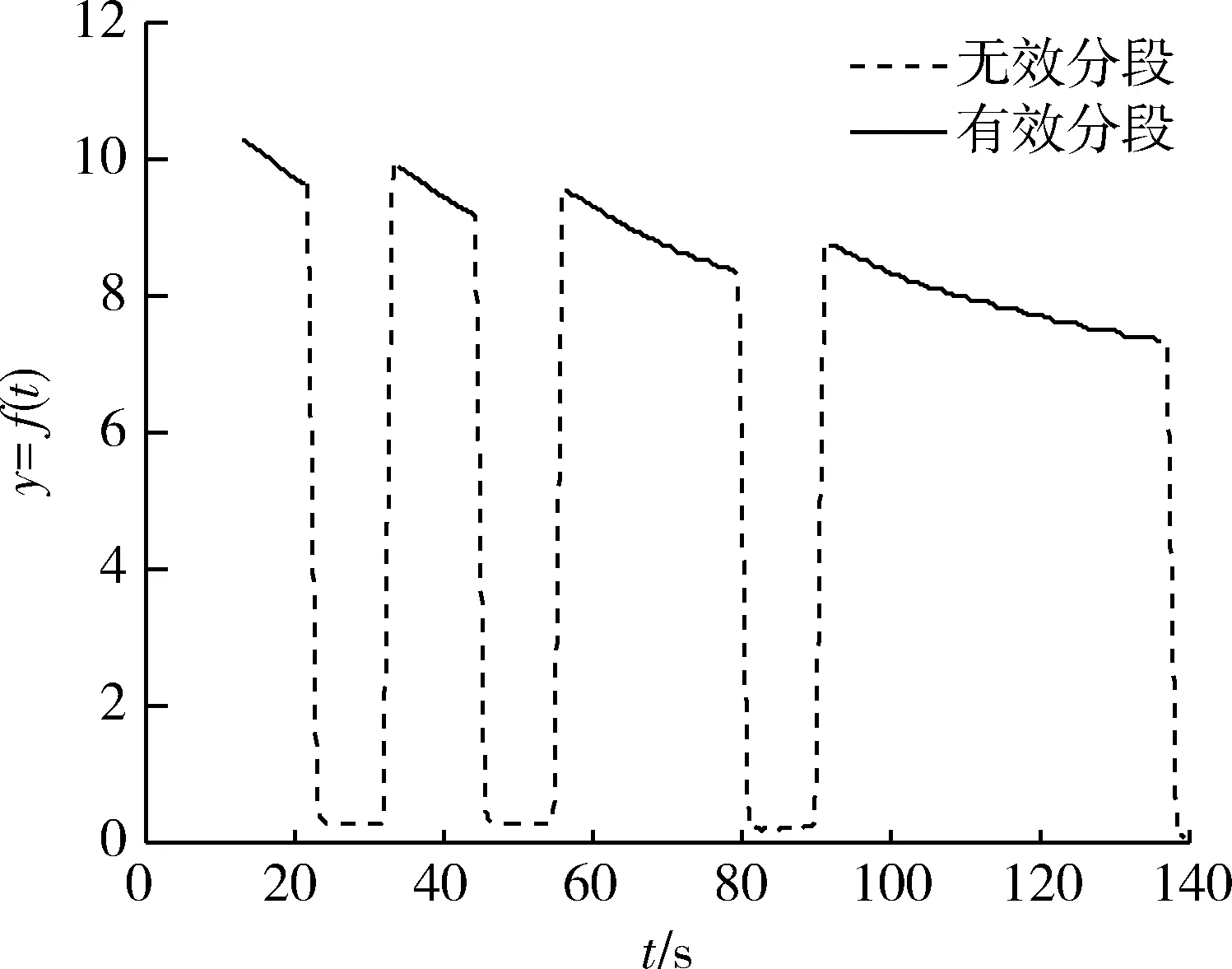
图3 不确定型控制参数分段的有效段和无效段示意

2 分段插值方法

由于火箭测量数据在不同时段具有不同且独立的变化特征，不同分段之间不要求平滑过渡，因此采取各分段内局部插值的方法，在对齐各分段的基础上实现2个数据序列的全局对齐。

2.1 确定型控制参数分段插值

确定型控制参数分固定时长段和不定时长段，仅对不定时长段进行插值。固定时长段按需求决定是否插值，如对比历史数据中某固定时长段控制时间的误差时可不对该段插值对齐，但在计算包络时需插值对齐(正常情况下固定时长段无偏差或仅有微小偏差)。

如图1所示，当需对齐曲线的分段长度小于对齐基准曲线对应的分段长度时，必须对该分段进行插值以填充缺少的数据点，才能使其与基准曲线分段在时间轴上两端完全对齐。但无论是先对齐2个分段的左侧然后对需插值分段的右侧进行插值，还是先对齐右侧再对左侧进行插值，均会导致插值后的曲线特征发生明显非期望的变化，无法用于对比分析和包络计算。如图4所示，图中对比了一个缺少约105s数据的曲线分段的2类左(右)侧插值(3次样条插值)后曲线，即对数据缺少段分别给定1个或2个端点的情况下进行插值的结果。

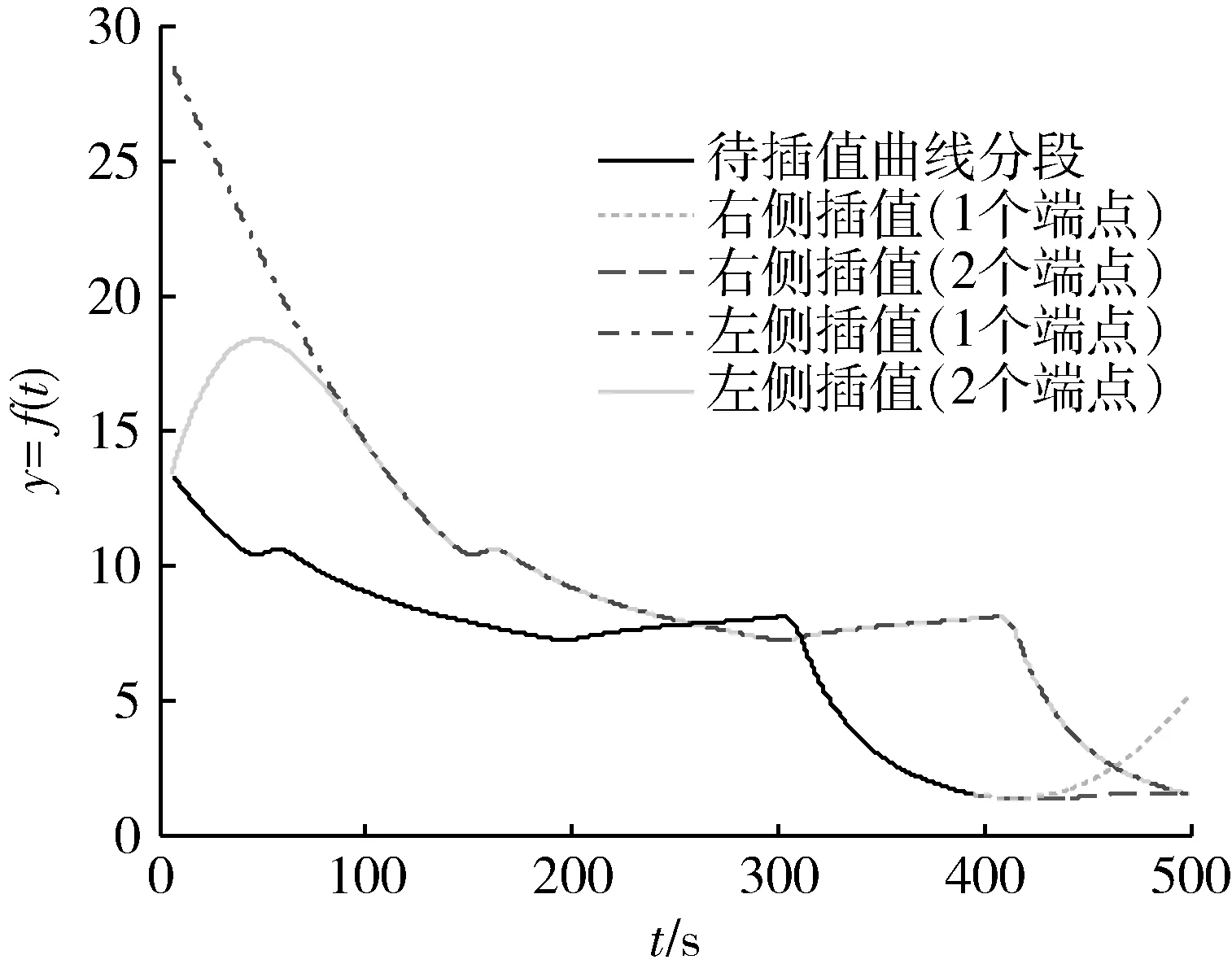
图4 曲线分段两侧插值对比

同时，经过多次插值验证，将整个数据缺少段放入待插值曲线分段的中间不同位置后进行插值对比的结论与上述两侧插值结论相同。故为了获得与原曲线变化趋势和形状尽量一致的插值后曲线，采取一种近似均匀插值的方法：先将缺少数据段按等距分布均匀插入待插值曲线分段后，再进行3次样条插值。

设待插值曲线分段为{L(t)|T1≤t≤T2}，需填充的缺少数据段的长度为C1ΔT，其中C1为缺少数据段的分割数量，ΔT为其每个分割段的长度，则各缺少数据段分割段的插入位置为tc=T1+c(T2-T1)/(C1+1)，其中c=1,…,C1。插入缺少数据段分割段后的待插值的曲线段可表示为

(2)

设L1(t)插值后为光滑曲线，所有相邻数据点之间均为三次多项式函数曲线，两侧端点为非扭结边界，则可用三次样条插值[5](Cubic Spline Interpolation)实现对该分段中数据缺失段的插值。

2.2 不确定型控制参数分段插值

以不确定型控制参数时间将遥测数据分为有效段和无效段，仅对无效段进行插值。将需要插值的数据点均匀分布到无效段内，然后对这些点进行插值，即选择性均匀插值(无效段均匀插值)。

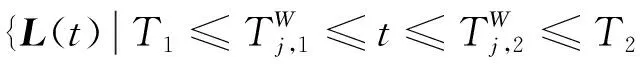
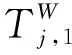
L1(t),T1≤t≤T2+C1ΔT,t∉[H1,H2]

(3)

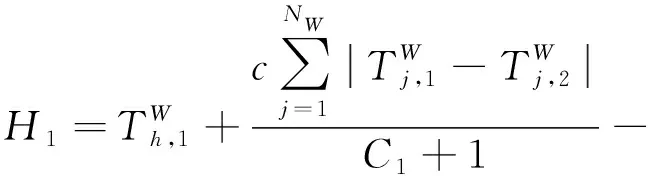
仍然用三次样条插值实现对L1(t)缺少数据的插值。

3 算例分析实验

3.1 确定型控制参数分段插值

式(2)中，C1是确定对原曲线段插入数据分割段数目的参数，其取值直接影响插值的精度。对图4中的待插值曲线分段，通过选取不同的C1，分析其对插值结果的影响，如图5所示。可见当C1取不同值时(C1最大值为缺少数据段的数据点总数)，对L1(t)进行三次样条插值的结果也不同，且C1越大时与原曲线段L(t)变化趋势和形状越一致。

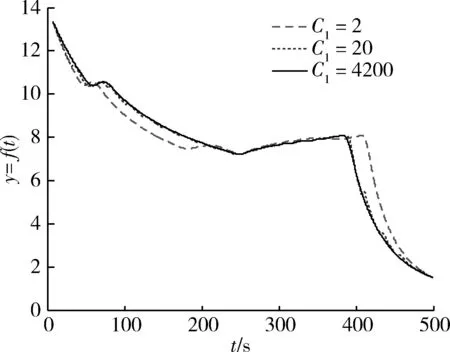
图5 参数C1对插值结果的影响

取某参数在2次飞行的数据Q(t)和L(t)，时长大者为对齐基准Q(t)(见图6)，2次飞行时长之差共115s，每次的遥测数据中均包括4个TK指令，在确定型控制参数作用下分为2个固定时长段和3个不定时长段。

图6 待插值对齐曲线及对齐基准曲线

对待插值对齐的数据曲线，分别采用全局均匀插值、TK指令分段均匀插值(各分段插入时长为55s，35s和25s的数据)和确定型关联控制参数分段均匀插值3种方法进行插值，同时设C1为最大值，均通过三次样条插值后绘制曲线，如图7。由于数据一般在不同时段内具有相对独立的变化趋势和特征，且时段划分时采用关联控制参数时间比采用TK指令时间更准确，故在参数对比分析中，确定型控制参数分段插值获得的曲线比全局插值和TK分段插值获得的曲线发生关键时刻和特征错位的可能性要小。

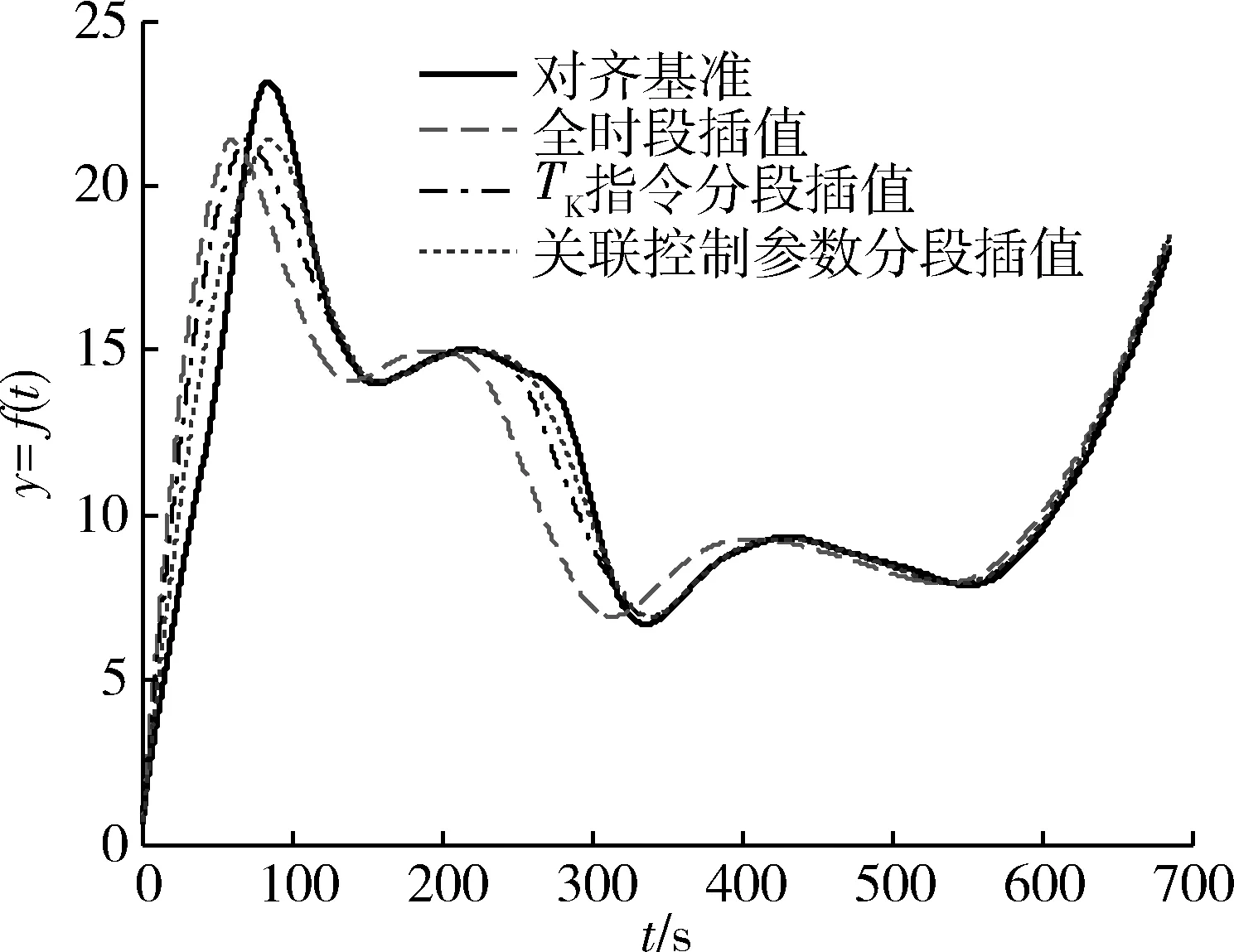
图7 3种插值方式效果对比

可通过计算均方误差[6]来衡量3种插值方式的结果与对齐基准曲线之间的误差。首先通过初值化算子[7]

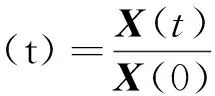
(4)

实现Q(t)和L(t)的归一化处理，得到Q′(t)和L′(t)，并计算它们的均方误差

(5)

由式(5)计算得到3种插值方式结果与对齐基准曲线Q(t)的均方误差见表1，对比可知确定型控制参数分段插值可有效降低关键时刻和关键特征错位带来的误差。

表1 3种插值结果与对齐基准曲线的均方误差

3.2 不确定型控制参数分段插值

式(3)中，C1的取值同样影响插值精确度。如图8可见当C1取值越小时，无效段被插值后出现非期望的、与原曲线无效段趋势不一致的结果的概率越大；而C1取值越大，结果与原曲线中无效段的变化趋势越一致。

对图2所示的参数P1的历史数据曲线进行选择性均匀插值对齐，如图9所示，通过插值对齐后，可见“历史曲线2”比“历史曲线1”在纵轴上的最终下降幅度小，对比分析的直观性比图2强。

图8 参数C1对不确定型分段插值结果的影响

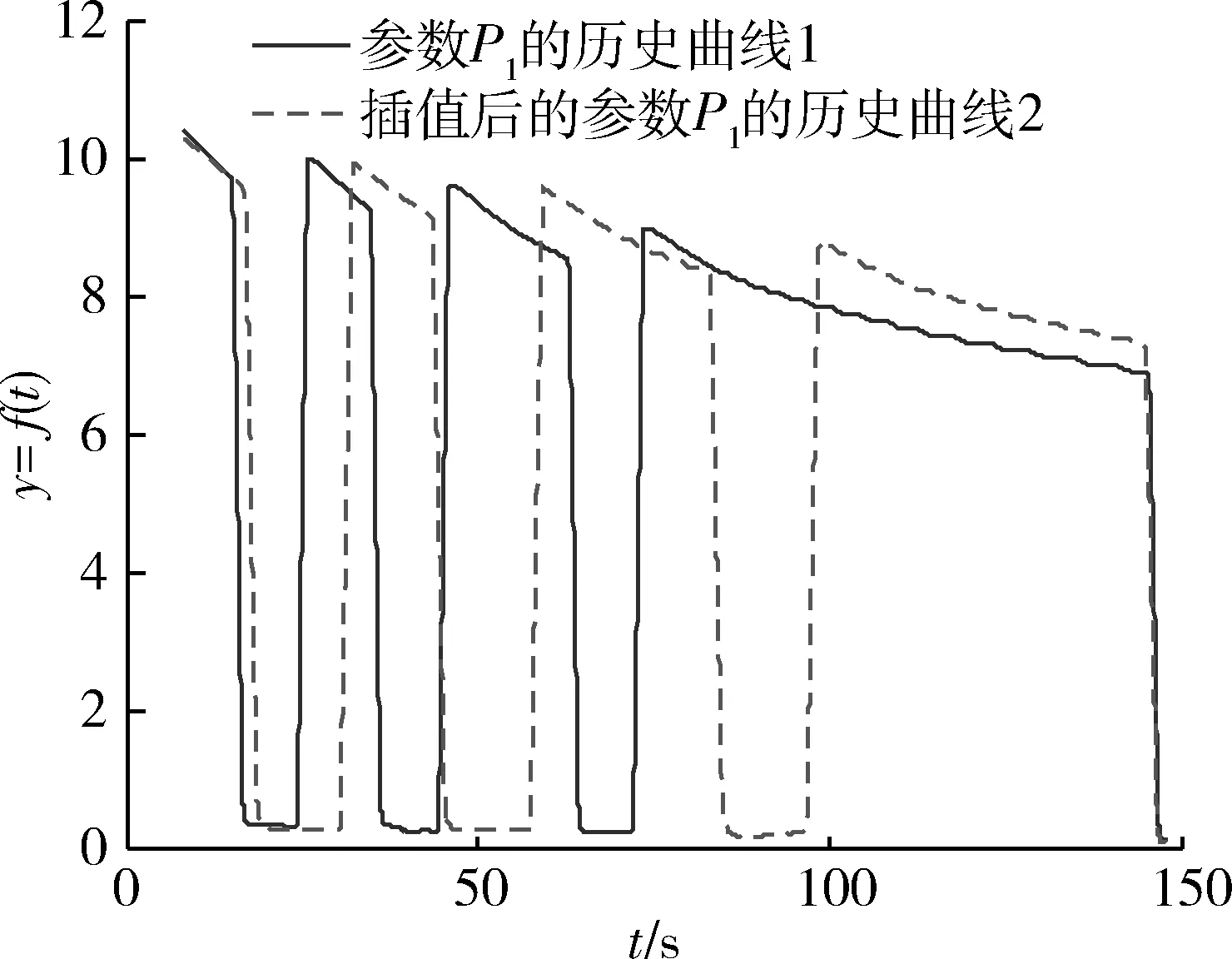
图9 参数P1两条历史曲线插值对齐结果

不确定型控制参数分段一般包含在确定型控制参数分段的不定时长段内。在对这类分段进行插值对齐时，通过选择性均匀插值，既可实现不定时长分段的对齐，又能使不确定型分段内的有效段特征不被缩放，确保了不确定型控制结果对比分析的准确性。如图10所示，与图9插值时长相同时，全时段均匀插值相对选择性均匀插值，对有效段具有明显的缩放作用，改变了数据的关键信息。

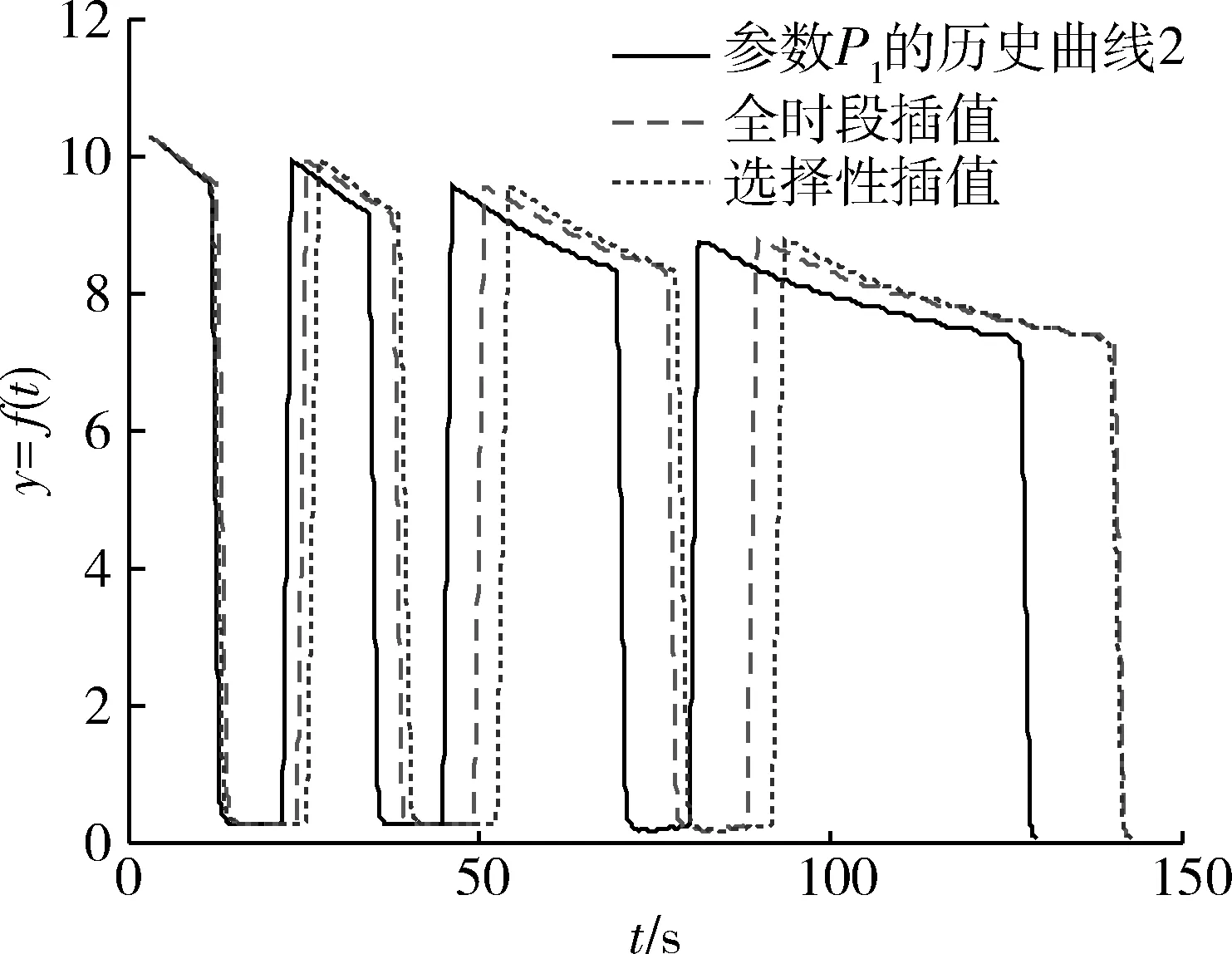
图10 参数P1历史曲线2的两种插值对齐方法效果比较

4 结论

对基于关联控制参数的数据分段，探讨了选择性均匀插值的数据对齐方法，从算例分析中可知，对数据进行插值时，采用基于关联控制参数分段插值的方式比全局均匀插值和TK指令分段插值的精度高；均匀且插入段长最小时可尽量保持原数据形状和趋势不变；采用不确定型控制参数分段插值，在保持控制有效时段不变的情况下，可实现不定时长段的插值对齐，有效提高对比分析的直观性。目前主要针对遥测系统正常的情况下采集和传输的数据，下一步将加强对带有传输盲区数据和稀疏数据的对齐方法的研究。