标准图元数控编程系统及其路径规划算法的研究与设计
2018-11-01程志华吕炘宇
程志华,吕炘宇
(上海大学 机电工程与自动化学院,上海 200072)
0 引言
金属构件常作为连接与支撑件在工程建设方面广泛应用,众多专业从事设计与制造金属构件加工机床的企业中,德国、意大利、日本在这一领域处于领先地位[1],已出现了系列化、高度自动化的专用机床。我国相关行业起步较晚,加工装备大多是普通机床或手动、半自动机械加工设备等通用加工设备。在专用数控系统加工方面,国内研究人员已取得一定成果。如李成华等[2]基于AutoCAD开发了一套图元数控编程系统,解决了图元排序、识别和程序输出问题,但是并未对图元信息进行定义,系统缺乏可扩展性。章勇等[3]基于DXF文件开发了切割加工自动编程系统,解决了开放数据参数问题,但是并未对加工路径进行规划,系统加工效率低。因此,结合幕墙行业的特点,开发行业专用的先进制造设备对提升行业的技术水平具有十分重要的意义。
本文针对图元自动数控编程系统中的关键技术进行研究,以软件工程为实现方法,实现了图元信息的统一以及由图元向G代码的转换。同时,针对遗传算法在实现路径规划的搜索过程中的收敛过慢和容易早熟问题[4],本文采用了将不同适应度种群进行分类的方法,对于不同类别的个体分别采用混合交叉算子和混合变异算子来加快算法的收敛速度,从而改进遗传算法,使其在加工路径规划问题中达到多样性和收敛速度的平衡。
1 系统实现
系统整体设计思路是以IPC作为主机,工控机的CPU与PMAC卡的CPU构成主从式双微处理器开放式模块化结构,系统主要模块规划结构如图1所示。
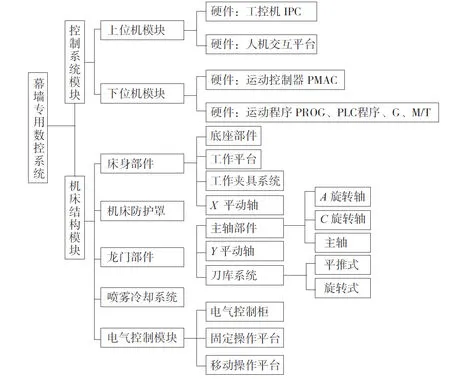
图1 幕墙专用数控系统主要模块规划结构图
其中,上位机模块需完成图元信息的处理、自动数控编程、机床加工路径优化等上层功能,下位机模块需实现伺服计算、插补运算、位置控制、刀具补偿、速度处理以及离散逻辑PLC等实时控制。
2 图元自动数控编程中的关键技术
2.1 图元信息的定义
对于幕墙金属构件所用到的标准图元,其信息可以精简为:主要由基点、坐标系、加工信息和尺寸信息4部分组成。通过对每一个图元所包含的信息进行分析、总结和归纳,得出它们之间的相互关系,发现并提炼出它们的共性,最终实现将各种金属构件的各加工面上所有图元信息统一起来,形成一种标准的图元信息数据结构,如表1所示。

表1 图元后台信息数据结构
2.2 基于模板的程序输出
为了让图元自动数控编程系统输出的数控程序适应加工工艺需求,具有更好的应用性,研究采取基于模板的图元数控程序输出方式。预先在系统中定制多种加工循环的代码模板,根据自定义的图元数据结构,实现对不同图元的加工(模板中存在常量和变量两种数据,常量包括程序头中和程序尾中的固定 G96,M03,M30 等代码,变量包括: 转速,进给,刀具,刀具轨迹点位等。图元尺寸和阵列参数设计软件窗体如图2所示,图3为钥匙孔型图元的模板加工示例)。
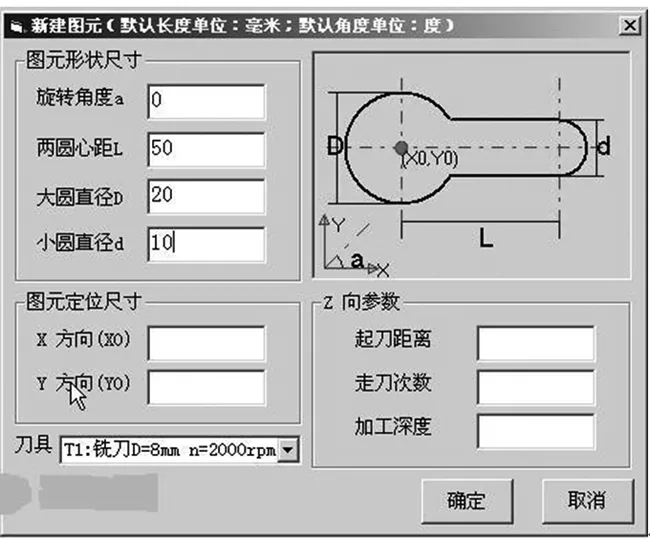
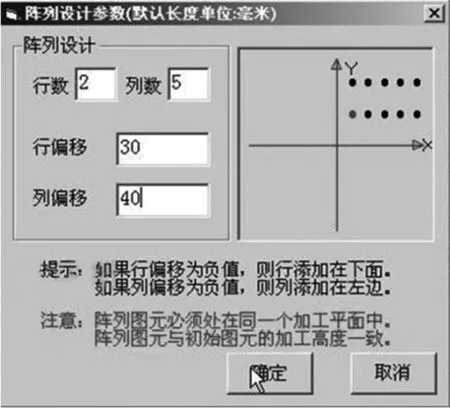
图2 图元信息输入模块和图元阵列设计模块
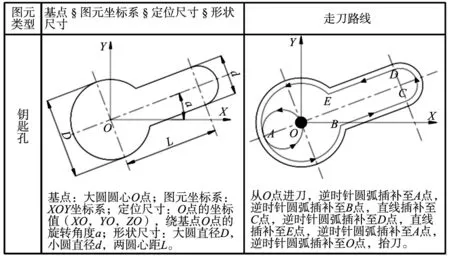
图3 基于模板的程序加工示例
3 基于遗传算法的加工路径规划
在CAD/CAM集成系统中,走刀路径的规划对加工工艺和数控代码的生成都有重要影响。通俗讲,对加工路径进行规划的目的是:在加工金属构件的各待加工面上的一系列异形孔,获得一条最优或次优的加工路径,让刀具在整个加工过程中空行程最短(或尽可能短)、主轴姿态变换和换刀次数最少。
在路径规划问题中,简单遗传算法具有收敛速度慢,易于陷入局部最优解的特点,所以,遗传算法中一个较难解决的问题是如何较快地找到最优解并防止“早熟”收敛问题。
3.1 编码
本文算法采用加工路径表示形式进行编码,其中图元按加工的顺序进行排列,编码串(x1,x2,…xn)表示从图元x1开始加工,依次加工图元x2,x3…xn,最后回到起始图元x1。例如对于路径 4- 3- 5- 6- 1- 2- 7,可简单表示为(4 3 5 6 1 2 7),表示从4号图元开始加工,依次加工3,5,6,1,2,7然后回到4的一条加工路径。
3.2 适应度函数
由于所求为加工路径最短,即最小值问题,因此将算法中某一个体x=(x1,x2,…xn)的适应度值定义为个体所代表加工路径a的距离,即:
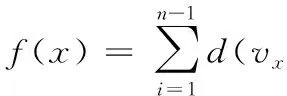
(1)
其中,vx(i)为个体x所代表的加工路径a上的第i个图元。d(vx(i),vx(j))为两点间的距离,而且d(vx(i),vx(j) )=d(vx(j),vx(i))。
3.3 群体的分级
为求函数优化问题最小值为例进行动态分级。设将群体分成k级,记,
f(x*1)=max{f(x1)},f(x*2)=min{f(x1)}
(2)
(3)
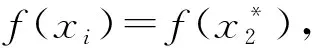
3.4 选择算子
在进行选择操作时,应使个体被选中并遗传到下一代群体中的概率和这个个体的适应度大小相关,适应度大的个体,被选中的可能性就越大。反之,适应度值越小的个体,被选中的概率就越小。
设群体大小为n,其中i的适应度值为fi,则i被选择的概率为:
(4)
3.5 混合交叉算子
对群体进行分类后,基于不同的适应度等级进行杂交操作(级别较低的个体采用常见的部分匹配杂交算子PMX,级别较高的个体采用启发式杂交算子)。对于种群中两个父代个体X=(x1,x2,…xn),Y=(y1,y2,…yn),通过启发式交叉算子产生两个子代个体a1,a2的步骤如下:
(1)随机选定一个图元c作为交叉的起点,初始化子代个体的代码串使它们仅包含一个图元c,并将X、Y中的图元c删除;
(2)找到X、Y中图元c的下一个图元cR1、cR2(将X、Y当作一个环处理)。计算图元c与cR1、cR2的距离d1、d2。
(3)如果d1≤d2,则将cR1加入到a1,并将X、Y中的图元cR1删除;如果d1>d2,则将cR2加入到a1,并将X、Y中的图元cR2删除。
(4)如果此时X、Y的图元数目为1,则直接将该图元加入到a1后结束,否则转(2)重复执行。
同理,将上述(2)~(4)的相关操作改为查找c在X、Y中的的前一个图元cL1、cL2,由图元c与cL1、cL2的距离来决定选取,可生成另一个子代个体a2。
3.6 混合变异算子
同理,对群体进行分类后,基于不同的适应度等级进行变异操作。级别较低的个体采用常见的2-opt交换变异,级别较高的个体采取了如下的一种启发式倒位变异算子。
启发式倒位变异算子的基本思想是首先随机选择一个图元c,然后在除c、cR、cL外的其他图元中选距离c最近的图元c′,再对cR到c′之间的图元进行倒位。例如对一个随机父辈个体P(6 2 5 4 3 1),若随机选择一个图元2,离图元2最近的图元有4和3,若选择图元4作为第二点,则产生新个体a1(6 2 4 5 3 1),若选择图元3作为第二点,则产生新个体a2(6 2 3 4 5 1)。这种方法考虑了原有边的邻接关系,将巡回路线上的优良性能很好地遗传到了下代的群体中,因此提高了算法的收敛速度。
3.7 实验结果分析与比较
对本文算法,设定群体规模采用60,分为4级,而每级产生的下一代个体数目分别为60、90、120、150。以51个坐标的问题为例,算法运行的路径如图4、图5、图6所示:当运行代数分别为5、10、20时,算法所得最终距离分别为437.3、431.5和428.8。
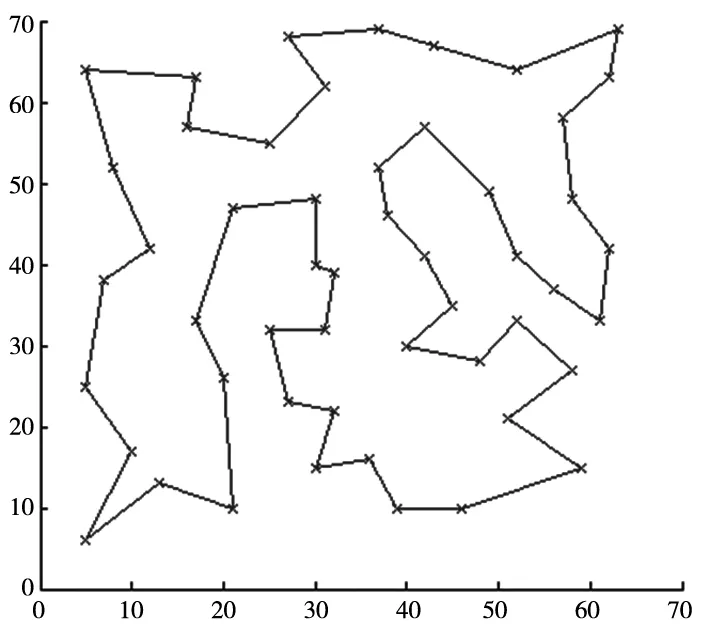
图4 T=5,length=437.3
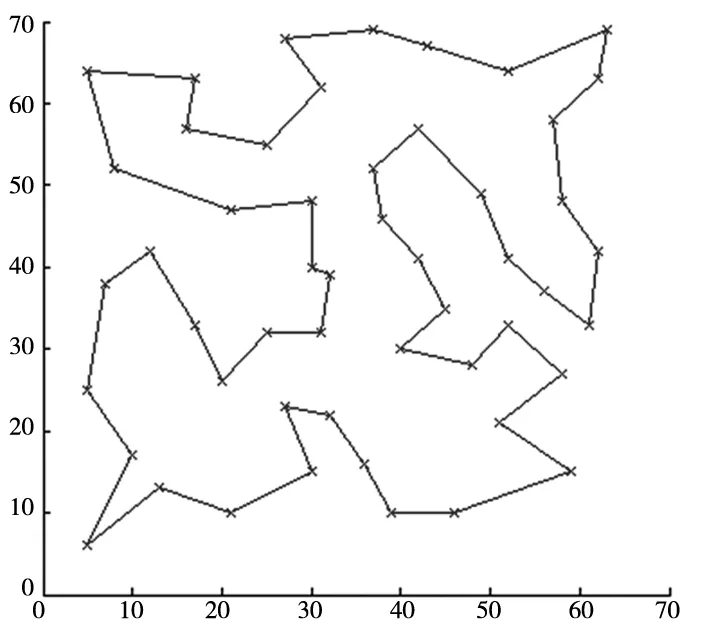
图5 T=10,length=431.5
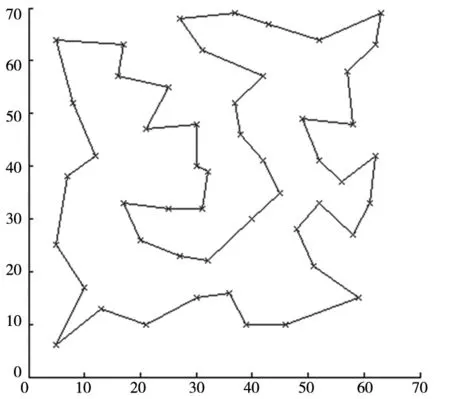
图6 T=20,length=428.8
实验结果表明,实验获得的最优解要接近于TSPLIB问题库中给出的最优解,见表2。

表2 实验结果对比
图7为综合本文算法和结论所得的图元自动数控编程系统软件主界面及加工路径规划示例。

图7 图元路径规划示意图
4 结论
本文针对幕墙金属构件的标准图元,设计了一套自动数控编程系统。重点阐述了图元数据结构的定义方法和基于改进遗传算法的加工路径规划方法。机床应用结果表明,该系统具有较高的加工效率,各项基本功能满足设计要求。
