基于LCA的机械产品绿色设计中材料优化选择评价研究

韩珍玉

(中原工学院信息商务学院，郑州 450000)

0 引言

当今社会，随着资源短缺与环境污染问题的日益严重，人们的绿色意识不断增强，特别是在高能耗、高污染的制造业中，绿色设计等先进思想越来越受到重视。作为绿色设计的首要环节，材料的合理选择是实现产品绿色化的关键所在。

与传统设计选材不同，绿色设计中的选材是基于对材料生命周期分析(LCA)过程后进行的，不仅考虑机械产品的材料从原材料开采、成品材料的制备到产品的制造、使用及报废后材料的回收再利用整个生命周期过程的机械、工艺、经济性能，而且将材料整个生命周期中对环境的影响作为一个重要因素加以考虑，如图1所示。目前常用于绿色设计中的选材方法包含模糊层次分析法、模糊综合评价法、三维指标法等。这些方法多次被设计人员运用到材料选择的研究当中并取得了一定的成果。例如，李磊等将模糊层次分析法运用到机械材料的选择当中[4]；张丹丹等运用三维指标法，将材料的技术性、经济性及绿色性作为三个坐标方向，建立一个三维空间坐标系来研究绿色设计中选材的关键技术[5]。但是他们所采用的选材方法都过于单一，容易放大该方法的缺点，影响选材准确性。本文建立了基于LCA的材料选择评价指标体系，运用层次分析法(AHP)及熵权法求得主客观综合权重，最后利用理想点法(TOPIP)确定最优材料方案。该方法在确定权重时较好的融合了AHP及熵权法的优点，即将专家的主观判断融入当中，又有客观数据作为支撑，能够最大程度准确反应各个指标的重要性，对于机械产品材料的选择更具适用性。

图1 绿色设计中机械产品材料选择LCA过程

1 基于LCA评价指标体系的描述

1.1 评价指标体系中相关变量的描述

绿色设计中材料选择的本质是方案的优化问题，即从备选的若干材料方案中选择出最优方案。其备选材料方案可表示为S：

S=[S1，S2，…，Sm]T

其中，m表示备选材料的个数，Si(i=1,2，…，m)表示第i种备选材料方案。

因为本文对材料进行选择是基于对材料生命周期分析(LCA)后进行的选材，即从材料全生命周期中的机械性能、工艺性能、经济性能及环境协调性能4个方面建立评价指标体系。因此，指标层可表示为C：

C=[C1,C2,C3,C4]T

其中，C1—机械性能，C2—工艺性能，C3—经济性能，C4—环境协调性能。

指标层下方对应的子指标层可表示为F：

F=[F1,F2,…Fn]T

其中，n代表子指标的个数，Fj(j=1,2,…n)表示第j个子指标。

1.2 评价指标体系的建立

建立材料选择评价指标体系的目的在于从符合要求的材料中选择出在其整个生命周期过程中具有良好机械、工艺性能，经济成本最低且对环境影响最小的材料。本文结合图1及1.1节中的相关变量的描述，从材料的机械性能、工艺性能、经济性能及环境协调性能:4个方面对材料进行综合评价，并将上述4个指标进一步细化为若干子指标，最终建立了基于LCA的机械产品绿色设计中材料选择评价指标体系，如图2所示。从图2不难看出绿色设计中所选材料的机械性能及工艺性能各子指标主要涉及材料开采、制备及零部件加工制造阶段；而材料的经济性能及环境协调性能各子指标则基本涵盖材料全生命周期的各个阶段。

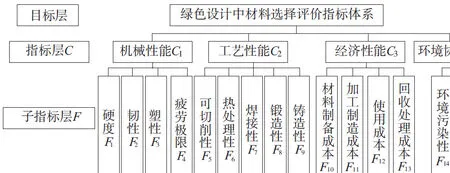
图2 基于LCA的机械产品绿色设计中材料选择评价指标体系

2 评价指标体系的求解

由图2可以看出，机械产品绿色设计中材料选择评价指标体系具有明显的层次结构，因此通常会采用层次分析法(AHP)来求解各指标的权重。但是考虑到该方法的缺陷，若只采用AHP这一单一方法会增大人为主观因素的影响。文章采用AHP与熵权法相结合求得各指标主客观综合权重，可以有效的避免人为主观因素过大对评价结果造成的影响，最后利用理想点法(TOPIP)求取各备选材料方案与最理想材料方案之间的贴进度，并根据数值大小确定最优材料方案。

2.1 层次分析法

(1)构造判断矩阵。针对上一层次中的某一指标Hi，通过比较本层次中与其对应的各个子指标之间E1、E2…En之间的重要程度，得到判断矩阵R。如表1所示。

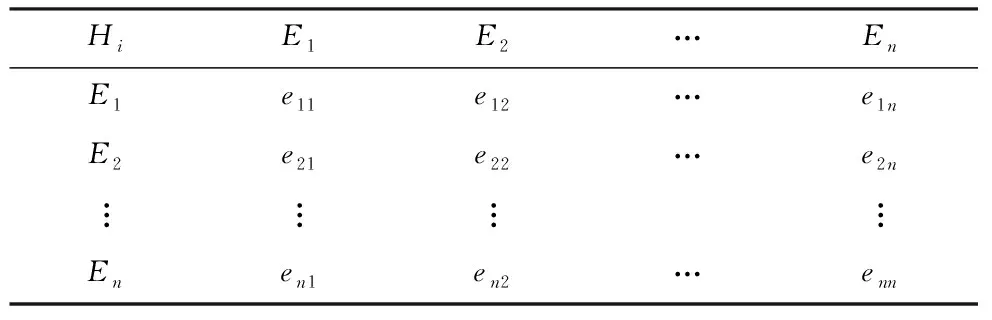
表1 判断矩阵R

本文采用en/5标度法进行数量标度，如表2所示。与传统的1-9、0.1-0.9 标度法相比，该方法具有更好地一致性[6-7]。

表2 en/5标度法及定义

此外规定，如果i指标对j指标的重要程度为eij，则1/eij即为j指标对i指标的重要程度。

(2)层次单排序。层次单排序就是指标体系中针对某一层特定指标其所属下层子指标的重要性排序。其计算过程即为计算该判断矩阵的最大特征值λmax和对应的特征向量M=[m1,m2……,mn]T。其中λmax用于检验判断矩阵的一致性，M则用来计算相对权重向量α,α和M中对应元素满足如下关系。

(1)

(3)一致性检验。一致性检验就是检验矩阵中各要素之间重要性的判断是否合理。根据公式(1)求得的相对权重向量只有满足一致性要求才会有效，如果不满足一致性要求则需重新构建判断矩阵。本文根据计算出的CR来检验判断矩阵是否满足一致性要求，其计算公式如下所示：

(2)

其中，CI为一致性指标，与判断矩阵的最大特征向量λmax有关，其计算公式如下所示：

(3)

RI为平均一致性指标，其取值与判断矩阵阶数的关系如表3所示。

表3 平均一致性指标RI

显然，当n=1,2时，判断矩阵符合一致性要求，而当n≥3时，只需满足CR<0.1，即可认为判断矩阵符合一致性要求[8]。

(4)层次总排序。层次总排序就是将指标体系最底层的指标进行重要性排序。假设该层次指标体系一共有K层(目标层为一层)，则最底层总权重α计算公式为：

αj=α(k)α(k-1)...α2

(4)

其中,j=1,2…n。

2.2 熵权法

熵权法主要包括熵值及熵权的计算，主要用于确定指标的客观权重。在具体实施过程中，根据各指标的离散程度，计算出信息熵的值，进而求得各指标的熵权值。其具体计算步骤如下所示：

(1)构造原始数据矩阵X。将所有待评价方案评价指标的具体数值构成如下的原始数据矩阵。

其中，m、n分别为待评价方案和评价指标的个数。

(2) 对原始数据矩阵X进行标准化处理。通常情况下不同指标的量纲和单位会有所不同，为确保评价的准确性，指标都需要经过标准化处理后才能使用，因此按指标所含的信息分为越大越优型指标和越小越优型指标，它们的标准化处理如下：

越大越优型指标：

(5)

越小越优型指标：

(6)

其中,i=1,2…m；j=1,2…n。

经过标准化处理后得标准化矩阵Y=(yij)mxn，其中yij为第i个方案中的第j个指标的取值，显然标准化处理后yij总是越大越好。

(3)求解特征比重Pij。

(7)

其中，0≤pij≤1，i=1,2…m；j=1,2…n。

(4)计算各指标的熵值Ej

(8)

其中,j=1,2,…n，0≤Ej≤1。

对于信息自由度无限大的系统，其信息熵最大，Ej=1。如果pij=0,则规定pijlnpij=0,Ej=0。

(5)根据上文信息熵的计算公式(8)，得到待评价体系各个指标的信息熵E1，E2，…Ej，j=1,2,…n。

通过信息熵E1，E2，…Ej求得各指标权重为：

(9)

其中,j=1,2，…n。

结合AHP求得的主观权重αj与熵权法求得的客观权重βj，运用乘法合成归一法求得主客观综合权重wj，计算公式如下所示：

(10)

其中,j=1,2，…n。

2.3 理想点法

理想点法(TOPSIS)是一种典型的用于解决多目标决策问题的方法。该方法是将有限个待评价方案与最理想目标进行比较，然后按照各个方案与最理想目标之间的距离大小进行排序。其中最理想化目标分为最优目标和最劣目标。最优(劣)目标就是在所提供方案基础上假定的最优(劣)方案。最优(劣)目标中每个指标的取值都是所提供方案中最优(劣)指标的取值。在所提供的方案中，最优方案必定是距离最优目标最近并且距离最劣目标最远的那个方案。运用理想点法明显提高了多目标决策问题的科学性、合理性和可操作性，在一系列评价选择问题中得到了广泛的应用。

(1)构造加权标准化矩阵V。

(2)求正、负理想点集V+、V-。

其中,

(11)

(12)

其中，i=1,2，…m。

(4)计算贴近度Ii,并根据贴近度Ii确定最优方案。贴近度是指各待评价方案与理想目标之间的贴近程度。根据贴近度确定各待评价方案之间的优劣顺序。其中贴近度最大的为方案为待评价方案中的最优方案。

贴近度Ii的计算公式为：

(13)

其中,i=1,2，…m。

在本文中贴进度Ii越大，其所对应的备选材料方案距离最理想目标越近，越符合设计要求。

3 实例

某工厂要加工制造一批减速器高速轴。技术人员按照其工作环境、负载(该减速器高速轴在常温下工作，载荷中等)等要求，根据相关专家经验及设计中相关校核公式获得满足要求的备选材料方案为45钢、40Cr、42SiMn、20CrMnTi。现从全生命周期绿色设计的角度选择出最优材料方案。

3.1 利用AHP确定材料选择时各指标的权重

根据表2en/5标度法，结合该领域五位专家的意见，对材料的机械性能、工艺性能、经济性能、环境协调性能进行两两比较，得到判断矩阵R如表4所示。

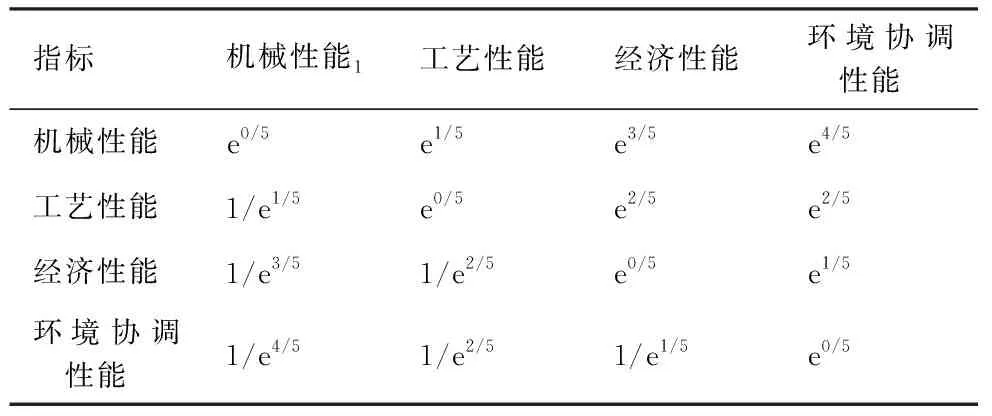
表4 指标层判断矩阵R

求得该判断矩阵R的最大特征值λmax及对应的特征向量后，结合公式(1)求得各指标权重向量α=[0.3569 0.2783 0.1959 0.1689]。由公式(2)、公式(3)求得CR=0.0019<0.1，满足一致性要求。

对于机械性能指标C1对应的子指标构造的判断矩阵R1，如表5所示。

表5 机械性能指标对应子指标判断矩阵

经计算求得各子指标权重α1=[0.2230 0.2229 0.1479 0.4062]，且CR=0.0112<0.1，满足一致性要求。

用同样的方法分别求得工艺性能C2、经济性能C3、环境协调性能C4指标所对应子指标的权重向量，满足一致性要求后根据公式(4)求得总权重如表6所示。

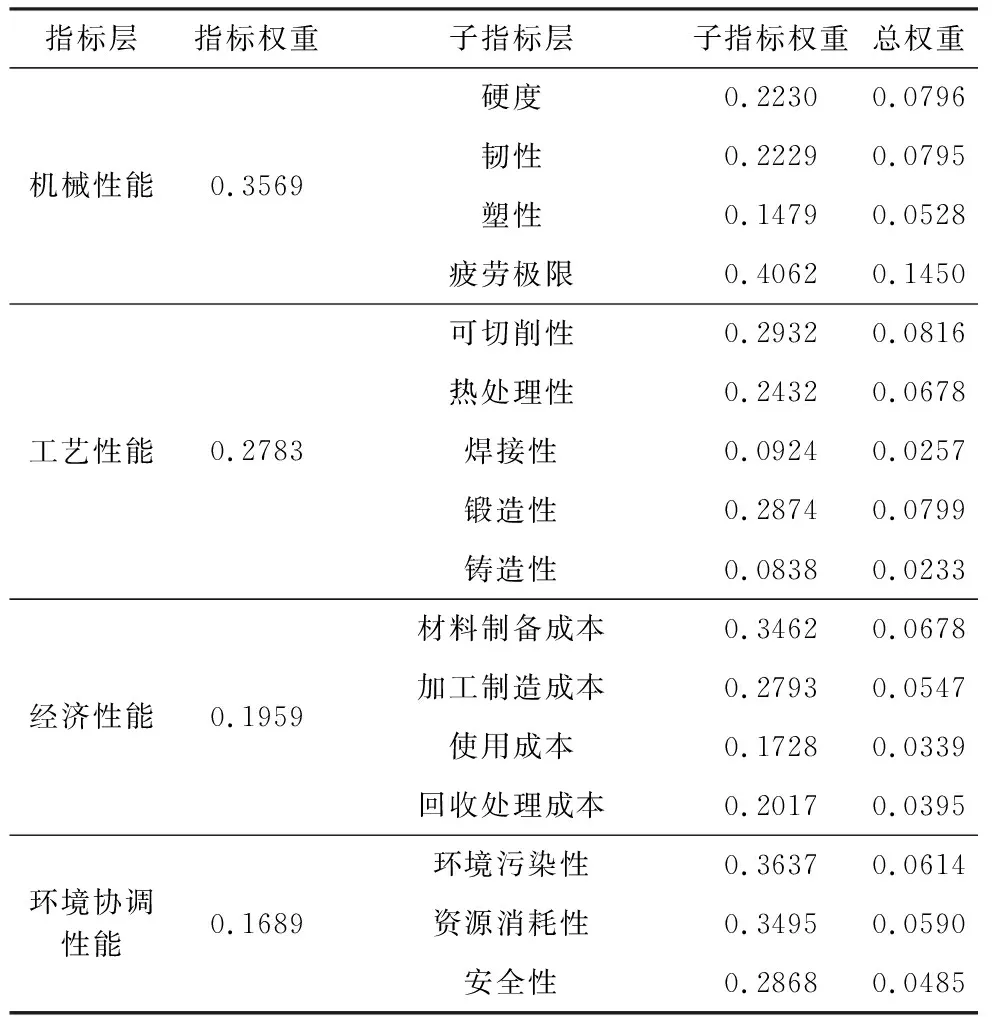
表6 AHP求得的指标总权重

3.2 利用熵权法确定材料选择时各指标权重

首先对4种备选材料对应指标的原始数据进行收集，如表7所示。

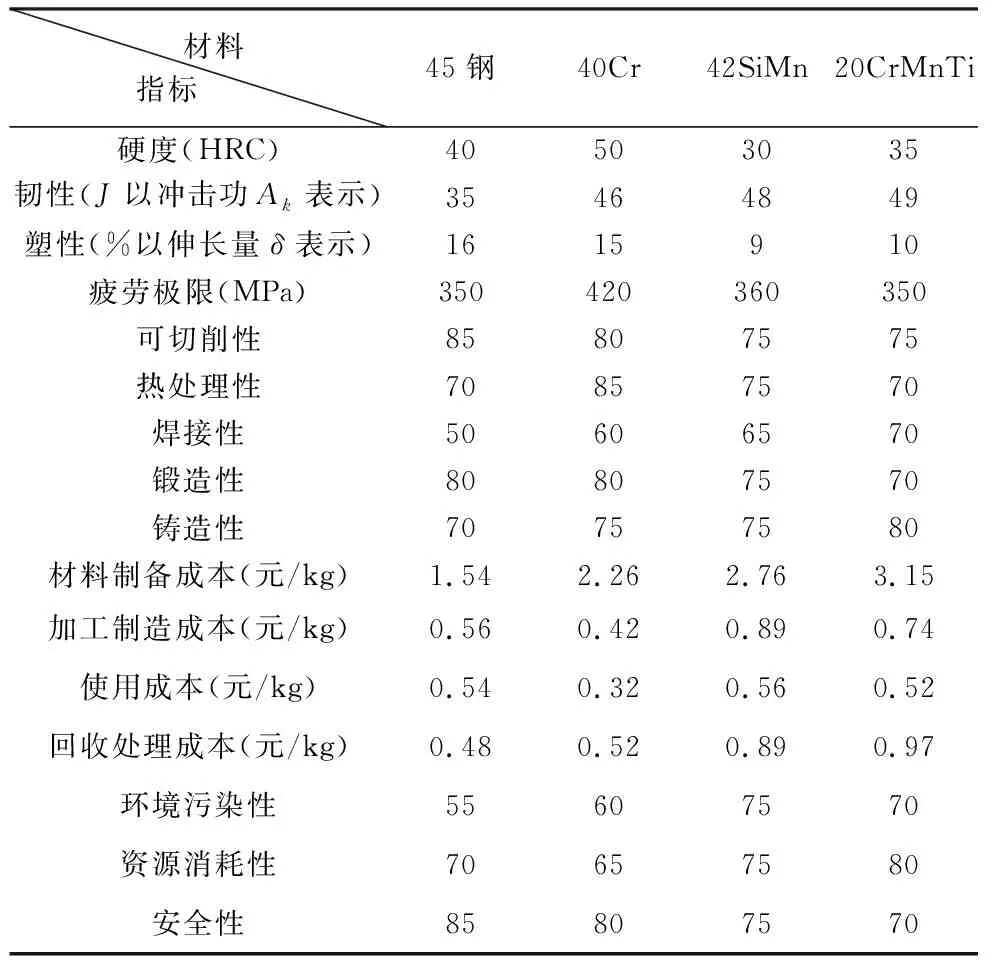
表7 各备选方案指标原始数据

对于上述指标中的定性指标(可切削性、热处理性、焊接性、锻造性、铸造性、环境污染性、资源消耗性、安全性)没有可以直接收集的原始数据。本文采用百分制法，综合几位专家意见，对其进行打分。其中可切削性、热处理性、焊接性、锻造性、铸造性、安全性属于越大越优型指标，其分数越高说明其性能越好；环境消耗性、资源消耗性属于越小越优指标，其分数越低说明其性能越好。

对收集到的原始数据矩阵由式(5)～式(9)求得各指标权重β=[ 0.0528 0.0359 0.0598 0.1436 0.0919 0.1010 0.0399 0.0406 0.0425 0.0524 0.0465 0.0930 0.0580 0.0505 0.0459 0.0459]。

3.3 确定主客观综合权重向量W

根据3.1节、3.2节求得主观权重向量α向量和客观权重向量β后由公式(10)求得综合权重向量W=[0.0598 0.0406 0.0450 0.2966 0.1068 0.0975 0.0146 0.0462 0.0141 0.0506 0.0362 0.0449 0.0326 0.0442 0.0386 0.0317]。

3.4 利用理想点法确定最优材料方案

表8 备选材料方案到理想点的距离及贴进度

由表8可知，各备选材料方案的贴进度I2>I4>I3>I1，即40Cr贴近度最高，所以从材料全生命周期绿色设计的角度，建议选择40Cr作为减速器高速轴的材料。

4 结束语

机械产品绿色设计中材料优化选择评价是基于材料选择LCA过程进行的，不仅对材料的机械性能、工艺性能和经济性能进行分析，而且将材料的环境协调性能纳入其中，作为重点考虑的因素，并建立其评价指标体系。随后提出一种将AHP与熵权法相结合得到主客观综合权重，再运用理想点法确定最优材料方案的方法，最后结合减速器高速轴的选材，验证该方法的可行性。该方法较好的解决了机械产品绿色设计中选材绿色化程度低的问题，但是在具体实施过程中，涉及大量数据的收集及计算，因此为增强其实用性，建立材料数据库，开发材料评价系统是对其进行进一步研究的方向。

DOI：10.1016/j.ejor.2016.08.053.