理想条件下BTA钻钻杆的涡动分析
2015-12-13魏旭民
魏旭民
(中北大学机械与动力工程学院,山西 太原 030051)
引言
在深孔钻削加工过程中,BTA 钻的钻杆在切削液中高速旋转,内排屑设计的BTA 钻杆将受到刀具惯性力、切削力,离心力、切削液的非线性流体力等的综合作用,会引起钻杆的质量偏心问题,从而产生涡动效应,因此钻杆的动力学特性对BTA 刀具的使用寿命以及深孔加工的质量有着十分重要的影响[1]。
1 BTA 钻钻杆的涡动分析
由于在加工过程中切削液、切屑以及切削力的波动影响,工件内孔轴线与钻杆轴线不再重合,会出现质量偏心问题[2],钻杆的运动状态示意图如图1所示。在深孔钻削过程中BTA 钻的钻杆轴线总是偏离工件孔轴线,其偏心距为e、钻杆与工件孔最大间隙为Cmax,最小间隙为Cmin,因此平均间隙为C=(Cmin+Cmax)/2。
BTA 钻钻杆在钻削的过程中由于自身的惯性以及不平衡扰动的作用,使钻杆中轴线被迫偏离原来轴线中心,但钻杆依然绕自身轴线旋转,同时转子(钻杆)还绕着初始轴线做旋转运动,这种现象称之为涡动。通常工件内部的钻杆有两种涡动情况。一种是接触式涡动,即在切削力的波动分量、切削液扰动、切屑冲击以及钻杆弯曲等因素的影响下,工件孔壁与钻杆接触。另一种为非接触式涡动,涡动情况为钻杆中轴线偏离加工轴线,工件孔壁和钻杆间钻削液形成楔形分布的压差,作用于钻杆并将其托起,从而达到新的平衡,而且在此过程中钻杆始终不与工件内孔接触。

图1 钻杆的运动状态示意图
在切削力的波动分量、切削液扰动、切屑冲击以及钻杆弯曲等影响下,钻杆与工件孔壁接触,忽略钻杆与工件内孔间的相对滑动,将内孔沿径向展开,则可看成钻杆在平面上做纯滚动运动,如图2所示。

图2 钻杆沿工件内壁运动展开图
由图2易知钻杆的质心速度为:

式中:ω为钻杆的转动角速度,R为钻杆的半径。
钻杆的涡动原理由图3 可知当BTA 钻钻杆在工件内壁纯滚动时,钻杆质心以工件内孔轴线为轴心转动,其转动的角速度为:

式中:ωz为钻杆质心绕工件内孔轴线转动角速度,e为偏心距。偏心距e的表达式为:

式中:D0为内孔直径(工件),Ds为钻杆外径。
由式(1)、(2)以及(3)可得钻杆质心绕工件内孔轴线转动角速度ωz为:

以上分析均未考虑钻削液的楔形作用,当考虑钻削液的楔形作用时,钻杆与工件之间存在滑动或与工件不接触。由式(4)可知钻杆的涡动频率与钻杆的实际转速成正比,然而由于实际运动过程中存在滑动,利用式(4)计算钻杆的涡动频率存在一定误差。
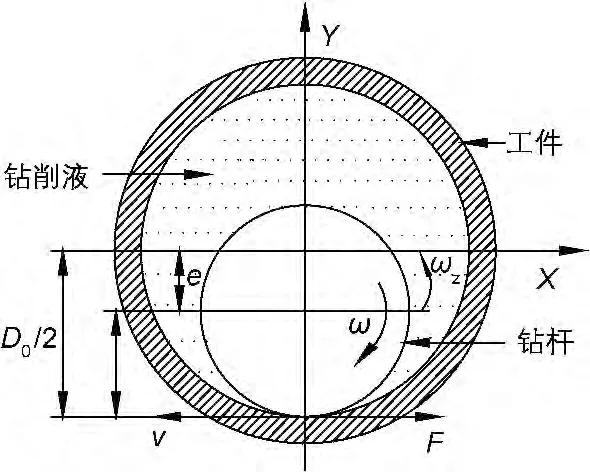
图3 钻杆的涡动原理图
2 BTA 钻杆的典型涡动轨迹
2.1 钻杆的涡动轨迹方程
由BTA 钻杆的涡动分析可知,BTA 钻钻杆的涡动轨迹方程可以用内摆线方程表示。并假设BTA 钻杆与工件内孔的接触为线接触,运动过程中钻杆以及工件无形变发生,钻杆始终与工件内孔接触,则可得钻杆外圆上一点B的涡动轨迹方程为:
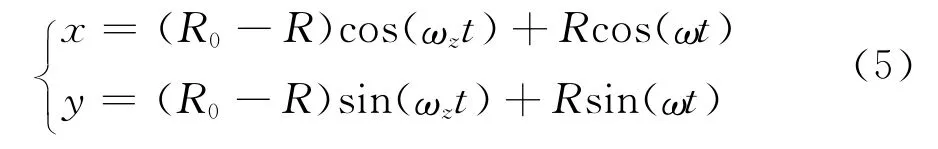
式中:R0为工件内孔半径,x、y分别为钻杆外圆上固定点B的横、纵坐标。
考虑到钻杆与工件内孔间的间隙、涡动的时间、钻杆转速以及涡动频率的变化,可得实际钻杆的涡动轨迹为:
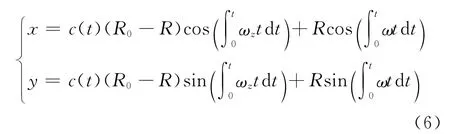
式中:c(t)为钻杆与工件内孔的间隙函数。
在BTA 钻钻削过程中测得钻杆相应的转速、相位、位移等参数就可得到实际的钻杆涡动轨迹。
2.2 BTA 钻钻杆的典型涡动轨迹
由钻杆外圆上一点B的涡动轨迹方程(5)可知,当工件内孔半径、钻杆外径以及钻杆转速确定时,不同的涡动频率,钻杆将有不同的涡动轨迹。利用Matlab软件Plot命令对其进行仿真可得下页仿真图4~12。仿真参数为:钻杆半径R=23mm,工件内孔半径R0=25 mm,转速ω=10rad/s。
由图4可知当涡动角频率ωz=0,即不存在涡动时,无论钻杆是否与工件接触,钻杆外圆上固定点B的运动轨迹就是钻杆外圆本身。由图5可知当涡动角频率ωz=5rad/s时钻杆外圆上固定点B的轨迹为2个相切的内圆,整个运动过程中只与内孔中的一点接触。由图6 可知当涡动角频率ωz=10rad/s时,钻杆外圆上固定点B与工件内孔始终接触,固定点B的运动轨迹为工件内孔,此时工件处于稳定涡动状态。由15~16页图7~11可知当涡动角频率为钻杆转速的整数倍时,钻杆外圆上固定点B的轨迹与工件内孔的接触次数随着涡动角频率的增加而增加,即钻杆的涡动频率越高钻杆的涡动也就越剧烈。
由式(4)可知,当钻杆半径R=23mm,工件内孔半径R0=25mm,转速ω=10rad/s时,钻杆的涡动角频率ωz=115rad/s,因此在纯滚动的假设条件下,钻杆上固定点的运动轨迹如16页图12所示。由图12可知,钻杆固定点的速度是随着时间周期性变化的,由于周期性变化而产生的交变应力将引起钻杆的疲劳损坏。

图4 ωz=0时固定点B 的运动轨迹
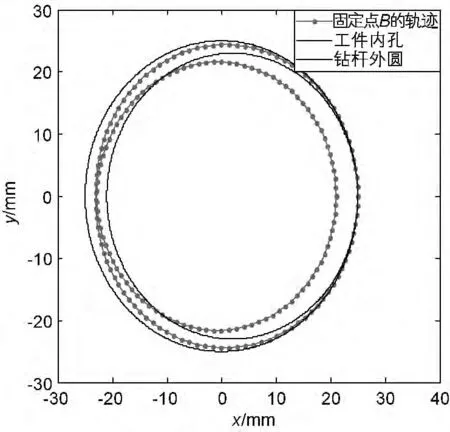
图5 ωz=5rad/s时固定点B 的运动轨迹
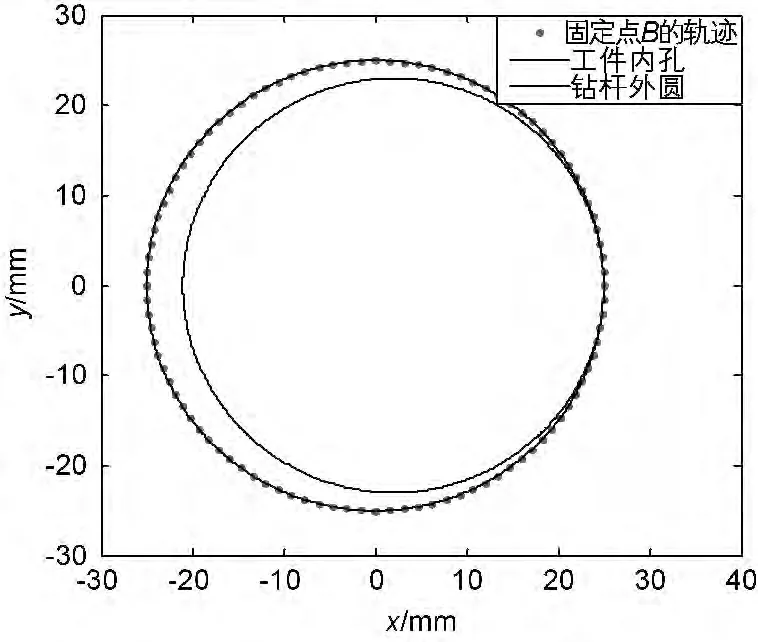
图6 ωz=10rad/s时固定点B 的运动轨迹
3 结论
本文对BTA 钻钻杆的涡动进行了分析,在忽略钻削钻杆与工件相对滑动的前提下,解出了BTA 钻钻杆的涡动频率,建立了BTA 钻钻杆的涡动轨迹方程,基于以上方程对BTA 钻的典型涡动轨迹,利用Matlab软件进行了仿真分析,并得出以下结论:

图7 ωz=30rad/s时固定点B 的运动轨迹

图8 ωz=40rad/s时固定点B 的运动轨迹

图9 ωz=50rad/s时固定点B 的运动轨迹
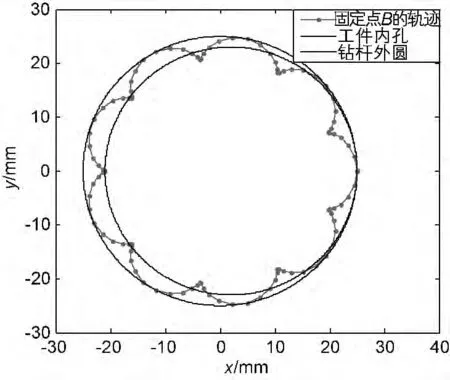
图10 ωz=100rad/s时固定点B 的运动轨迹
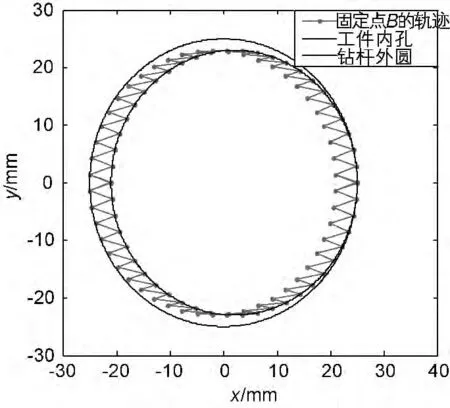
图11 ωz=500rad/s时固定点B 的运动轨迹

图12 ωz=115rad/s时固定点B 的运动轨迹
1)钻杆在发生涡动时,钻杆某一点的速度是随着时间变化的,且钻杆的涡动频率越高钻杆速度变化越大,且周期越短,钻杆由于周期性变化而产生的交变应力将引起钻杆的疲劳损坏。
2)钻杆的涡动频率与钻杆的转动角速度成正比,与间隙C成反比。因此当加工工件孔的直径较大时,间隙较大,涡动频率较小,可以选择较大的转速;当加工工件孔的直径较小时,间隙较小,此时应选择较小的转速减小涡动频率,从而提高钻杆的稳定性。
[1]王峻.现代深孔加工技术[M].哈尔滨:哈尔滨工业大学出版社,2005.
[2]王世清.深孔加工技术[M].西安:西北工业大学出版社,2003.
