瞄准中考,未雨绸缪
——非毕业年级也要及时做好知识点的专题小结
2018-11-01山东省东营市广饶滨海学校张玫瑰
山东省东营市广饶滨海学校 张玫瑰
一、汇总基本图,成龙配套成一体,以便学生做题时独具慧眼,做出精准判断
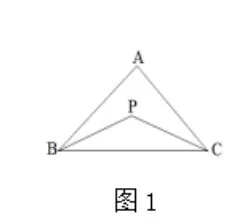
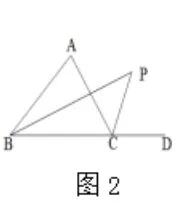
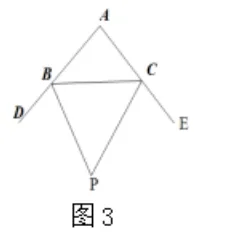
在学习三角形角平分线的内容时我把三角形两个内角的平分线形成的夹角与第三个内角的关系,两个外角平分线形成的夹角与第三个内角的关系,还有一个内角一个外角的平分线形成的夹角和第三个内角的关系,放在一起做了一个专题课。课堂上和同学们一起详细
学生在填空和选择题中若是遇到此类问题,“拿来主义”,直接搬出结果运用即可,不仅节省了做题的时间,准确性也得到了保障,还为综合题的分析降低了难度。
二、把图形做形象的比喻,让学生铭记在心
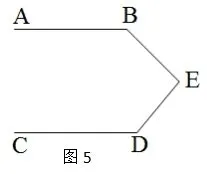
在学习平行线的时候,我和学生给下面的两个基本图分别命名为M型和子弹型,通过从E点添加平行线得出图4的结论是∠E=∠B+∠D,图5的结论是∠B+∠E+∠D=360°,通过对这两个模型的探讨,学生对如下问题的解决可操纵自如了。
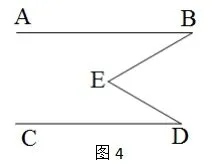
三、引导学生对现实问题抽象简化和量化,构建数学模型
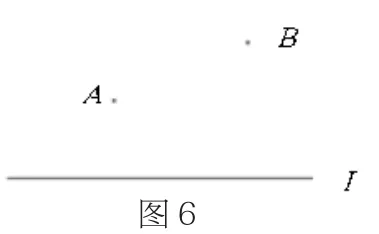
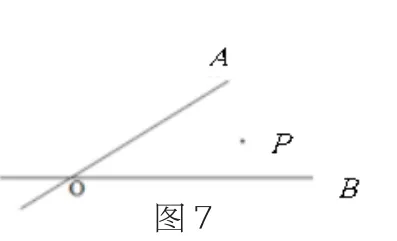
我们在学习最短路径问题时,给学生建立了两种情况的模型,分别命名为“饮马问题之一”“饮马问题之二”。问题一是两点在一条直线同侧时的情形:如图6,牧马人从A地出发,到一条笔直的河边l饮马,然后到B地。牧马人到河边的什么地方饮马,可使所走的路径最短?问题二是在相交直线形成角内部有一点的情形:如图7,牧马人从P地出发,到草地OA某处喂马,再到河边OB某处饮马,然后回到P处,请画出最短路径。
在这个专题学习的基础上,学生在后面的学习中初次遇到此类问题的应用,虽然做起来不是得心应手,但经过一点拨,很快就能成功抽象出数学模型,确定是问题一、二的哪种类型。
四、对于函数中的自变量取值范围的确定,进行群分类聚特别探讨
在进行这个专题的备课时分了五种类型举例探讨:
(1)整式型:取值范围全体实数。例1:求函数y=2x-8的自变量取值范围。分析:因为无论x取任意实数,2x-8都有意义,所以x的取值范围是全体实数。
(2)分式型:取值范围是使分母不为零的实数。
(3)偶次根式型:取值范围是使被开方式非负的实数。
(4)复合型:综合取值范围。
(5)实际问题型:考虑两个因素:自变量自身的意义;问题中的限制条件,引导学生确定自变量取值范围时,首先应找准函数所属类型,然后根据不同类型运用相应的方法来加以确定,这样能快速、准确地解决问题,从而收到事半功倍的效果。
五、一元二次方程求参数专题:
引导学生先搭建全方位框架,再精雕细琢,以防掉进“陷阱”里。也就是说对于一元二次方程求参数的问题先高屋建瓴地根据明显的条件和隐含的条件列出提纲,再根据条件列出具体的关系式。常用到的条件有:(1)二次项系数是否为0;(2)根的判别式;(3)根与系数的关系;(4)题目中的其他条件。
专题小结让我在教学中感受到了雨后的彩虹,收获的喜悦增添了我的研究兴趣,反思总结成为工作的常态,在教与学的过程中,我与学生齐驱并进,在“百般红紫斗芳菲”中诗意的栖息在校园,享受自己的教学工作。
