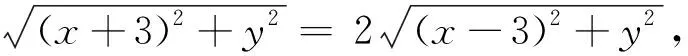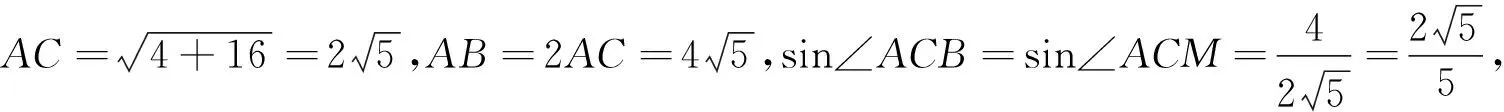用坐标法研究一类不定三角形问题

广东省惠州市实验中学 (516008)

肖志向

近几年高考试题和模拟试题中频繁出现一类解三角形问题——已知三角形的一边及对角求三角形有关元素(边长、周长及面积等)的最值.这类问题主要考查正(余)弦定理、三角恒等变换及基本不等式等相关知识和学生的分析思维、运算能力.

众所周知，只知道三角形一边及对角，这样的三角形是不定三角形.这类解三角形最值问题都是以不定三角形为基础，结合能力考查要求来命制的，不定三角形是根本.对此，笔者用坐标法研究了这类不定三角形并探究了相关元素的最值.

一、问题

已知AB=2m，C=θ(0<θ<π)，试确定点C的轨迹.

一)用坐标法探究不定三角形动点的轨迹，挖掘其几何背景

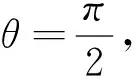
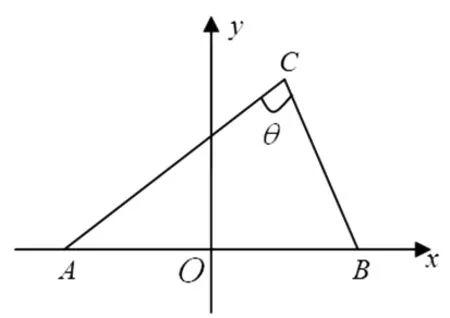
图1

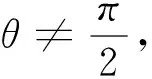
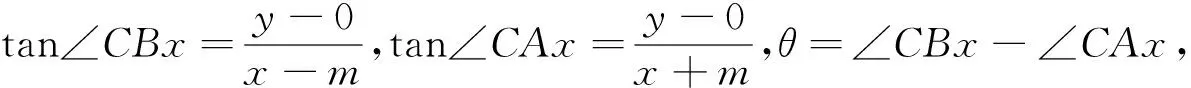
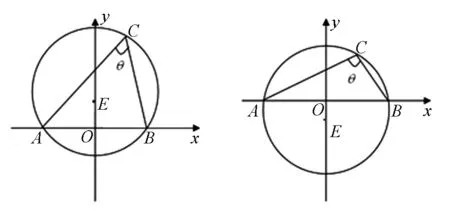
图2 图3

综合以上可知：平面内与两定点所成的角为定值的点的轨迹是过这三个点的圆(即外接圆)上定弦所对应的一段弧.这类不定三角形可看成为某一定圆(其直径等于该边与对角正弦的比值)内接三角形，已知边是圆内一条定弦，动点为该定弦所对弧上一动点.

二)探究这类不定三角形相关元素的最值结论

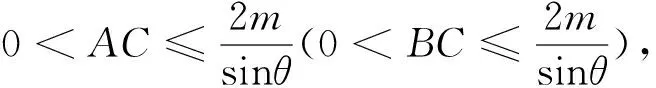
二、用坐标法解这类不定三角形为题根的习题

一)直接利用这类不定三角形的最值结论，解决三角形的有关最值问题

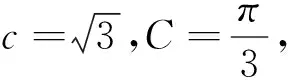
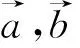
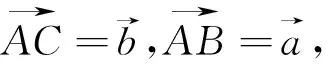
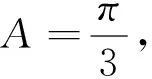
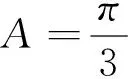
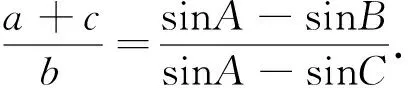
(1)求角C；

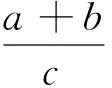
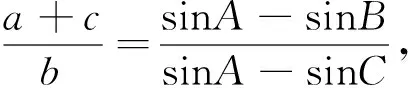
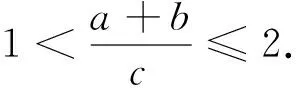
二)用坐标法解答不定三角形为基础的变式题，求平面图形相关最值问题

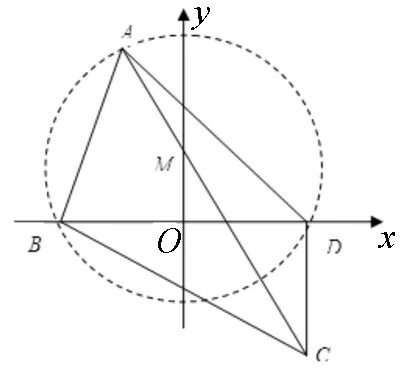
图4

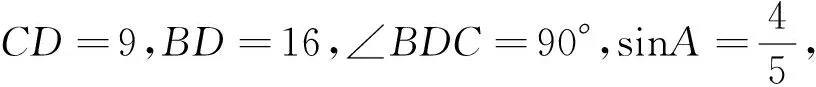
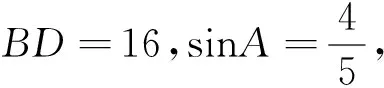
成立当且仅当点A在圆M优弧上且AC经过圆心M，故对角线AC的最大值为27.

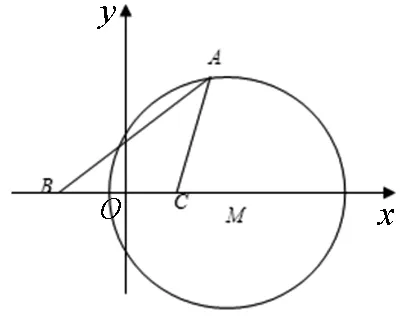
图5

例6 已知在ΔABC中，BC=6，AB=2AC，则ΔABC面积最大时，sinA的值为 .