巧用构造法妙解高考填空题

南京师范大学教师教育学院 (210097)

林 娴

填空题是高考数学题中重要的一部分,有的题目若按照一般的解题思路常常难以得到解决,甚至无从下手,有时利用“构造”这个巧妙的方法可能会有新的发现.笔者对一部分时常遇到的以及能够运用构造法巧妙解决的高考填空题进行反思与归纳,发现在一些求取值范围、求最值以及向量等问题中能够运用构造法巧妙解题.通过这些反思归纳,希望在高考填空题中运用这些方法能够让解题思路更加清晰.

常用的构造法有构造函数、构造几何图形、构造公式与构造方程等.以下结合一些典型的例子,来谈谈构造法在一些题目中的具体运用.

一、巧构函数，得心应手

许多高考题中渗透着函数的思想,可通过寻找同构式与联想求导法则等方法来构造特殊的函数,从而将复杂的数学问题转化成函数的问题,再利用函数的一些相关性质来解决.

1.寻找同构式

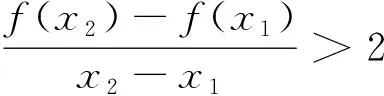
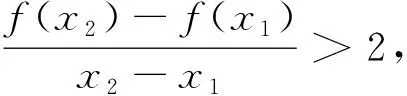
2.联想求导法则

例2 已知f(x)是定义在R上的奇函数,且f(1)=0,xf′(x)-f(x)>0(x>0),不等式f(x)>0的解集为 .

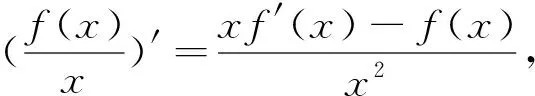
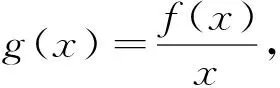
二、巧构图形 数形结合

构造几何图形也是构造法中常用的方法之一.代数问题一般较抽象,难以入手,这时可利用数形结合的方法,根据题干条件构造出一些几何图形等来解决代数的问题.

1.构造直角三角形

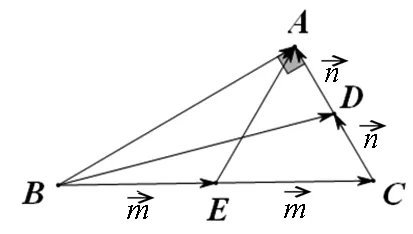
图1

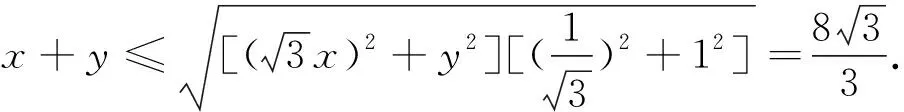
2.构造圆

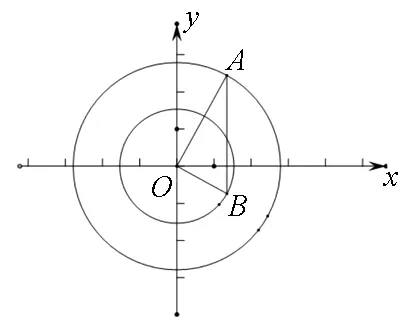
图2

分析:此题按常规做法可通过求导计算,求得最小值,从而算出a的值,但是这样计算太过于繁琐,可通过构造圆的方法来巧妙解题.分母有理化得f(x)=

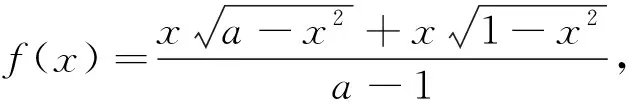
3.构造椭圆

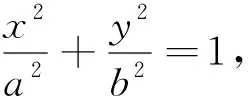
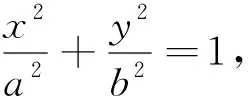
三、巧构公式 左右逢源

有时题中的代数式可以通过配方、拼凑等方法,转化成点与点、点与线或线与线的距离公式,从而将代数问题转化为几何问题,解题也就更加轻松快捷.

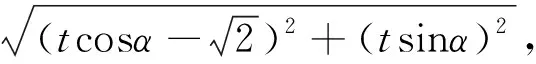
四、巧构方程 意外收获

求解一些不等式问题,有时可能不知如何利用不等式的相关性质求解最值.这时构造方程就是一条新的路径,构造一元二次方程,再利用一元二次方程根的判别式即可求出.

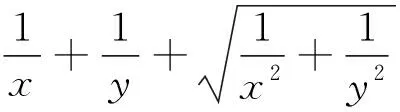
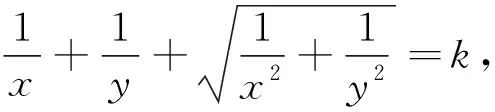
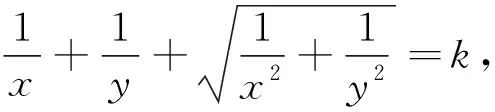
五、结语

由上可见,解决高考数学填空题时可以利用构造法达到巧妙解题的效果,从而将一些“无从下手”的题转化成熟悉的问题,从而使得解题更加得心应手.但是数学解题并不总是有固定的模式,有时构造出的“成品”的“优”与“劣”会影响解题的结果,故应根据实际情形进行变通,找到更简便、更快捷的解题方法.