以形助数——巧解恒成立问题

江苏省海门市海门中学 (226100)

樊陈卫

恒成立问题是各类数学考试中的常见试题，其解法通常是通过分离参数，再转化为某个函数的最值与含另一个代数不等式解决问题.但当此类问题作为试卷的压轴试题时，就会发现用这个思路来解题有时会碰壁，这时就需要解题者准确把握题目中的条件特征，合理挖掘利用其关键信息，如能构作函数的图像，题目往往能顺利解决.这里通过几个例题加以说明.

一、构造两点距离

例1 已知不等式(m-n)2+(m-lnn+λ)2≥2对任意m∈R,n∈(0,+∞)恒成立，则实数λ的取值范围为 .

分析:本题若按常规思路考虑分类参数法，则

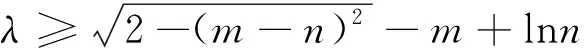
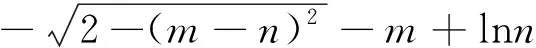
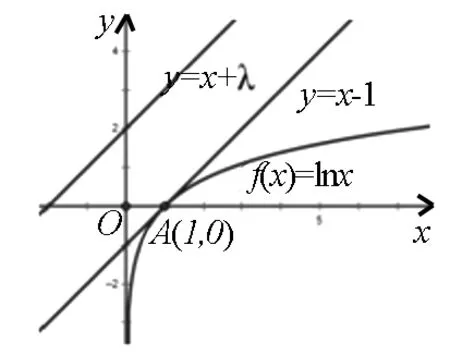
图1

二、变换构造图像

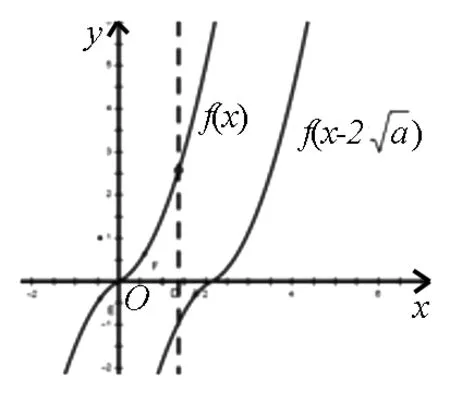
图2

解:由已知f(x)=

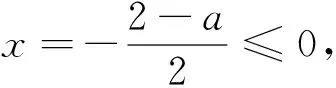
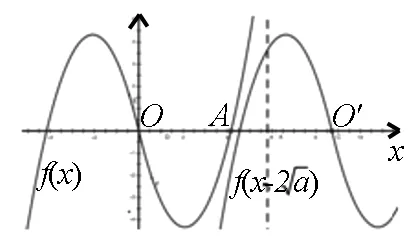
图3

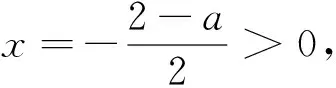
三．巧用图像“全等”

四、把握图像特征

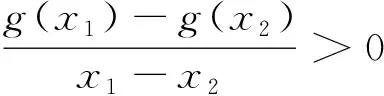
图4

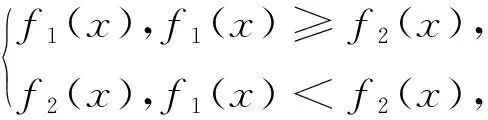
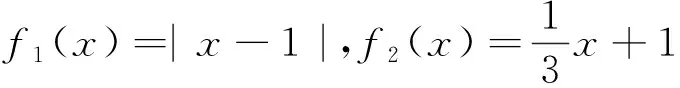
分离参数法是解决恒成立问题的通性通法，但如果把它当做恒成立问题的唯一方法，有时会陷入被动局面.打仗时只有善于发现对方的弱点，才能攻其不备，取得胜利，解题犹如打仗，善于把握题目的关键特征，灵活应用各种思想方法，才能做到游刃有余.