大气闪烁对纠缠相干态量子干涉雷达影响机理∗

任益充 王书 饶瑞中 苗锡奎

1)(中国科学院安徽光学精密机械研究所,中国科学院大气光学重点实验室,合肥 230031)

2)(中国科学技术大学研究生院科学岛分院,合肥 230026)

3)(光电对抗测试评估技术重点实验室,洛阳 471003)

(2017年11月8日收到;2018年4月22日收到修改稿)

介绍了量子干涉雷达物理模型及其探测原理,并采用耗散-涨落通道处理量子光场在湍流大气中的传输,从经典湍流统计理论推导得到大气透射率的概率密度分布函数P(T),以此为基础系统分析了大气闪烁效应对纠缠相干态量子干涉雷达的影响机理,深入讨论了平均大气透射率、闪烁指数等大气参数对系统目标探测性能的影响.研究发现:低损耗情况下系统灵敏度及分辨率性能随闪烁指数的增加而降低;高损耗情况下大气闪烁则能显著提高系统灵敏度和分辨率性能,且界定高低损耗的透射率临界点随脉冲光子数增加而增加,故大气闪烁能够在一定程度上克服大气损耗造成的不良影响.

1 引 言

雷达是发明于20世纪用以远程目标探测及测距的传感设备,在火控、防空、预警等军事国防领域和航空、气象等民生领域均发挥着重要作用.经典雷达技术历经70多年的发展,其理论、体制、技术实现及应用均取得了很大进展,从单纯利用回波信号的强度信息到对信号频率、相位信息的综合利用,有效提升了雷达的抗干扰、抗杂波能力;电子技术的快速发展及隐身技术的出现,对现有雷达体系提出了严峻挑战.经典雷达受限于电磁理论的桎梏,很难在提高灵敏度及分辨率、抗电磁干扰、安全成像等方面有所突破,难以满足日益苛刻的军事和国防需求[1].

为应对电子干扰技术和隐身战机的挑战,突破经典雷达在分辨率、灵敏度、抗干扰方面的瓶颈,量子雷达将量子光学及量子信息技术引入遥感探测领域[2],利用量子理论对接收机噪声、散粒噪声等给予全新解释并从调制载体、测量检测等方面入手全面提升雷达的综合性能[3].量子雷达或通过发射相干态、压缩态、纠缠态等量子信号对目标区域进行照射,并对回波信号采用相干探测、符合测量等量子手段进行检测,或在雷达接收端采用量子增强技术对回波信号进行无噪声放大以提升性能.与经典雷达相比,采用量子信号和光量子测量技术的量子雷达拥有超灵敏度、超分辨率、抗电磁干扰、散射截面和功耗体积小等诸多优势[4−6].

鉴于量子雷达的诸多优势,未来其在军事国防、工程测绘、空间探测、空天对抗等领域有着重要应用,如量子雷达凭借超灵敏度、超分辨率等特点能够探测隐身目标、雷达安全成像,亦可用于探测近地空间中的陨石和卫星碎片以及对于近地小行星的跟踪监测等.此外,量子雷达研发需要雷达波段的激光光源及相应频段的光学器件及探测器等,这些技术的突破也将进一步促进量子通信、量子传输、量子计算等量子信息技术的飞速进展.

量子雷达的理论研究和原理论证起步较早,Bakut[7]于1966年率先探讨了在雷达系统中使用量子信号的可行性;进入21世纪后,美国防部高级研究计划局(DARPA)先后启动的量子传感(quantum sensor)、量子激光雷达(quantum lidar)、单光子信息(information in a photon)等项目标志着量子雷达研究领域的正式创立;随后军方、企业、高校的研究团队提出了三种主要的量子雷达方案:量子照射、接收端量子增强和干涉式量子雷达,其中量子干涉雷达方案使用量子光场扫描目标区域,并将回波信号与参考信号进行相干测量,通过选取合适的光场及检测方案即可利用光场的纠缠、压缩等量子特性使得雷达的灵敏度和分辨率分别突破散粒噪声极限和衍射极限[8−10].

大气环境对量子光场传输过程中的干扰是量子雷达实用化过程中必须克服的障碍,在对大气层内目标进行探测时,量子雷达所发射的光量子信号被广泛存在于大气中的粉尘、微粒、气溶胶等吸收和散射,使得光子产生损耗.此外由大气温度、风速的随机分布产生10−3—103m尺度的湍涡进一步引起大气折射率的起伏,使光场在传输过程中出现大气闪烁、相位起伏等大气湍流效应,这些效应将致使量子光场在传输过程中发生退相干、退纠缠等现象,进一步导致光场丢失其量子特性蜕化为经典光场,这将严重影响量子雷达的灵敏度、分辨率等性能.

目前学术界对于量子雷达的方案设计及性能进行了较为系统的研究,而对于大气介质对量子雷达的影响机理的研究则较为匮乏,已有研究局限于大气损耗的影响.文献[11]系统研究了大气损耗对相干态量子干涉雷达的影响,指出当探测光与参考光透射率不同时,其灵敏度随平均脉冲光子数的增加先提高后降低,单纯增加发射功率导致灵敏度的迅速下降;调节参考光透射率等于探测光透射率,同时增大发射功率即可完全克服大气损耗造成的灵敏度降低.然而激光在真实的大气环境中传输时,大气闪烁效应将使得探测光光强出现kHz级别的涨落,此时很难保证参考光与探测光透射率的实时匹配,所以有必要深入研究大气闪烁对量子雷达性能的影响.

本文首先讨论纠缠相干态量子干涉雷达的物理模型和探测原理,给出光场在损耗通道中的演化过程并讨论大气透射率对其性能的影响,结合经典湍流统计理论推导大气透射率系数的概率密度分布函数(PDTC函数)P(T),将大气介质视作耗散-涨落通道进行处理,并研究平均有限面积光强闪烁指数等对纠缠相干态量子干涉雷达性能的影响,激光波长、束腰半径、折射率结构常数、传输距离、接收口径等参数通过影响进而间接影响量子雷达的灵敏度与分辨率.本文内容安排如下:第2节给出量子雷达模型并求解出光场在耗散通道中的演化过程,利用宇称算符探测接收到的信号的相位信息,并给出分辨率与灵敏度的表达式;第3节介绍已有的对大气透射率概率密度分布函数的研究,并从经典湍流理论出发推导出相应的大气透射率概率密度分布函数;第4节对量子干涉雷达的灵敏度、分辨率进行绘图研究,并系统探讨各参数对雷达性能的影响;第5节对本文的研究成果和结论进行简单总结.

2 量子干涉雷达目标探测原理

量子干涉雷达向目标区域发射相应的量子光场,将接收到的信号光与参考光进行干涉并选择合适的探测方案进行测量,从而实现超灵敏度、超分辨率的远程目标探测.图1(a)和图1(b)分别是纠缠相干态量子干涉雷达的探测原理和模型示意图.

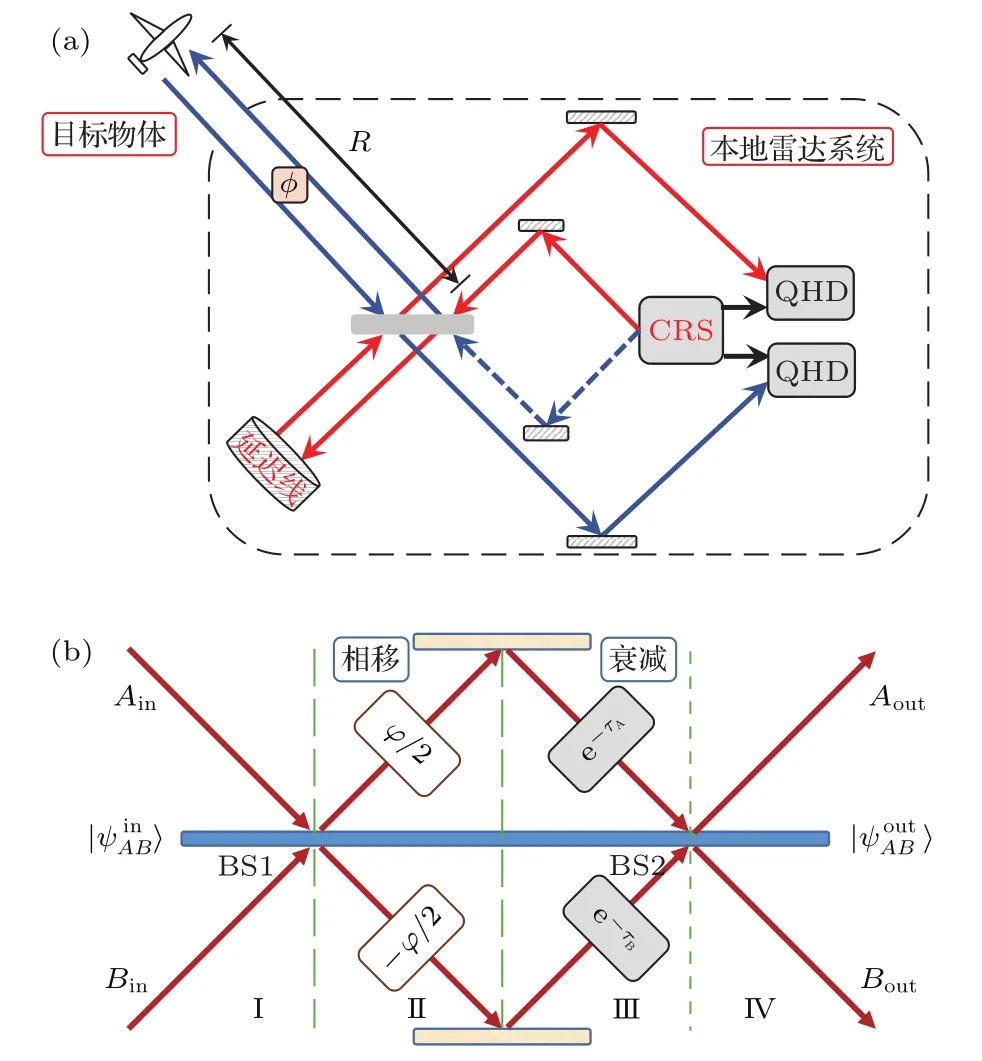
图1 量子干涉雷达探测原理及物理模型 (a)探测原理;(b)物理模型Fig.1.Detection theory and physical model of quantum radar:(a)Detection theory;(b)physical model.

图1中CRS和QHD分别代表激光光源与信号探测系统,奇偶相干态与相干态两路激光信号经分束器产生纠缠相干态,一路留在本地进入光纤延时线(delay line,DL)作为参考光,另一路作为探测光扫描目标区域.由于两束光的光程不同会产生一定的相位差,随后将接收到的探测光与参考光在分束器上重新干涉,并采用量子光学的方法对其进行相干检测即可测得此相位差,从而能够探测到目标的距离信息.量子干涉雷达的核心干涉部件可视作马赫-曾德尔干涉仪(MZI),故可用图1(b)中的MZI模型对量子干涉雷达的目标探测原理进行深入分析.图1(b)中BS1/BS2代表50:50的分束器(beam spilter),从左侧Ain,Bin端分别输入奇偶相干态和相干态,在BS1处干涉产生相干纠缠态,上下两束光的光程不等导致两者间产生大小为φ的相位差.参考光与探测光在传输过程中均存在一定程度的损耗,TA,TB分别代表两路光的透射率;被目标反射回来的探测光与参考光在BS2处再次干涉后,通过对Aout或Bout端的信号进行检测即可测得关于相位φ的信息,进而精确探测到目标的距离信息.

首先考虑如何通过BS1产生纠缠相干态,在Ain,Bin端分别输入奇偶相干态与相干态,即

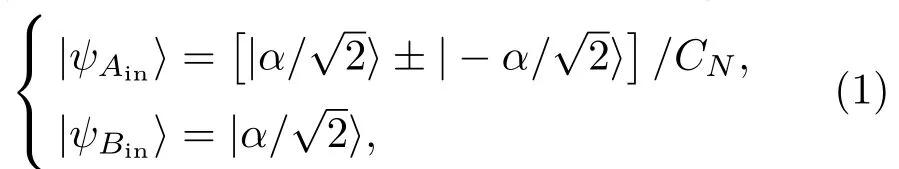
式中CN=2(1± e−|α|2),输入端初态|ψin为

若忽略分束器对透射光和反射光的附加相位差问题,则可用幺正算符Uy(θ)=exp(−iθJy)描述分束器对光场的作用,通常对于50:50分束器θ可取±π/2[12].此外还有另外一种采用谐振腔代替分束器的非线性干涉仪,与线性干涉仪相比,非线性干涉仪的器件复杂但灵敏度更高,非线性干涉仪的部分研究结果可参见文献[13—15].干涉仪Ain,Bin端输入光场经分束器BS1演化为纠缠相干态

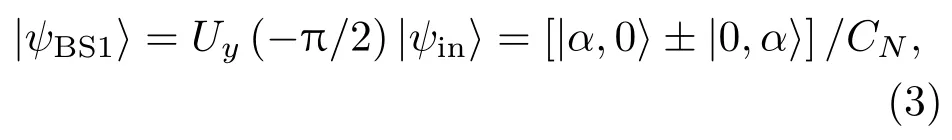
随后探测光与参考光的光程差使得二者出现为φ的相位

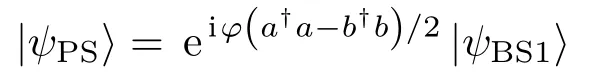
需要指出的是,光场在传输过程中必然要考虑大气损耗的影响,该过程可由如下耗散主方程描述[16,17]

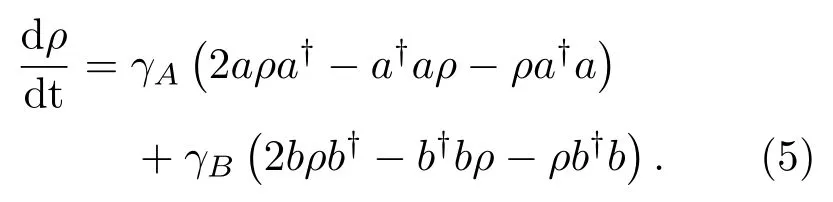
文献[18]给出(5)式Kraus算符解,

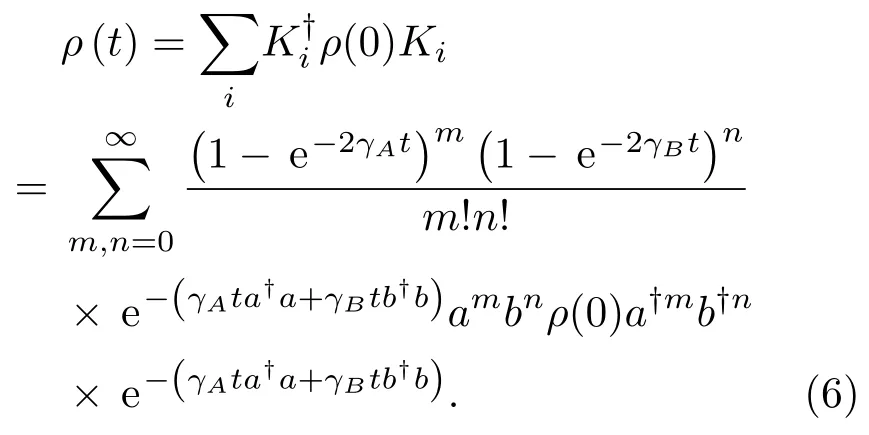
式中TA=e−2γAt,TB=e−2γBt分别代表探测光和参考光的大气透射率,由上述结果可给出经损耗衰减后的密度算符,

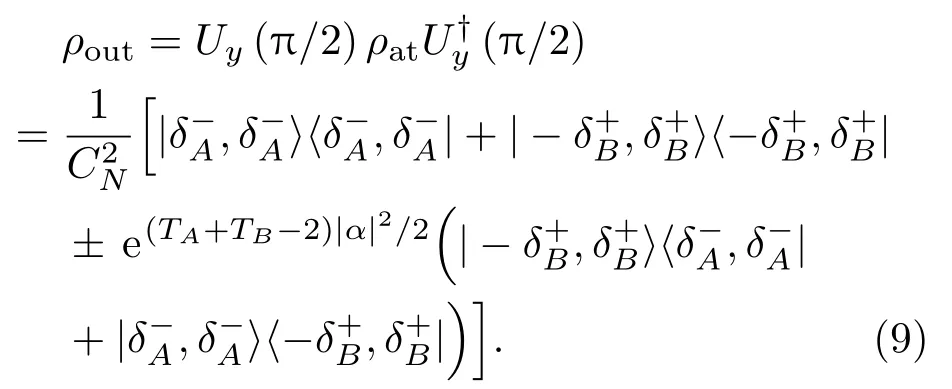
则测量结果为

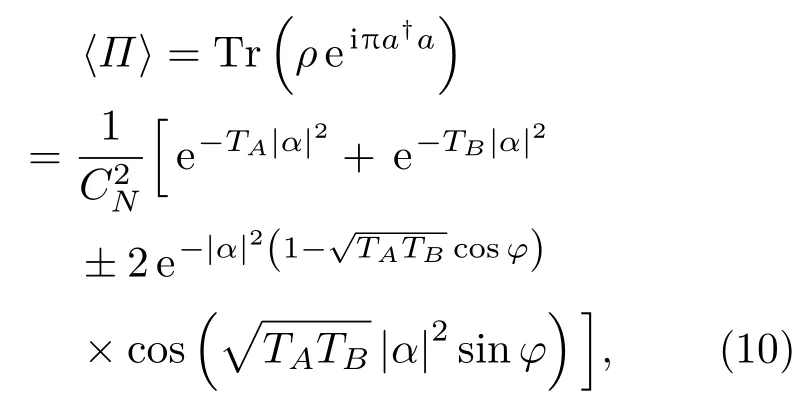
这样即可通过宇称算符间接探测相位φ,从而精确地测得目标的距离信息,其距离分辨率与信号的半高宽有关.量子干涉雷达的灵敏度∆φ代表相位探测的标准差,灵敏度越高∆φ越小,意味着测量越准确误差越小.相位φ是通过间接测得的,因此其标准差的误差传递公式为

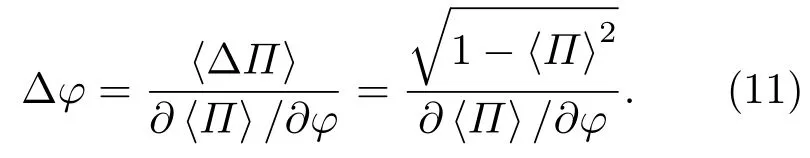
由以上推导过程可知损耗将直接影响量子雷达的分辨率和灵敏度,故探测光、参考光的透射系数TA,TB是耗散通道的关键参数,在以上研究过程中将光场的大气传输视作耗散通道,并将TA,TB均作为常数进行处理.真实的大气环境中,探测光在大气传输过程中不可避免地受到大气湍流的影响,大气闪烁引起的光强起伏将导致透射率的随机起伏,故须推导大气透射率概率密度分布函数(probability distribution of transmission cofficient,PDTC)P(T)以研究大气闪烁对量子干涉雷达的影响机理.探测光的PDTC函数P(T)不仅受大气参数的影响,同时也受激光波长、束腰半径、接收口径、传输距离等其他参数的影响,大气透射率的具体分布函数是研究的关键点之一.

3 大气透射率概率密度分布函数

如图2所示,当激光在湍流大气中传输时,大气湍流造成的折射率起伏使得光束的波前相位出现随机起伏,进而导致接收端光强的起伏,即大气闪烁效应.20世纪50年代,Tatarskii[19]和Fante[20,21]采用Rytov近似法并引入现代湍流统计理论,给出弱湍流区内平面波和球面波的Rytov解,成为处理若湍流条件下光传播的经典理论.Semenov和Vogel[22]以及Vasylyev等[23]基于光束扩展和漂移给出了PDTC分布,并将其应用于空间量子通信研究.为进一步研究大气闪烁对量子干涉雷达的影响,本节将从经典湍流统计出发推导PDTC函数的具体形式.

图2 大气闪烁原理示意图Fig.2.Sketch-map of atmospheric scintillation.

为进一步研究大气闪烁对量子干涉雷达的影响,有必要从经典湍流统计出发,重新推导PDTC函数.本节将从大气闪烁效应本身出发,给出PDTC函数的另一种形式.首先定义大气透射率为接收功率与总功率之比

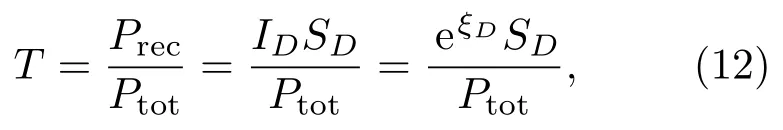
其中Prec,Ptot分别代表接收功率与光束的发射总功率;ID,SD则代表接收光强及接收面积,ξD=lnID代表口径D内接收的对数光强.理论和实验都证明弱起伏条件下光强起伏符合对数正态分布,即ξD服从如下正态分布:

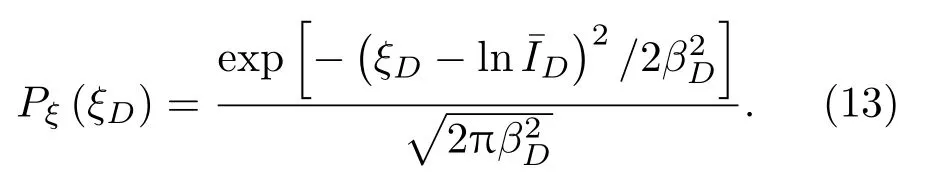
利用(12)式及(13)式即可得到大气透射率T的概率密度分布函数

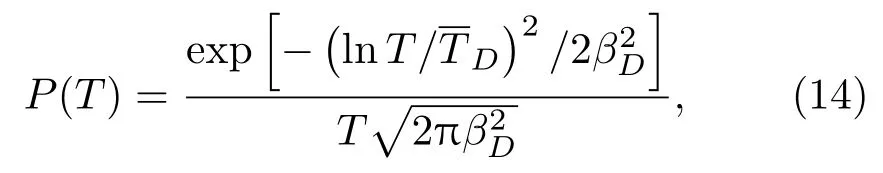
根据经典湍流理论可由Rytov近似求得对数振幅起伏χ的二维谱密度,进一步求其相关函数和结构函数,并得到相应的弱起伏条件下闪烁指数与之间存在关系==exp−1≈在对具体的传播问题求解时还需要考虑传播条件,量子干涉雷达探测距离L约为104—106m,目前所使用的红外激光器波长λ约为10−6m级别,湍流的内尺度l0约为10−3m,外尺度L0约为100—102m,基于以上估值分析,(衍射区),此条件下应采用Kolmogorov湍流谱[24],对应的闪烁指数为

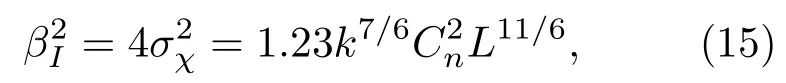
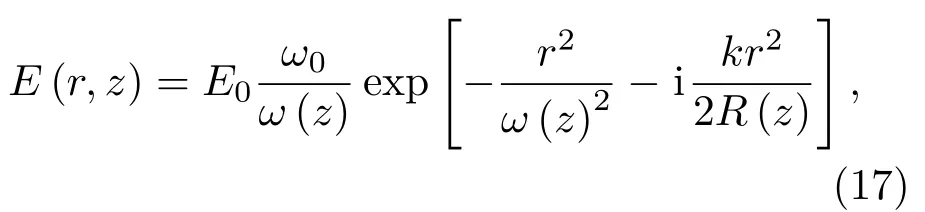
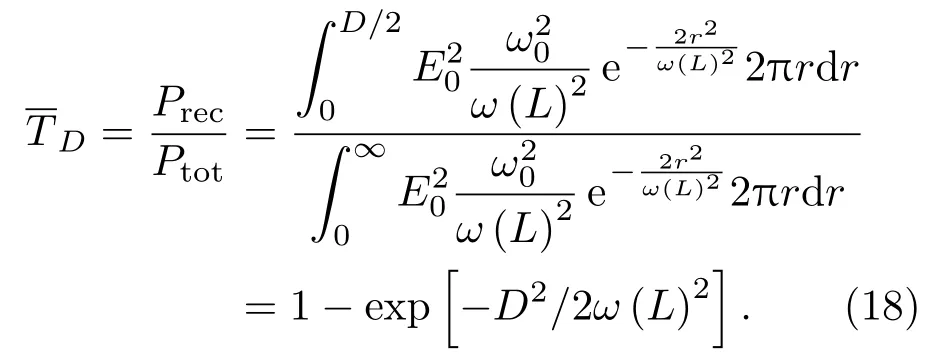
由此可见,PDTC函数主要由λ,ω0,L,D等参数决定,其中λ,L,决定大气透射率的起伏情况即闪烁指数而ω0,λ,L,D决定大气透射率的平均值

4 大气闪烁对量子干涉雷达的影响

通过对大气闪烁效应的分析,推导得到大气透射率T的概率密度分布函数P(T),本节分析大气损耗对纠缠相干态的量子干涉雷达影响,并与相干态量子雷达的情况进行比较,随后进一步研究大气闪烁效应对其性能的影响,从入手,逐渐深入并单独分析λ,ω0,L,D等部分参数的影响.

首先考虑损耗对量子干涉雷达分辨率和灵敏度的影响.由(10)式可看出

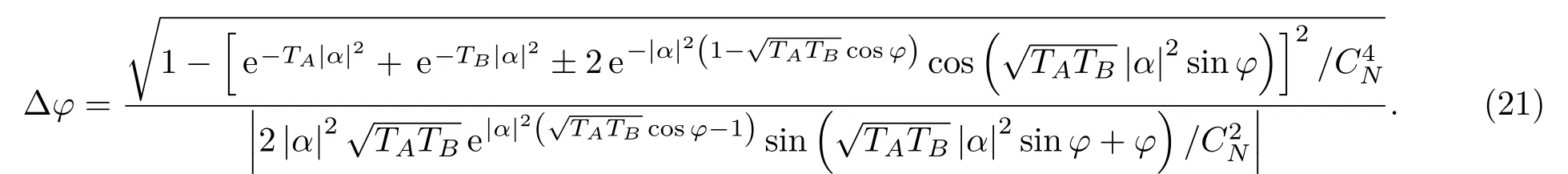
将灵敏度∆φ进行绘图,如图3所示.图3(a)为无损耗情况下系统灵敏度∆φ随相位φ的演化,从图3(a)和图3(b)中可知∆φ的最小值出现在φ=0点且随着N的增大而减小,将TA=TB=1,φ =0代入(21)式可得∆φ =∆φ =1/N且∆φ<1/N,这说明无损耗情况下纠缠相干态量子干涉雷达的灵敏度可达到1/N的海森伯极限;图3(c)显示当存在损耗时,∆φ的最小值∆φmin不再出现在φ=0处,结合图3(b)可知∆φmin随平均脉冲光子数N的增加出现先减小后增大的趋势,这说明增大N可能导致∆φmin增大,即灵敏度降低,故单纯增加发射功率无法克服损耗造成的灵敏度下降;综合比较图3(b)和图3(d)可发现,低损耗情况下系统的灵敏度在较大的功率范围内随平均脉冲光子数的提高而提高,而高损耗情况下系统灵敏度则随着平均脉冲光子数的上升出现先提高、后迅速降低的情况.

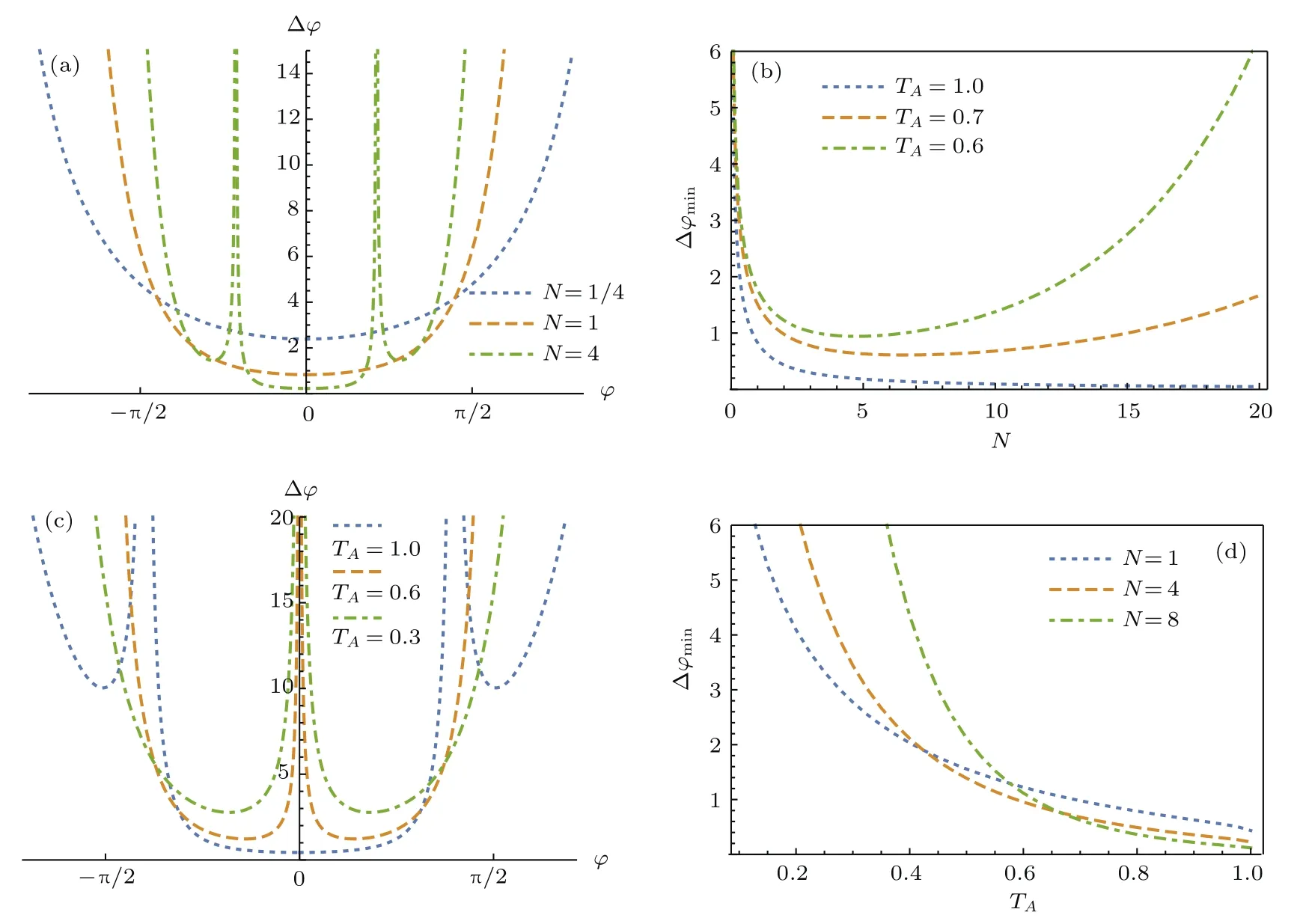
图3 大气损耗及平均脉冲光子数对探测灵敏度的影响 (a)TA=1,TB=1;(b)TB=1;(c)N=2,TB=1;(d)TB=1Fig.3.Influence of atmospheric loss and phonon number on sensitivity of detection:(a)TA=1,TB=1;(b)TB=1;(c)N=2,TB=1;(d)TB=1.

针对大气损耗带来的不良影响,文献[11]指出通过调节参考光的透射率等于探测光透射率,即TA=TB,即可使相干态量子干涉雷达的灵敏度随N的增加而单调递减,同时增强发射功率即可完全克服大气损耗的不良影响.与相干态量子雷达不同,纠缠相干态量子雷达对大气损耗更为敏感,无法通过调节参考光的透射率克服大气损耗的不良影响.造成这种现象的根本原因在于相干态是最接近经典的量子态,其在耗散通道中的演化仍保持相干态,而纠缠相干态则为非经典光场,在耗散通道中的演化逐渐丢失其纠缠、相干等量子特性蜕化为混态,因此无法完全克服大气损耗对纠缠相干态量子干涉雷达灵敏度的影响.综上,纠缠相干态量子雷达的灵敏度在低损耗情况下优于相干态,但在高损耗环境中相干态量子干涉雷达则通过调节参考光的透射率达到更高灵敏度.进一步考察大气闪烁对量子干涉雷达性能的影响,由于λ,ω0,L,D等参数决定平均透射率和闪烁指数的值进而影响PDTC函数P(T),故本文以为主要参数讨论大气闪烁的影响.

首先考虑大气闪烁对灵敏度的影响,在耗散-涨落通道中灵敏度∆的表达式应为

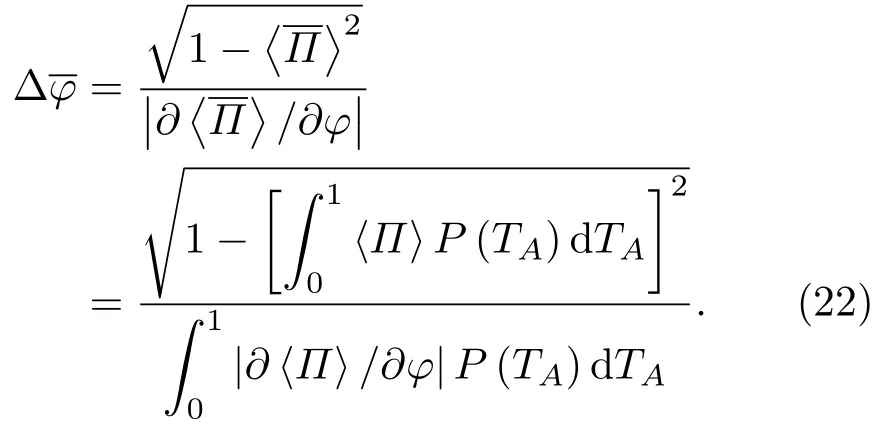
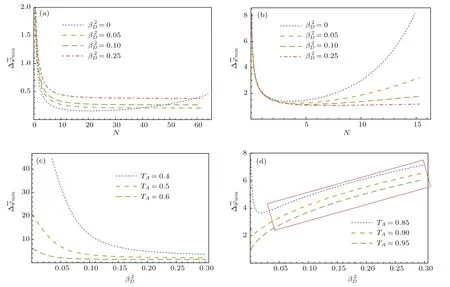
图4 闪烁指数及平均透射率对最佳灵敏度∆的影响(a)=0.5,TB=1;(b)TB=1,N=16;(c)=0.9,TB=1;(d)TB=1,N=16Fig.4.Influence of scintillation indexand mean transmittanceon optimal sensitivity∆:(a)=0.5,TB=1;(b)TB=1,N=16;(c)=0.9,TB=1;(d)TB=1,N=16.

系统灵敏度∆φ代表相位φ的测量标准差,图4(a)和图4(c)为不同损耗和闪烁情况下,系统最佳灵敏度∆随平均脉冲光子数N的变化;图4(b)和图4(d)则为∆随闪烁指数的变化趋势;图4(a)和图4(b)表明较小时∆随的增加而单调递减;图4(c)和图4(d)则显示较大时∆先随闪烁指数增加而缓慢增加(见图4(d)中红色线框内部分).综上,若不考虑图4(d)中红框前面极小的特殊情况,则低损耗情况下闪烁指数的增加将导致系统灵敏度的下降,高损情况下,闪烁指数的增加能显著提高系统灵敏度.

为进一步研究闪烁指数对灵敏度影响的临界透射率,将系统在不同闪烁指数下的灵敏度之差∆|=0.3−∆|=0.1与平均透射率的关系绘图,如图5所示.

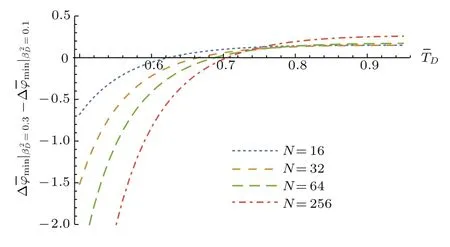
图5 ∆|=0.3−∆|=0.1随平均透射率变化的示意图Fig.5.Schematicdiagramof∆|−∆|vs.mean transmittance

为进一步分析大气闪烁对纠缠相干态量子干涉雷达分辨率的影响,将不同损耗和起伏情况下的信号及其半高宽绘图,如图6所示.

为研究闪烁指数对分辨率影响的临界透射率,将系统在闪烁指数=0.3及无闪烁情况下的脉冲信号的半高宽之差与平均透射率的关系绘图,如图7所示.

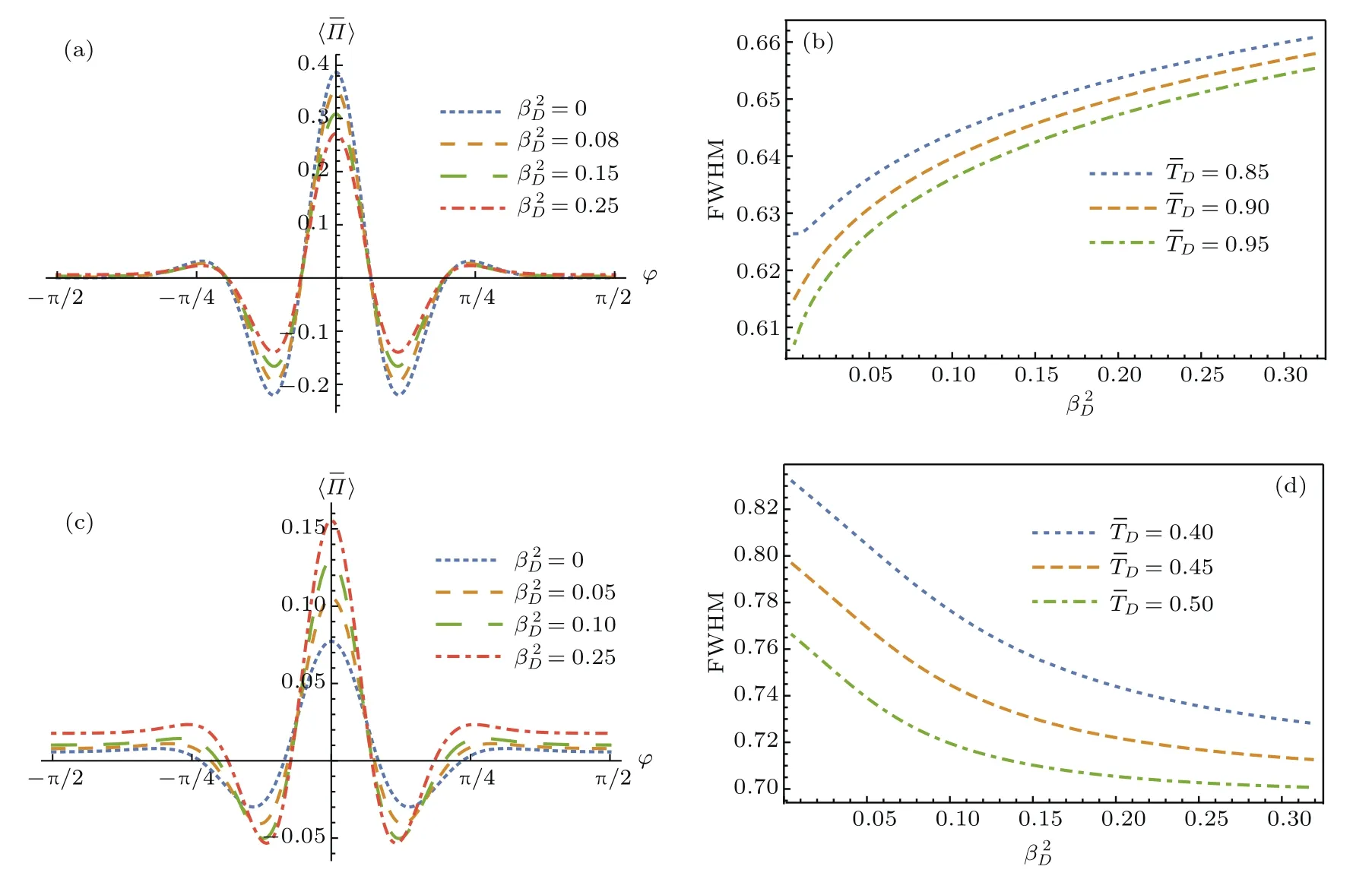
图6 闪烁指数对及其半高宽的影响 (a)=0.8,TB=1,N=9;(b)N=4,TB=1;(c)=0.5,TB=1,N=9;(d)N=4,TB=1Fig.6. Influence of scintillation indexonand FWHM:(a)=0.8,TB=1,N=9;(b)N=4,TB=1;(c)=0.5,TB=1,N=9;(d)N=4,TB=1.

图7 FHWM=0.3−FHWM=0随平均透射率变化示意图Fig.7.The schematic diagram of FHWM−FHWMvs.mean transmittance

研究表明:高损耗情况下系统的灵敏度及分辨率均随闪烁指数的增加而提高,低损耗情况下则相反,灵敏度及分辨率随闪烁指数的增加而下降.一般而言,闪烁指数的增加意味着大气透射率起伏涨落的加剧,涨落会导致误差增大以及系统灵敏度和分辨率的下降.然而研究表明仅损耗较小时情况符合一般结论,损耗较高时情况则与一般结论相悖.进一步分析可知,耗散对量子光场的影响可分为能量损耗与退相干两类,如(4)式中与(8)式中ρat分别为耗散前后的量子态和密度算符,对比二者可知:

1)能量损耗,体现在振幅的衰减,如由

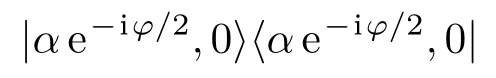
变为

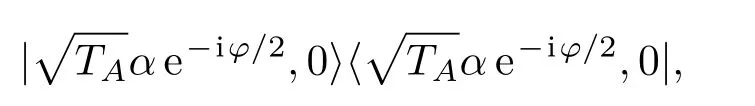
这代表单纯损耗作用引起的振幅衰减;

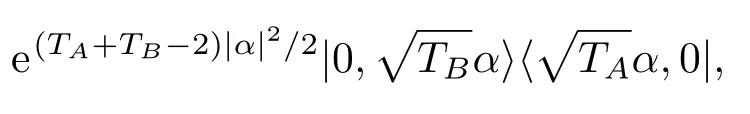
该项前面系数由1衰减到e(TA+TB−2)|α|2/2,这种衰减仅发生在密度算符的非对角项中,代表耗散引起的退相干导致系统逐渐丢失叠加、纠缠等量子特性.

大气闪烁对量子系统的单纯损耗和退相干影响程度的不同是导致灵敏度分辨率随闪烁指数变化规律的根本原因:低损耗情况下,退相干对量子雷达系统的影响较小,此时透射率的涨落将导致灵敏度和分辨率的下降;高损耗情况下量子雷达则受退相干影响为主,受单纯损耗影响相对较小,系统灵敏度的下降主要是由于系统退相干丢失其量子特性引起的,已有研究表明耗散-涨落通道比单纯的耗散通道更有助于保持系统的非经典特性[23],故此时闪烁指数的增加反而能够抑制退相干,保持量子光场的非经典特性,有助于提高其灵敏度和分辨率性能;由(8)式中exp{[(TA+TB)/2−1]|α|2}可知,退相干不仅与透射率TA,TB有关,还与平均脉冲光子数N=|α|2有关,显然N较大时以退相干影响为主,此时由于涨落有助于保持系统量子特性,致使灵敏度和分辨率随闪烁指数增加而提高,这正是图5与图7中透射率的临界点均随N增大而增大的原因.

综上所述,纠缠相干态量子干涉雷达在工作过程中可根据灵敏度、分辨率等需求,适当选择波长、束腰、发射功率、接收口径,进而间接调节N等参数,从而获得较高的分辨率和灵敏度性能.其他参数λ,ω0,L,D等对分辨率和灵敏度的影响主要通过(其对,的影响实现,而(λ,ω0,L,D),λ,L,D的表达式已由(16)式与(17)式给出,这里不再逐项赘述λ,ω0,L,D等参数对纠缠相干态量子干涉雷达的影响.

5 总 结

本文首先介绍了量子干涉雷达的探测原理、发展历程,总结了目前量子雷达大气环境影响机理研究的不足之处;进一步基于马赫-曾德尔干涉仪模型,详细分析了纠缠相干态量子雷达的探测原理,并采用耗散-涨落通道描述光场在大气传输中的演化过程;为研究大气闪烁对量子干涉雷达的影响机理,利用大气透射率概率密度函数描述透射率的涨落情况;利用经典湍流理论从点光强起伏的统计出发,推导了大气透射率概率密度函数P(T),并以之为基础研究了有限面积上的平均透射率和闪烁指数对量子干涉雷达灵敏度和分辨率的影响.

研究结果表明:与相干态量子干涉雷达不同,纠缠相干态量子干涉雷达无法通过调节参考光透射率克服耗散或闪烁的影响;此外,低损耗情况下系统灵敏度和分辨率性能随闪烁指数增加而降低;高损耗情况下,大气闪烁则能显著提高系统分辨率和灵敏度性能；划分分辨率和灵敏度高低损耗临界点并不一致,但二者均随平均脉冲光子数N的增加而增加.综上,大气闪烁能够在一定程度上克服大气损耗带来的不良影响.