(d,n)-余挠模与(d,n)-平坦模的环刻画

武 斌，杨晓燕

(1.兰州资源环境职业技术学院 基础学科部，甘肃 兰州 730020；2.西北师范大学 数学与统计学院，甘肃 兰州 730070)

0 引言

受以上文献的启发，文中应用(d,n)-余挠模和(d,n)-平坦模刻画这样的环R,使得每一个右R-模是(d,n)-余挠模.证明了：每一个右R-模是(d,n)-余挠模当且仅当每一个(d,n)-平坦右R-模是(d,n)-余挠模当且仅当每一个平坦维数小于等于d的右R-模M属于Pn(Pn表示投射维数小于等于n的右R-模类)当且仅当对任意m(0≤m≤n)及任何(d,n-m)-平坦右R-模M，有M∈Pm.对偶地，证明了每一个右R-模是(d,n)-平坦模当且仅当每一个循环右R-模是(d,n)-平坦模当且仅当每一个((d,n)-余挠)右R-模有具有唯一映射性质的(d,n)-平坦覆盖.另外，给出了这两类模在多项式环下的等价刻画.

1 预备知识

设M是右R-模，n和d是固定的非负整数,Fd表示平坦维数小于等于d的右R-模类，Pn表示投射维数小于等于n的右R-模类.

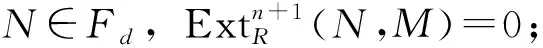
命题1[5]对于任意环R，以下结论成立：

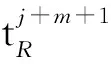
(2)右R-模M是(d,n)-余挠模当且仅当存在正合列0→M→E0→…→En→0，其中每一个Ei是(d,n)-余挠右R-模，i=0,1,…,n.

(3)Cd,n关于单同态余核封闭，Fd,n关于满同态核封闭.

定理1[5]设R是环，n和d是固定的非负整数，则(Fd,n,Cd,n)是完全遗传的余挠理论.

定义2[6]称C-包络φ:M→F具有唯一映射性质，如果对任意同态f:M→F′，其中F′∈C，且存在唯一的同态g:F→F′，使得gφ=f.

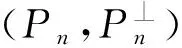
文中涉及的其他专业名词和术语均来自于文献[8-12].

2 (d,n)-余挠模与(d,n)-平坦模的应用

以下σM:M→Cd,n(M)表示右R-模M的(d,n)-余挠包络，ηM:Fd,n(M)→M表示右R-模M的(d,n)-平坦覆盖,Pd(M)表示模M的投射维数.

定理3设R是环，n,d是固定的非负整数，则以下条件等价：

(1)每一个右R-模是(d,n)-余挠模.

(2)每一个(d,n)-平坦右R-模是(d,n)-余挠模.

(3)每一个(d,n)-平坦右R-模是投射模.

(4)每一个平坦维数小于等于d的右R-模属于Pn.

(6)每一个(d,n)-平坦右R-模有具有唯一映射性质的(d,n)-余挠包络.

(7)对任意的右R-模M及任意的0≤m≤n，若M∈Fd,n-m，则M∈Pm.

(8)对任意的右R-模M,若存在0≤m≤n使得M∈Fd,n-m，则M∈Pm.

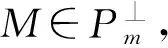
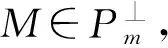
如果n≥1且(d,n-1)-余挠右R-模类关于直和封闭，则以上条件等价于下列条件：

(11)每一个(d,n-1)-平坦右R-模有单的(d,n-1)-余挠覆盖.

证明(1)⟹(6),(9)⟹(10)显然.

(1)⟹(3).由定理1得到.

(6)⟹(2).设M是(d,n)-平坦右R-模，则有以下交换图：

由Wakawatsu引理[2]知，L是(d,n)-平坦模，而σLγσM=0=0σM，于是由(6)知σLγ=0.故L=Im(γ)⊆Ker(σL)=0，所以M∈Cd,n.

(2)⟹(1).设M是右R-模，由定理1知，存在正合列0→K→N→M→0，其中K是(d,n)-余挠模，N是(d,n)-平坦模.又由(2)知N是(d,n)-余挠模.故由命题1(3)知，M是(d,n)-余挠模.

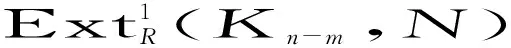
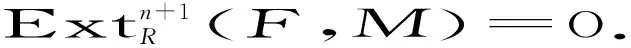
(1)⟹(11).设M是任意右R-模，记M=Σ{N≤M:N是(d,n-1)-余挠模}，G=⊕{N≤M：N是(d,n-1)-余挠模}，则存在正合列0→K→G→F→0.由(1)知，K是(d,n)-余挠模，而由假设知，G是(d,n-1)-余挠模，故F是(d,n-1)-余挠模.下证包含映射i:F→M是M的(d,n-1)-余挠覆盖.令F′是(d,n-1)-余挠模，Ψ:F′→M是任意R同态，由上面的证明知Ψ(F′)≤F.定义ε:F′→F为ε(x)=Ψ(x)，则对任何x∈F′，有iε=Ψ，故i:F→M是M的(d,n-1)-余挠予覆盖.另外,单位映射1F是使得ig=g，g:F→F的唯一映射.故(11)得证.

(11)⟹(2).设M是(d,n)-平坦右R-模，下证M是(d,n)-余挠模.由定理1知，存在正合列0→M→E→L→0，其中E是(d,n-1)-余挠模，L是(d,n-1)-平坦模.因为L有单的(d,n-1)-余挠覆盖φ:F→L，故有同态α:E→F,使得有以下交换图：

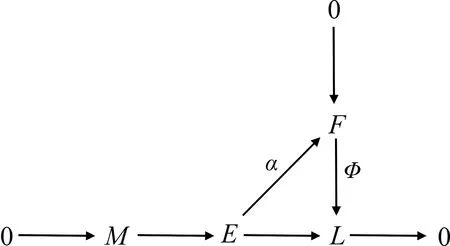
因为φ是满同态，故φ是同构，从而L是(d,n-1)-余挠模.所以M是(d,n)-余挠模. 】

推论1[4]设R是环，则以下结论等价：

(1)每一个右R-模是1-余挠模.

(2)每一个平坦右R-模是1-余挠模.

(3)每一个1-平坦右R-模是投射模.

(4)对任何平坦右R-摸M都有Pd(M)≤1.

命题2对于任意环R，以下结论等价：

(1)每一个右R-模是(d,2)-余挠模，且每一个(d,0)-平坦右R-模有(d,0)-余挠覆盖.

(2)每一个(d,0)-平坦右R-模有具有唯一映射性质的(d,0)-余挠覆盖.

证明(1)⟹(2).设M是任意(d,0)-平坦右R-模,则由(1)知，M有(d,0)-余挠覆盖f:F→M.只需证对任意(d,0)-余挠右R-模G及任意同态g:G→F，若fg=0，则有g=0.事实上，因为Im(g)⊆Ker(f)，所以有β：F/Im(g)→M，使得βπ=f，其中π:F→F/Im(g)是自然映射.因为Ker(g)是(d,2)-余挠模，则由命题1(2)知，F/Im(g)是(d,0)-余挠模.故存在α:F/Im(g)→F，使得β=fα，于是有以下交换图:

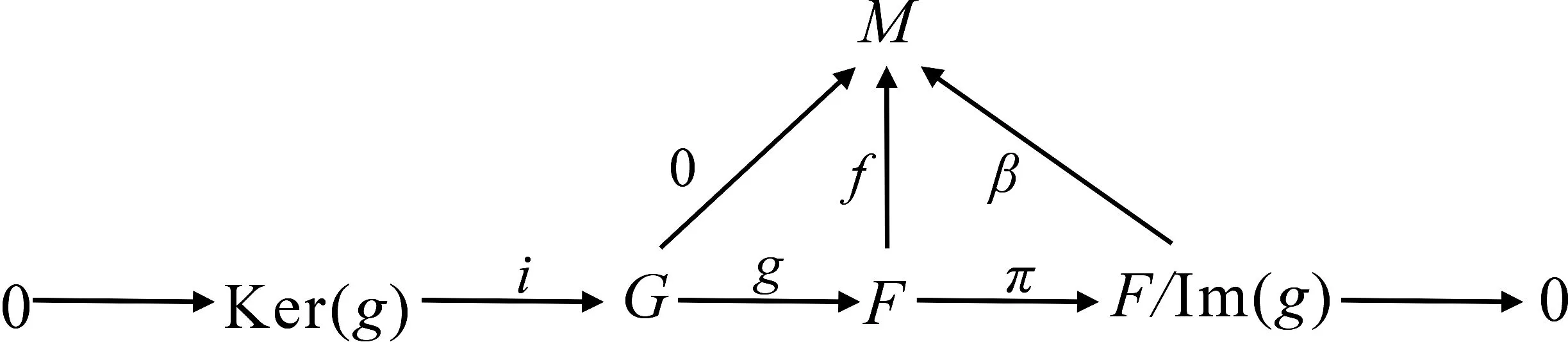
所以有fαπ=f.因为f是覆盖，故απ是同构，于是π是单同态.所以g=0.

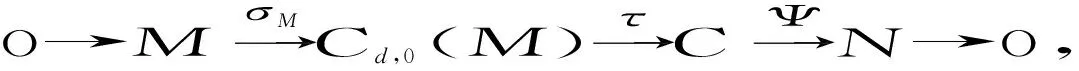
从而φγΨ=Ψ.因为Ψ是满同态，故φγ=1N.所以N同构于H的直和因子，从而N是(d,0)-余挠模.由命题1(2)知M是(d,2)-余挠模. 】

定理4设R是任意环，d,n是固定的非负整数，则以下条件等价：

(1)每一个右R-模是(d,n)-平坦模.

(2)每一个有限生成右R-模是(d,n)-平坦模.

(3)每一个循环右R-模是(d,n)-平坦模.

(4)每一个(d,n)-余挠右R-模是(d,n)-平坦模.

(5)每一个(d,n)-余挠右R-模是内射的.

(8)每一个((d,n)-余挠)右R-模有具有唯一映射性质的(d,n)-平坦覆盖.

证明(1)⟹(2)⟹(3),(1)⟹(8)及(1)⟹(4)⟺(6)⟺(7)显然.

(1)⟺(5).由定理1直接得到.

(8)⟹(4).设M是任意(d,n)-余挠右R-模,则有以下正合交换图：

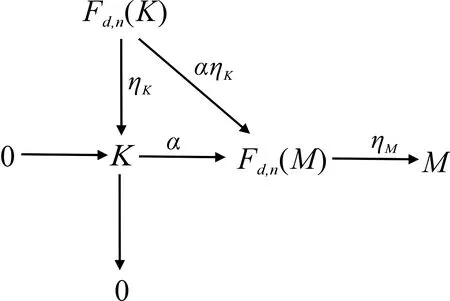
其中K∈Cd,n,ηMαηK=0=ηM0，故由(8)得αηK=0，则K=Im(ηK)⊆Ker(α)=0.所以M是(d,n)-平坦模.

(4)⟹(1).对任意右R-模M，由定理1知，存在正合列0→M→N→L→0，其中N是(d,n)-余挠模，L是(d,n)-平坦模，则由(4)知，N是(d,n)-平坦模.故由命题1(3)可得M是(d,n)-平坦模.

3 (d,n)-余挠模和(d,n)-平坦模与多项式环

设R是环，R[x]是多项式环.

定理5设R是交换环,则对任何右R[x]-模M，以下结论等价：

(1)MR是(d,n)-余挠右R-模.

(2)HomR(R[x],M)是(d,n)-余挠右R-模.

(3)HomR(R[x],M)是(d,n)-余挠右R[x]-模.

(4)MR[x]是(d,n)-余挠右R[x]-模.

证明(1)⟹(3).设F是任意一个平坦维数小于等于d的右R[x]-模，则F也是平坦维数小于等于d的右R-模，从而有

故HomR(R[x],M)是(d,n)-余挠右R[x]-模.

(3)⟹(4).因为MR[x]是HomR(R[x],M)的直和因子，所以MR[x]是(d,n)-余挠右R[x]-模.

(4)⟹(1).设F是任意一个平坦维数小于等于d的右R-模，则F⊗RR[x]是一个平坦维数小于或等于d的右R[x]-模，从而有

故M是(d,n)-余挠右R-模.

由上面的证明容易得到(2)⟺(3). 】

定理6设R是交换环，则对任何右R[x]-模N，以下条件等价：

(1)NR是(d,n)-平坦右R-模.

(2)N⊗RR[x]是(d,n)-平坦右R-模.

(3)N⊗RR[x]是(d,n)-平坦右R[x]-模.

(4)NR[x]是(d,n)-平坦右R[x]-模.

证明(1)⟹(3).设M是任意(d,n)-余挠右R[x]-模.由定理5知，M也是(d,n)-余挠右R-模，从而有

所以N⊗RR[x]是(d,n)-平坦右R[x]-模.

(3)⟹(4).因为NR[x]是N⊗RR[x]的直和因子，所以NR[x]是(d,n)-平坦右R[x]-模.

(4)⟹(1).设M是任意一个(d,n)-余挠右R-模.由定理5知，HomR(R[x],M)是(d,n)-余挠右R[x]-模,从而

故NR是(d,n)-平坦右R-模.

(2)⟺(3).显然. 】