探秘深井中的重力加速度求解方法

杨龙军

（陕西省三原县南郊中学，陕西 三原）

我们将星球当作均匀球体处理，并将球体等效为厚度不计的均匀球壳，任取一球壳，设在球壳上P点放一质量为m的质点，根据对称性，相当于形成了以P为顶点的两个对立的圆锥面。如图1所示，设P点到圆锥底面中心距离分别为r1、r2，对应底面的半径分别为R1、R2，单位面积质量为m0，则根据万有引力定律可得：

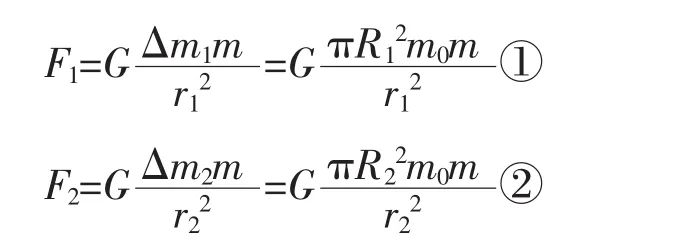
图1

联立上述三式可得F1=F2，又因为两引力方向相反，所以合力为0，以此类推，根据对称性，整个球壳对P点的引力为零。因此，质点P所受到的万有引力来源于它的内部球体对它的引力。

设总球体质量为M，半径为R，井深为d，质点P内部球体质量为M1，则可得出图2：

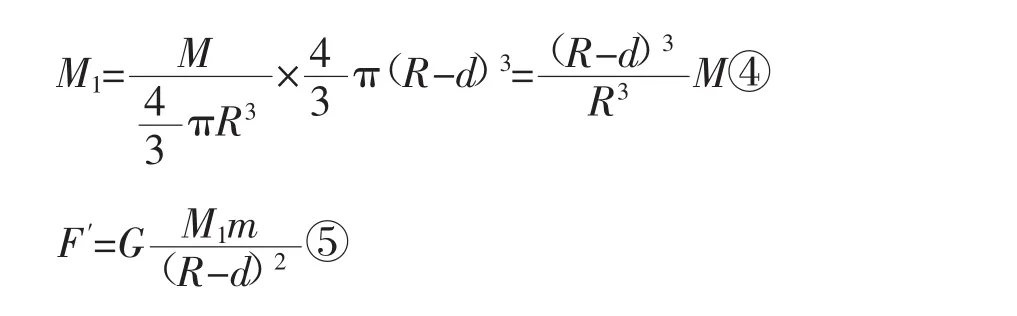
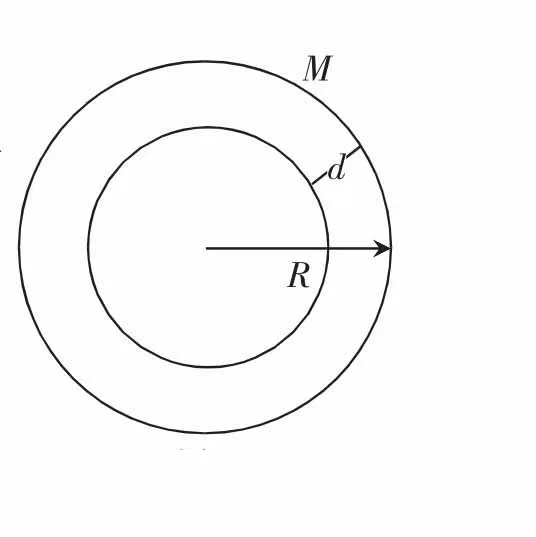
图2

希望本文的推导对学生计算重力加速度时能起到指点迷津的作用，在解题时游刃有余。