基于Matlab的倒立摆控制辅助教学实例设计

栾 卉， 孙德立， 孙慧慧， 随阳轶， 刘长英

(吉林大学 仪器科学与电气工程学院， 吉林 长春130061)

0 引言

“连续与离散控制系统”课程是我院根据教育部教学改革、学科建设和教材建设改革的精神，针对“自动控制原理”和“计算机控制原理和技术”两门课程单独开设存在的问题和弊端，将两门课整合成的一门课程，该课程列入了新版教学大纲和教学计划中，并通过我校的审批，已经连续执行了十年[1]。整合后的课程将连续与离散控制紧密和有机的结合，使学生学习具有连续性，教师在教学过程中可利用的空间变大，处理教学问题的灵活性增强，增强了学科的整体性和全局性。在总结多年改革经验的基础上，我们于2015年出版了《连续与离散控制工程》一书[2]。

“连续与离散控制系统”是我校整个工科基础课程，课程的显著特点是以数学为基础进行分析和设计，理论性强、实践性强[6]。因此它非常适合以项目教学法为基础，开展多种教学手段相结合的课程教学，这有助于激发学生学习兴趣、提高学生的科学探究能力、培养创新意识以及科学精神。为了降低控制理论的抽象性，增加直观性，我们还设计了基于Matlab的倒立摆教学辅助实例。

1 Matlab GUI 简介

图形用户界面GUI(Graphical User Interface)，又称图形用户接口。作为人与计算机通信的语言之一,它允许用户使用多种输入设备对界面上的各种空间进行操作，大大简化了人与计算机的人机交互难度。相比DOS时代的命令行的处理方式，GUI有诸多优点。GUI的控件多为标准控件，如文本框、输入框、下拉菜单和滑块等，在Matlab中这些标准控件均已被模块化，使用之前只需要学会使用Matlab的标准控件，以及能够使用C语言调用Matlab控件的回调句柄，就可以方便快捷的进行GUI的编辑。

2 倒立摆的物理模型

2.1 倒立摆的物理模型及基本假设

传统的控制方法设计大多基于对物理模型的抽象以及对抽象模型的数学建模。为了设计控制器，首先要对倒立摆进行建模，考虑到实际系统的复杂性，对仿真系统做如下理想化处理：

(1) 摆杆为刚体，不具有弹性，不发生形变;

(2) 小车与地面的滑动摩擦力与小车的速度相关系数为b;

(3) 摆杆旋转时的连接部位摩擦系数与角速度相关系数为r;

(4) 忽略电机电感,小车电机的输出扭矩正比于控制电压u比例系数默认为1。

抽象后的物理模型如图1、2所示。图1、2中各物理量如表1所示。

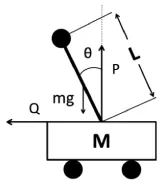
图1 倒立摆模型示意图

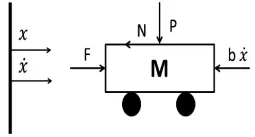
图2 小车的受力及运动示意图

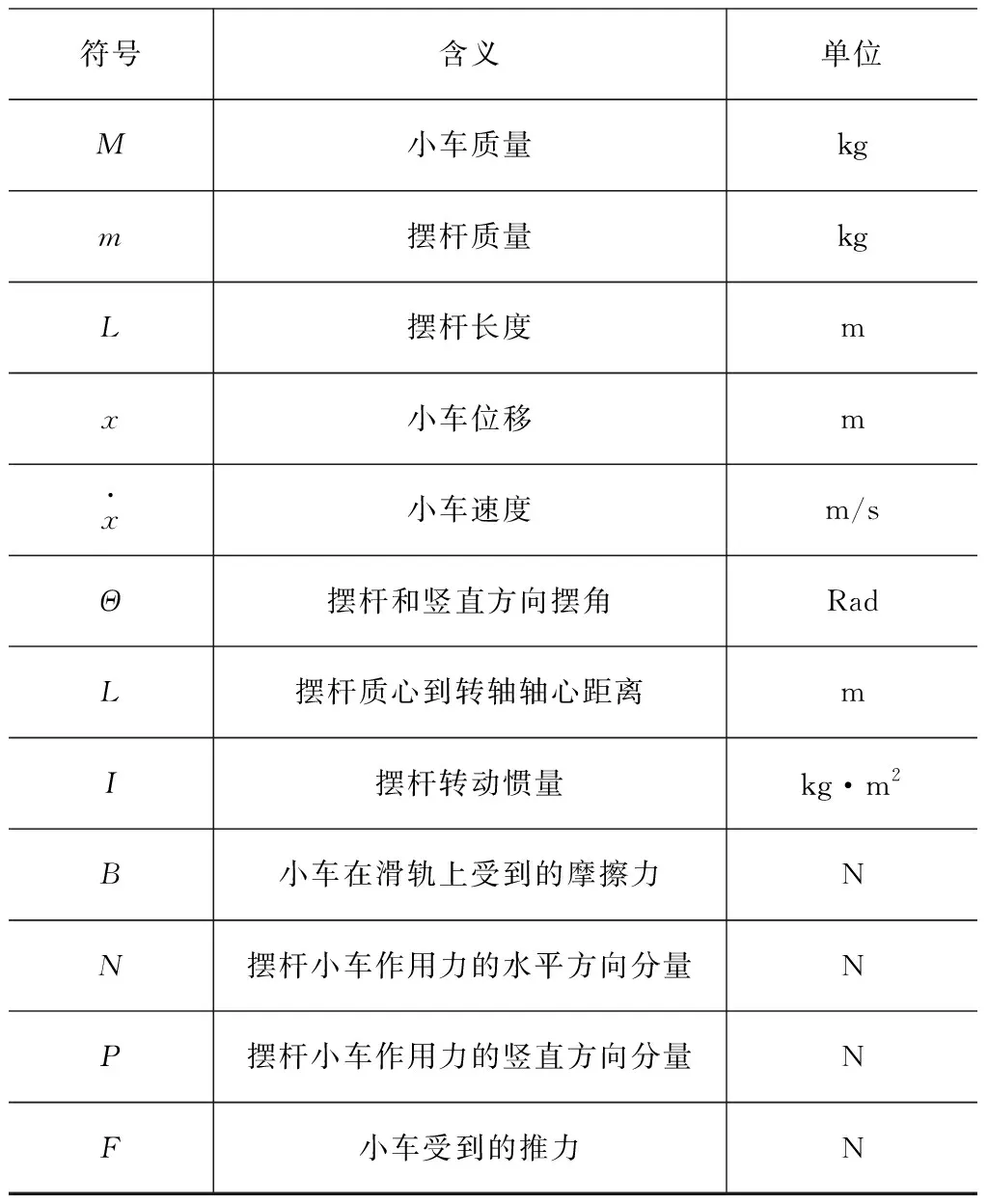
符号含义单位M小车质量kgm摆杆质量kgL摆杆长度mx小车位移mx·小车速度m/sΘ摆杆和竖直方向摆角RadL摆杆质心到转轴轴心距离mI摆杆转动惯量kg·m2B小车在滑轨上受到的摩擦力NN摆杆小车作用力的水平方向分量NP摆杆小车作用力的竖直方向分量NF小车受到的推力N

2.2 倒立摆的传递函数建模

由小车水平方向受力分析(见图2)，得到运动学方程：

Mx·=f-bx·-N

(1)

由摆杆水平方向受力分析(见图1)，得到运动学方程：

(2)

整理得

N=mx··+mlθ··cosθ-mlθ·2sinθ

(3)

把式(3)代入到式(1)中就得到系统的第一个运动方程：

(M+m)x··+bx·+mlθ··cosθ-mlθ·2sinθ=F

(4)

对摆杆竖直方向进行受力分析，得到如下的运动方程：

(5)

整理得：

p-mg=mlθ··sinθ+mlθ·2cosθ

(6)

力矩平衡方程如下：

-Plsinθ-Nlcosθ=lθ··

(7)

合并式(6)和式(7)，得到式(8)的运动方程：

(I+ml2)θ··+mglsinθ=-mlx·cosθ

(8)

根据拉格朗日法进行近似，求得被控对象的传递函数：

(9)

由于这里只考虑摆杆的角度，不对小车位置进行闭环控制，故只给出小车的开环传递函数为

G2(s)=

(10)

其中

q=(m+M)(I+ml2)-(ml)2

(11)

3 倒立摆控制演示主界面

基于Matlab的GUI开发组件，我们设计了参数可调整的单级倒立摆模型，以此模型进行了反馈控制研究，主要包括PID算法、线性二次调节器(Linear Quadratic Regulator)算法和H∞算法的控制实现。主界面由三个部分组成：参数设置部分、模型演示部分以及控制过程曲线显示部分，主界面如图3所示。

图3 倒立摆控制实例主界面

参数设置部分包括倒立摆物理模型的各项参数、各种算法的参数、仿真参数等。倒立摆模型参数包括小车重量M、摆杆质量m、摆杆长度L、小车在滑轨上的摩擦力b、摆初始角度和初始位置等，如图4(a)所示；三种控制算法的参数设置分别包括PID算法的比例系数Kp、积分常数Ki、微分常数Kd，LQR算法的权矩阵Q、 R，H∞算法的权矩阵C、R，如图4(b)、(c)、(d)所示。

(a)倒立摆初始参数 (b)LQR算法参数

(c)PID 算法参数 (d)H∞算法参数图4 参数设置部分

模型演示部分如图5所示，主要功能是按照设置的倒立摆物理参数显示模型，并能够在仿真过程中展示倒立摆的稳定过程的实时动态过程，使得学生能够更加直观地感受整个稳摆过程。

控制过程曲线显示部分如图6所示，主要显示倒立摆稳定过程中摆杆角度θ、摆杆角速度ω、小车位移x、摆杆速度V等参数的变化曲线。

4 三种控制算法教学实践

4.1 PID算法

PID控制规律为

(12)

式中Kp为比例系数，Ti为积分时间常数，τ为微分时间常数，因此Ki=Kp/Ti为积分系数,Kd=Kpτ为微分系数[2]。

分析三个参数取不同值情况下倒立摆摆杆角度随时间变化情况如图7、8、9所示。图7显示的为参数分别为：Ki=10，Kd=1，Kp=20、40、200时，摆杆角度随KP变化响应曲线。图8显示的为参数分别为Kp=200，Kd=1，Ki=0、100、600时摆杆角度随Ki变化响应曲线。图9显示的为参数分别为Kp=200，Ki=10，Kd=0、10、100时摆杆角度随Kd变化响应曲线。通过改变图4(c)所示的PID控制参数设置部件可以灵活的改变Ki、Kd、Kp的值，找到适合所研究模型的控制参数，更好的理解PID控制原理。

图5 模型演示部分

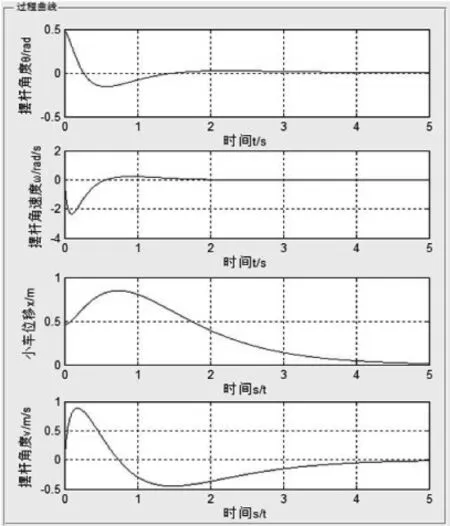
图6 控制过程曲线显示部分

图7 摆杆角度随Kp变化响应曲线

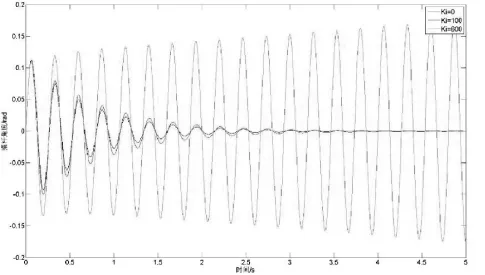
图8 摆杆角度随Ki变化响应曲线

图9 摆杆角度随Kd变化响应曲线

4.2 LQR算法

LQR控制方法目标在于在系统存在偏差时，以尽可能小的能量矫正系统，使受控变量回归正常状态。在回归稳态后使得系统的各个分量接近于期望的稳定状态。LQR控制基本原理由系统方程给出。设系统方程如下：

x=Ax+Bu

(13)

确定下列最佳控制向量的矩阵K：

u(t)=-K*x(t)

(14)

使得性能指标达到最小值：

(15)

图10 倒立摆模型的一组LQR控制参数

式中Q为正定(或正半定)艾尔米特或实对称阵，R为正定艾尔米特或实对称阵[4]，Q为受控变量的期望函数对于状态量的权重矩阵，被控量所对应的权重越大，意味着该受控量在整个系统中的控制要求更高；R阵为控制量的权重矩阵，对应的元素越大，控制约束越大，Q和R矩阵的值可以通过图4(b)所示的LQR控制器参数设置组件方便的修改，以观察不同的权矩阵值对系统输出的影响。图10为设计的倒立摆模型的一组LQR控制参数，图11为相应的系统仿真结果。

图11 倒立摆LQR控制仿真结果

4.3 H∞算法

H∞控制是针对特定双端子对象模型，一般由状态空间方程给出。设计一个闭环控制系统，使得整个系统函数的范数限制在一个期望的整数γ下，即||TY2U1(Y)||∞<γ，这时控制器的状态空间方程表示为[5]

(16)

其中

(17)

且X与Y分别为下式黎卡提方程的解

(18)

H∞理论控制的思想主要是在有限的能量输入下，寻找控制系统的最优调节器；或者在尽可能使用小的能量下使系统在有限能量的干扰下回归稳定状态。C和R矩阵的值可以通过图4(d)所示的H∞控制器参数设置组件方便的修改，以观察不同的权矩阵值对系统输出的影响。图12为设计的倒立摆模型的一组H∞控制参数，图13为相应的系统仿真结果。

图12 倒立摆模型的一组H∞控制参数

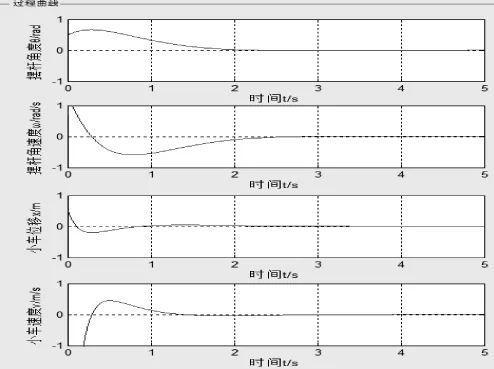
图13 倒立摆H∞控制仿真结果

5 结语

本辅助教学案例的设计将经典的倒立摆控制问题的多种控制策略整合到同一个GUI界面中，以方便对比研究不同的算法的控制效果，通过修改相应的控制参数，可以实时看到系统稳定过程的过程曲线，加深学生对于理论知识的理解，并且更直观地展示了倒立摆系统的稳定过程中摆的实时动态过程，同时该辅助教学实例也可以作为倒立摆控制系统实物设计的辅助工具。