高职高等数学中逆矩阵的求法及应用

周 同，杜珍珍

（铜陵职业技术学院，安徽 铜陵 244000）

1 引言

矩阵是高职数学线性代数的核心内容，利用矩阵研究问题，可以抓住问题的本质，简化问题的复杂程度。矩阵在自然科学、工程技术和经济管理学等多学科中都有广泛的应用。在矩阵教学过程中，经常发现学生不会求逆矩阵，而求逆矩阵是矩阵运算的一个难点。本文针对这种情况，总结了适合高职学生的常见的三种求逆矩阵的方法，并给出了逆矩阵的一些实际应用。

2 求逆矩阵的三种常用方法

2.1 定义法（待定系数法）

定义1：设A为n阶方阵，如果存在n阶方阵B，使得AB=BA=E,则称A是可逆矩阵，B称为A的逆矩阵，记作 A-1，即 B=A-1。

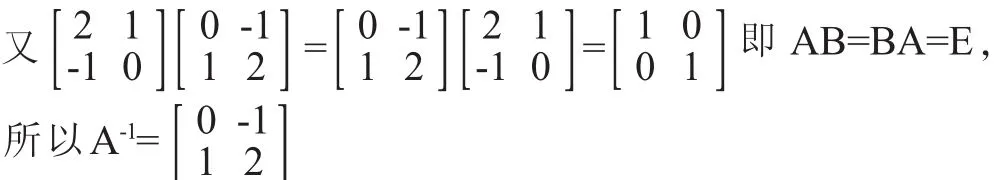
结论：定义法又称待定系数法，它是根据逆矩阵的定义，通过待定系数设逆矩阵，利用矩阵的乘法和矩阵相等的定义，通过解线性方程组就可以求得逆矩阵。在求解过程中我们可以发现，2阶矩阵求逆矩阵需要解4个方程，以此类推可知，3阶矩阵求逆矩阵需要解9个方程，4阶矩阵求逆矩阵需要解16个方程，n阶矩阵求逆矩阵需要解n2个方程，计算量相当繁琐且易出错，因此，此种方法一般应用于低阶矩阵的逆矩阵求法。

2.2 伴随矩阵法

结论：这种求逆矩阵的方法称为伴随矩阵法，求解过程中只要会求该矩阵对应的行列式的值及伴随矩阵即可代入公式计算。在求解过程中我们可以发现，3阶或3阶以上矩阵，需要求9个或9个以上的代数余子式，还要计算一个3阶或3阶以上的行列式，计算量大还很容易出错，因此，该方法一般适用于阶数不超过3阶的矩阵求逆矩阵。

2.3 初等变换法

在矩阵A的右边写一个同阶的单位矩阵E，构成一个n×2n矩阵，用初等行变换将左半部分的A化成单位矩阵E，与此同时，右半部分的E就被化成了。 同理，也可以使用初等列变换的方法，求逆矩阵，即

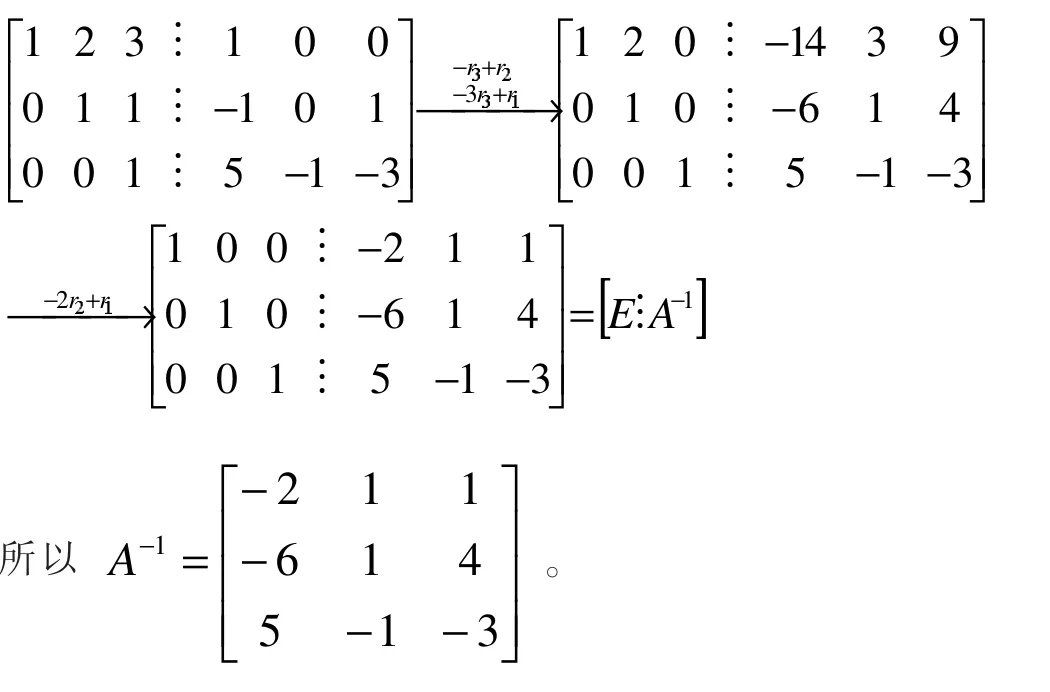
结论：初等变换法多用于三阶及三阶以上的矩阵求逆，其解题思路可归结为：1.变为上三角方阵；2.变为对角方阵；3.变为单位方阵。需要注意的是，当用初等行变换求可逆矩阵的逆矩阵时，必须始终采用行变换，绝对不可作列变换；如果在作初等行变换时，出现了零行，则说明它的行列式为零，该矩阵是不可逆的；此种方法计算过程涉及数据较多，只要一个数错了，结果就会不对，因此计算过程要求特别细心，最好对计算结果加以验证。

3 可逆矩阵的应用

3.1 在解线性方程组的应用

设线性方程组为

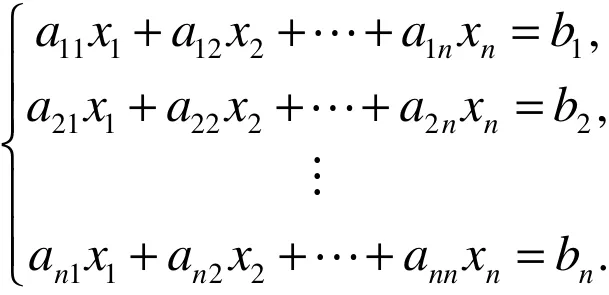
它用矩阵形式表示为AX=B

其中

对矩阵方程AX=B，两边同时左乘矩阵A的逆矩阵A-1可知：A-1AX=A-1B，而A-1A=E，得到方程的解为X=A-1B。

例4：解线性方程组

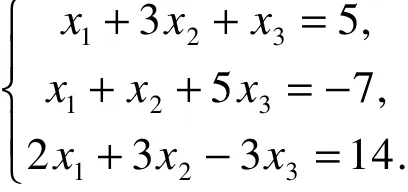
解：该线性方程组的矩阵形式为AX=B，其中

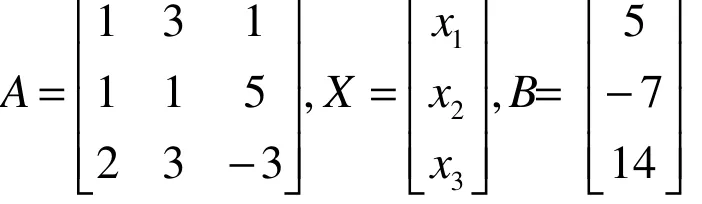
如果A-1存在，可用A-1左乘等式的两边，得A-1AX=A-1B，即，X=A-1B,

3.2 在保密通信中的应用

基于加密技术保密通信模型如下：

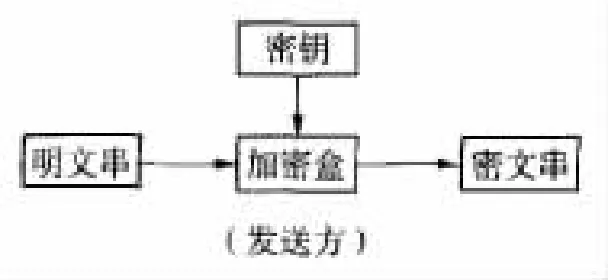
其原理是：发送方采用某种算法将明文数据加密转换成密文数据后发送给接受方，接受方则可以采用相对应的某种算法将密文数据解密转换成明文数据。

从该模型可知，一种加密技术是否有效，关键在于密文是否能还原成明文。设有矩阵方程AB=C，其中B为未知矩阵，若矩阵A可逆，则B=A-1C。故可逆矩阵可以很好地应用于加密技术。

设A为可逆矩阵，B为明文矩阵，C为密文矩阵。加密时，采用下面的矩阵乘法C=AB；解密时，采用下面的矩阵乘法B=A-1C。

例5：在学完矩阵这章后，某数学老师给本班学生发了一封密信，他有一个三阶矩阵可知矩阵A可逆，且

他们约定：消息的每一个英文字母用一个整数来表示：

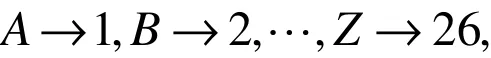
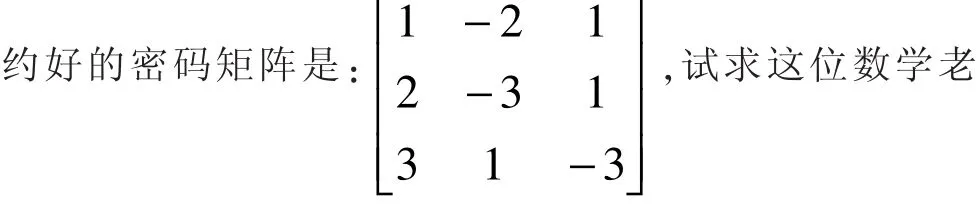
师发给学生的密信的内容。

解：设密信内容矩阵为X，则：

由英文字母和整数间的对应可得到密信内容为“I LOVE MATH”。

4 结束语

鉴于高职学生数学基础差，学习积极性不高，总感觉学习数学是无用的，本文给出了适合高职学生的求逆矩阵的三种方法，通俗易懂，然后利用逆矩阵知识去解决一些实际问题。这样，让学生感觉学习数学不是枯燥无用的，它在我们实际生活中有很重要的作用。