Zinc isotope fractionation under vaporization processes and in aqueous solutions

·

Abstract Equilibrium Zn isotope fractionation was investigated using first-principles quantum chemistry methods at the B3LYP/6-311G*level.The volume variable cluster model method was used to calculate isotope fractionation factors of sphalerite,smithsonite,calcite,anorthite,forsterite,and enstatite.The water-droplet method was used to calculate Zn isotope fractionation factors of Zn2+-bearing aqueous species; their reduced partition function ratio factors decreased in the orderGaseous ZnCl2was also calculated for vaporization processes.Kinetic isotope fractionation of diffusional processes in a vacuum was directly calculated using formulas provided by Richter and co-workers.Our calculations show that in addition to the kinetic isotope effect of diffusional processes,equilibrium isotope fractionation also contributed nontrivially to observed Zn isotope fractionation of vaporization processes.The calculated net Zn isotope fractionation of vaporization processes was 7–7.5‰,with ZnCl2as the gaseous species.This matches experimental observations of the range ofZn isotope distribution of lunar samples.Therefore,vaporization processes may be the cause of the large distribution of Zn isotope signals found on the Moon.However,we cannot further distinguish the origin of such vaporization processes;it might be due either to igneous rock melting in meteorite bombardments or to a giant impact event.Furthermore,isotope fractionation between Zn-bearing aqueous species and minerals that we have provided helps explain Zn isotope data in the fields of ore deposits and petrology.

Keywords Evaporation process⋅Zinc isotope⋅Kinetic isotope fractionation⋅Equilibrium fractionation⋅Zinc species in solution

1 Introduction

Zinc(Zn)is a transition element with atomic number 30.Its abundance in the upper continental crust is about 71 μg/g(Taylor and McLennan 1995;Cloquet et al.2008).Zinc is the second most abundant transition metal in the deep ocean,with a concentration of up to 15 nmol/L(Cloquet et al.2008).In nature,Zn mainly exists in sulfides;the predominant Zn-bearing mineral is sphalerite(cubic ZnS),with smithsonite(ZnCO3)and hemimorphite also fairly common.

Zinc has five stable isotopes—64Zn,66Zn,67Zn,68Zn,and70Zn—with abundances of 49.19%,27.79%,4.04%,18.39%,and 0.60%,respectively(Tanimizu et al.2002).The average atomic mass of Zn is 65.37777(Ponzevera et al.2006),but there is controversy over its absolute value(Rosman 1972,b);Chang et al.2001).Blix et al.(1957)and Rosman(1972)were the pioneers in studying Zn content of different samples.At the time,they found no Zn isotope composition changes in terrestrial samples due to limitations of available analysis techniques.However,with the development of multiple collector-inductively coupled plasma-mass spectrometry(MC-ICP-MS),isotope analysis precision has increased substantially,enabling us to make more precise measurements of Zn isotope composition.Maréchal et al.(1999) first utilized ICP-MS to analyze Zn isotope composition of terrestrial and biological samples.Their results indicate that Zn isotope composition variations are common in natural samples.In the past several years,the study of Zn isotopes has been widely applied to many fields,such as astrochemistry (Luck etal.2005,2006;Moynier et al.2006,2007;Herzog et al.2009,2010,2011),geology(Maréchal et al.1999;Mason et al.2005;Wilkinson et al.2005;John et al.2008;Moynier et al.2009;Pons et al.2013),environmental chemistry(Bermin et al.2006;Vance et al.2006;Weiss et al.2007),and biology(Maréchal and Albarède 2002;Zhu et al.2002).

It is noteworthy that Zn is a moderately volatile element,i.e.,with a half-mass condensation temperature(Tc)(at 10-4bar)between 1250 and 650 K(Palme et al.1988).The moderate volatile elements include P,Mn,Li,As,Sb,Ga,Na,Cl,B,Ge,Rb,F,Zn,Te,Sn,Se,and S.Several different Tc results of Zn have been published:684 K at 10-4bar,668 K at 10-6bar(Wai and Wasson 1977),and about 730 K at 10-4bar(Lodders 2003).These results suggest that Zn-bearing species can be volatilized and sublimated to the gas phase easily at temperatures of 400–700 °C.

The study of Zn isotope fractionation opens a door to investigate the details of evaporation processes in which Zn-bearing compounds are involved.Volatile elements play a key role in the chemical evolution of planets.From previous studies we know that the Moon is volatile-depleted and stable isotope fractionation of moderately volatile elements could have happened during the giant impact event of Moon formation(Humayun and Clayton 1995;Albarède 2009).Previous studies have also shown that Zn isotopes could be largely fractionated in vaporization processes of other terrestrial planetary bodies(e.g.Moon),but only marginally fractionated during igneous processes of the Earth(Moynier et al.2006,2009,2011;Albarède 2009;Paniello et al.2012).Therefore,Zn has become a very popular element in investigations of the evaporation processes associated with the giant impact.In addition,Zn isotope fractionation has been found to be larger in samples with low Zn concentrations than those with high Zn concentrations;in other words,the isotope composition of Zn is negatively correlated to elemental abundance(Paniello et al.2012).

Isotope tracing is an important method in ore deposit investigation.From the perspective of metallogeny,traditional stable isotopes such as H,C,O,and S are often indirectly related to the source of metals,i.e.,the main body of ore deposits.Therefore,more and more studies are using non-traditional isotope systems(e.g.,Cu,Fe,Zn)to study ore deposits.In the past several years,developments in Zn isotope analysis techniques have made it possible to utilize Zn isotopes to trace the formation of Zn-bearing deposits(Albarède 2004;Mason et al.2005;Wilkinson et al.2005;John et al.2008).However,these studies indicate that Zn isotope fractionation is small(＜ 0.5‰)relative to other transition metals(those having more than two redox states)such as Fe(about 5‰).This is because Zn has only one common oxidation state(Zn2+)(Dauphas and Rouxel 2006;Gagnevin et al.2012).

Meanwhile,Zn plays an important role in the interaction between biosphere and geosphere.If the concentration of Zn exceeds a threshold,it can cause environmental pollution.The study of Zn distribution has a number of applications in investigations of organic evolution and environmental pollution(Novak et al.2016).

In this study,we used quantum chemistry to obtain basic Zn isotope fractionation factors of different Zn-bearing substances.These factors can be useful for people studying Zn isotopes in several geoscience subdisciplines.We also applied these Zn isotope fractionation factors to explain the vaporization processes observed on the Moon.

2 Theory and methods

2.1 Equilibrium isotope fractionation calculation

The Bigeleisen–Mayer equation or Urey model(Bigeleisen and Mayer 1947;Urey 1947)is the cornerstone of theoretical and computational stable isotope geochemistry,revealing the equilibrium isotope exchange constant K.Take a simple isotope exchange reaction as an example:

where A and B stand for two kinds of substances,A*and B*are the substance with heavier isotopes relative to A and B,respectively.The reaction equilibrium constant,K,can be obtained from the ratio of the reduced partition function ratios(RPFRs)of these two substances:

In the field of geochemistry,the isotope fractionation factor,α,is used instead of K.The relationship between α and K is α=K1/n,where n is the number of atoms exchanged during the isotopic exchange reaction.If there is only one isotope exchanged during the reaction,then α=K.In most cases,because α is very close to 1.0,the isotope fractionation factor between A and B is approximately ΔA–B≈ 103*lnα.The expression of RPFR can be calculated as:

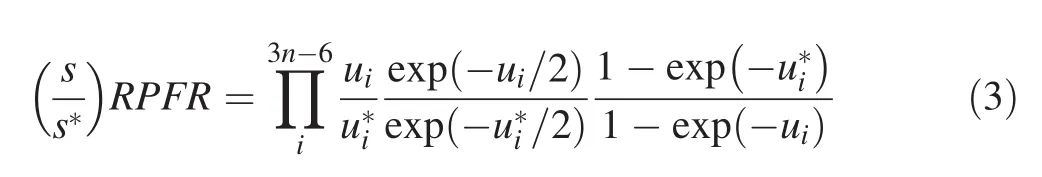
where s is the symmetry number of the molecules or clusters.In this study,s=s*.The asterisk stands for the molecules with heavier isotopes.And uican be obtained from the harmonic vibrational frequencies,vi:

where h,kb,and T are the Planck constant,the Boltzmann constant,and temperature in Kelvin,respectively.Based on this model,the equilibrium isotope fractionation factor can be obtained via the harmonic vibrational frequencies of two substances and the magnitude of isotope fractionation is related to the temperature.Under extremely high temperature,isotope fractionation will be very small and even become negligible.

One of the key factors in isotope fractionation calculation is precise harmonic frequencies of different isotopologues. With the tremendous developments in computational quantum chemistry,it is possible to calculate the harmonic vibrational frequencies of macromolecules,molecule clusters,and even condensed phases.Those harmonic frequencies are exactly what the Bigeleisen–Mayer equation requires(Liu et al.2010).Consequently,using ab initio or first-principles methods to calculate isotope fractionation factors is becoming a routine job(Driesner and Seward 2000;Oi 2000;Oi and Yanase 2001;Jarzecki et al.2004;Schauble 2004;Anbar et al.2005;Liu and Tossell 2005;Tossell 2005;Zeebe 2005;Schauble et al.2006;Rustad and Bylaska 2007;Schauble 2007;Seo et al.2007;Otake et al.2008;Rustad et al.2008;Rustad and Zarzycki 2008;Fujii et al.2009a,b,2010,2011;Fujii and Albarède 2012;Li et al.2009;Li and Liu 2011;Li and Liu 2010;Black et al.2011;Pons et al.2013).Researchers often need to implement scaling treatment to obtain reasonable harmonic vibrational frequencies of different molecules(Hehre 1986).Several previous studies focused on improving the Bigeleisen–Mayer equation by adopting higher-level anharmonic corrections(Richet et al.1977;Bigeleisen 1996,1998;Liu et al.2010).For a transition metal isotope system like Zn,its anharmonicity is small and those corrections are unnecessary.In this study,Gaussian03 and Gaussian09 software were used for all calculations(Frisch et al.2003,2009).

2.2 Isotope fractionation calculation of diffusion process in vacuum

Both equilibrium and physical kinetic processes can affect isotope fractionation.Here,we introduce methods to calculate diffusional isotope fractionation,which is a physical kinetic process.The theoretical expression of the molecular diffusion coefficient is defined from the Chapman–Enskog theory(Chapman and Cowling 1991):

where Dm,N,M,and T are the molecular diffusion coefficient,atmospheric density,average mass of the environmental material,and temperature in Kelvin,respectively.σ0is a factor depending on the collision integral and molecular radius,and m is the mass of the interested atom.

In the gas phase,the widely used definition of the isotope fractionation factor during the diffusion process is equal to the quotient of the molecular diffusion coefficients of different isotopologues:

where mHand mLare the particles(molecules)with heavy and light isotope atoms,respectively.If the molecules are diffused into a vacuum,M is approximately equal to the lighter isotopologues.In other words,M≈mL.Therefore,

The expression above is similar to the equation obtained by Richter et al.(2007):

where i and k indicate particles with atoms of different atomic mass.In fact,the term of the kinetic isotope fractionation factor includes the evaporation coefficient ratio of different isotopologues(i.e.γi/γk,)where γ is the evaporation coefficient.There is an assumption that different isotopologues of a given element have similar evaporation coefficients(Richter et al.2007).Equation(8)has been used by a lot of researchers in the domain of geochemistry and astrochemistry(Davis et al.1990;Richter et al.2002,2007,2009;Young and Galy 2004;Paniello et al.2012).

Richter et al.(2007)deduced the expression of isotope fractionation factor of evaporation processes through the method of flux,and indicated that it could be divided into two parts—equilibrium fractionation and physical kinetic fractionation,i.e.:

where αevap,αeq,and αkinare the total isotope fractionation factor during the evaporation process,the equilibrium fractionation factor,and the kinetic fractionation factor,respectively.The equilibrium fractionation factor can be calculated through the Urey model,which will be illustrated in the following section.

2.3 The volume variable cluster model method

In this study,Zn-bearing minerals were simulated by a cluster-model-based method,known as the volume variable cluster model(VVCM)method(He and Liu 2015;Li and Liu 2015;He et al.2016).Molecular clusters can be used to represent mineral environments(Gibbs 1982).The isotope effect is indeed a local effect mostly affected by the next nearest neighborhood atoms(i.e.,the NNN rule).With a cluster size larger than this threshold,the isotope effect of the interested atom can be properly addressed.

VVCM was proposed to improve a similar method suggested by Rustad et al.(2010).The largest difference between them is that a fixed layer of atoms in the model of Rustad et al.(2010)has been removed and all the atoms in the VVCM are freely optimized.This treatment is used to remedy possible false tensions produced by fixed-volume treatment and the use of different theoretical levels for aqueous and solid species.Under VVCM,the whole cluster is freely optimized to the lowest energy point and the same theoretical level is used for both aqueous and solid species.

For VVCM,several rules must be followed to produce reasonable results.First,the interested atom(here,Zn)is always placed at the center of the cluster model.Second,hundreds of virtual charges are needed around the cluster to electronically neutralize it.The distance and positions of the out most atoms and virtual charges are adjustable to let the cluster find a minimal energy point from full optimization.The B3LYP/6-311G*level was used for all Znbearing species studied here.Cluster models of sphalerite,anorthite,enstatite,and calcite with Zn atoms at the center are shown in Fig.1.

2.4 The solvation effect calculation

In this study,the water-droplet method was used to model the solvation effect in aqueous solutions,i.e.,Zn2+cation was surrounded by a number of water molecules or ligands to model its chemical environment in solution.For example,when attempting to calculate Zn2+in diluted aqueous solutions,its first coordination shell structure must be based on experimental evidence.Because[Zn(H2O)6]2+is the dominant species of aqueous Zn2+(Black et al.2011),we first put six water molecules surrounding the Zn2+ion to form an octahedral-like structure.These six water molecules were treated as the first shell of waters of this complex.After optimizing this structure,another six water molecules were added to the optimized[Zn(H2O)6]2+structure to form[Zn(H2O)6]2+(H2O)6.These new water molecules were all placed at the second-coordination shell of Zn2+.Then this structure was optimized again.By this procedure,we obtained the most stable structure of[Zn(H2O)6]2+(H2O)24,and then calculated its harmonic vibrational frequencies.Note that the geometry optimization and frequency calculation processes must be under the same theoretical level.Even though significant time was required to optimize geometries and calculate frequencies,from our experience,it is improper to pre-optimize the geometry at a lower level first,then re-optimize it at a higher level in order to save time.Inaccurate local structures are often produced by lower theoretical levels and cannot be corrected under higher levels due to the minimal search limitation of current methods.

3 Results and discussion

3.1 Zinc isotope fractionation in the evaporation process

3.1.1 Equilibrium zinc isotope fractionation in the evaporation process

The Earth and Moon have identical isotope compositions of oxygen and refractory elements such as Cr,W,and Ti.The results of Paniello et al.(2012)indicate that the isotopic compositions of volatile elements on the Moon are very different from those of Earth.The variation range of lunar sample isotope compositions is up to 8%,while it is mostly around zero for Martian meteorites and terrestrial igneous rocks.They attributed these differences to the evaporation caused by the Moon-forming giant impact event,during which the Moon was enriched with heavy Zn isotopes.On the planetary scale,Zn is one of the few elements that is different in lunar and terrestrial basalt samples.This difference may be caused by evaporation processes,as many studies have suggested that magmatic differentiation could not cause large Zn isotope fractionation.

Evaporation(similar to condensation)is a very important process for studying the formation of the Moon and the chemical evolution of planets.There have been many studies on isotopic fractionation during evaporation or condensation(Luck et al.2005,2006;Moynier et al.2006,2007,2010,2011;Herzog et al.2009;Paniello et al.2012).Data from meteorites indicate that Zn is compatible with Mg in silicates and anorthite,which are the main hostsof Zn in lunar samples.Therefore,we chose to analyze forsterite,enstatite,and anorthite by VVCM with the center metal atoms substituted by Zn(Lodders 2003;Liu et al.2006)to simulate these Zn-bearing solid minerals.The RPFRs of these minerals decreased in the sequence enstatite＞forsterite＞anorthite(Fig.2).Previous results have shown that the evaporation product of Zn was ZnCl2(g)(Chou et al.1975).Hence,we considered the whole isotopic exchange reaction during the evaporation as:

Fig.1 Cluster models of sphalerite,anorthite,enstatite,and calcite with Zn atoms at the center

The equilibrium isotope fractionation factors between the solid phases and gas phase were obtained through the Bigeleisen–Mayer equation.The relationship between the equilibrium fractionation factors and temperaturesis shown in Fig.3.These results show that during the evaporation processes,the gaseous phase(ZnCl2)preferentially enriched heavier Zn isotopes relative to the solid phase except for enstatite,which slightly enriched heavier isotope relative to ZnCl2.The magnitudes of equilibrium Zn isotope fractionation between gas and condensed phases were about+0.3,+2 and-0.18‰ at 25 °C for forsterite,anorthite,and enstatite,respectively.Isotope fractionation decreases as temperature increases and if the temperature is high enough,the equilibrium isotopic fractionation becomes negligible.

Fig.2 Reduced partition function ratios of enstatite,forsterite,smithsonite,sphalerite,calcite,and anorthite(the center atoms are substituted by Zn)as a function of temperature at B3LYP/6-311G*level

Fig.3 Equilibrium Zn isotope fractionation factors versus temperature at the B3LYP/6-311G*level

3.1.2 The total isotope fractionation of zinc during evaporation processes

For a process like Zn-bearing compounds evaporating in a vacuum,the kinetic isotope fractionation factor can be calculated using Eq.(8).In this study,the gas species was ZnCl2(g).The kinetic Zn isotope fractionation factor caused by diffusion in a vacuum was about 0.993.The total isotope fractionation factor of Zn during the evaporation process is approximately equivalent to the equilibrium isotope fractionation factor times the kinetic fractionation factor,i.e., αevap= αeq*αkin(Richter et al.2007).The fractionation factors of Zn-bearing substances during evaporation processes are plotted as a function of temperature in Fig.4.

If there is a reservoir effect,Zn isotope fractionation between vapor and condensed phases can be determined using the Rayleigh distillation model:

Fig.4 Zn isotope fractionation factors of evaporation processes between gaseous ZnCl2and solid phases as a function of temperature

where R is the isotopic ratio of the residual(solid)phase,R0the initial isotopic ratio of the isotope,f the fraction of this isotope remaining in the condensed phase,and αevapthe apparent isotope fractionation factor of the whole evaporation process.If Rayleigh fractionation is expressed in the form of δ,then

where the subscripts ‘‘ final’’and ‘‘initial’’stand for the isotope compositions of the final and initial state in units of permil(‰).In most experimental situations,the initial isotope composition,δ,of Zn is known and the isotope composition of the final state can be acquired by experimental method,hence the fraction of isotope remaining in the condensed phase can be calculated.

In previous study,the isotope fractionation factor of Rayleigh distillation only used the square-root of the mass of different isotopologues.However,the experimental values are smaller than the theoretical ones.In our method,we introduced the equilibrium isotope fractionation factor into the isotope fractionation factor of evaporation used in the Rayleigh equation.We offer a theoretical explanation that equilibrium isotopic fractionation could vary in a negative direction to kinetic isotopic fractionation.Previous studies have suggested that the isotope fractionation factor of the evaporation process is 0.993;however,our results indicate that equilibrium isotope fractionation(of forsterite and especially anorthite)also plays a nontrivial role in the overall fractionation of the evaporation process(Fig.4),largely because Zn can be vaporized at lower temperatures.In the case of enstatite,the total isotope fractionation factor was slightly higher than the kinetic isotope fractionation factor.Previous research has shown that the vast majority of plagioclase is anorthite in Moon rock samples;hence,the total isotope fractionation factor would be smaller if we considered equilibrium isotope fractionation.

The calculated net Zn isotope fractionation of vaporization processes was about 7–7.5‰ (Fig.4),with ZnCl2as the gaseous species.This matches the experimental observations of the range of Zn isotope distribution of lunar samples(e.g.,Paniello et al.2012).Therefore,vaporization processes may be the cause of the large distribution of Zn isotope signals found on the Moon.However,we cannot further distinguish the origin of such vaporization processes.It might be due either to common igneous rock melting or to a giant impact event.

Fig.5 The first coordination shells of Zn2+in aqueous solution.a–f represent the aqueous species of ，respectively.Zinc atoms are shown in indigo;oxygen in red;chlorine in green;and hydrogen in white

3.2 Speciation and isotope fractionation factors of Zn2+in aqueous solutions

One of the reasons that Zn isotope compositions have a small distribution for Earth samples is that there is water on Earth.Zinc can be easily dissolved into solution,especially brines.From experiments,direct structure information about aqueous Zn species can be obtained through visible,infrared,and ultraviolet spectra;Raman spectrum;X-ray diffraction;X-ray absorption;and neutron scattering.Most of these studies require a relatively large number of samples for analysis.Anderson et al.(1998)pioneeringly used X-ray absorption fine structure(XAFS)to investigate metal halide in fluid inclusions.

The speciation of Zn2+in aqueous solutions is related to the different types of ligands,ligand concentrations,and pH(Maréchal and Albarède 2002;Black et al.2011).Liu et al.(2011)used ab initio molecular dynamics to investigate the hydration of Zn2+in hydrothermal fluids.Investigations of natural fluid inclusions have indicated that the predominant species in hyper-saline brines up to 430°C is tetrahedral ZnCl4(Anderson et al.1995,1998),a finding con firmed qualitatively by Mayanovic et al.(1999).However,in most cases,the chief speciation of Zn2+complex is[Zn(H2O)6]2+in diluted aqueous solutions(Black et al.2011).In addition,the coordination between Zn2+and other inorganic ligands(such as chloridion,hydrogen sulfide,and hydroxyl)are also very important because water molecules are always replaced by halogen or sulfide species or other anionic ligands in ore-forming fluids or seawater(Liu et al.2011).Therefore,the coordination forms of Zn complexes in brine are very complicated;meanwhile,the concrete geometries of Zn complexes play a key role in understanding the geochemical behavior of Zn2+cations.

The optimized first-coordination shell structures of different aqueous Zn2+species are shown in Fig.5,and their Zn–O and Zn–Cl bond-length results are shown in Table 1.From the optimized geometries and previous studies on aqueous Zn2+complexes(Black et al.2011),a conclusion could be drawn that aqueous Zn2+is always hexa-coordinated with water molecules(i.e.,[Zn(H2O)6]2+).Otherwise,if there are Cl-ions in the first coordination shell of Zn2+,it can be 6-,5-,or 4-ccordinated,such as[ZnCl2(H2O)4],[ZnCl3(H2O)2]-,and[ZnCl4]2-.

The optimized geometry of[Zn(H2O)6]2+places it in the symmetry point group Th(Fig.5).The optimized Zn–O bond length was about 2.10 A˚,slightly larger than experimental results(2.08–2.09 A˚),but better than results obtained by a previous calculation(Parchment et al.1996).Table 1 shows optimized Zn–O and Zn–Cl bond lengths of all aqueous Zn species studied.In the structure of[ZnCl(H2O)5]+,the five Zn–O bonds were slightly different from each other and the axial Zn–O(2.06 A˚)bond was very close to the experimental value(2.07 A˚).

Owing to the importance of understanding Zn isotope fractionation in natural samples,it is necessary to study Zn isotope fractionation in solution systematically.Researchers have found that the different forms of metal-bearing species can affect isotopic fractionation(Hill et al.2009;Fujii et al.2010).The complexes of Zn2+in aqueous solutions coordinated with chloridion were calculated by Fujii et al.(2009a,b,2010).Schauble(2003)researched Zn isotope fractionation factors between minerals and Zn2+aqueous solutions and the latest article about the theoretical calculation of Zn isotopes is by Black et al.(2011).

Complexes with different ligands or different coordination numbers of the same ligands have different isotope fractionation factors.A different number of ligands(such as water)in the inner layer of complexes in aqueous solutions can also produce various isotope fractionation factors.Therefore,the isotope fractionation factors between different Zn-bearing species which exist in aqueous solutions and their precipitated solids(e.g.,ZnS,ZnCO3,and Zn(0))will be absolutely different.

In this study,we mainly investigated the complexes of Zn that coordinated with water and chlorine.In most Zn2+–Cl aqueous solutions,the possible species are[Zn(H2-O)6]2+,[ZnCl(H2O)5]+,[ZnCl2(H2O)4],[ZnCl3(H2O)2]-,and[ZnCl4]2-.To obtain more accurate and reasonable results,four different possible local con figurations were used to simulate Zn2+aqueous species(with subscripts A,B,C,and D).These species were surrounded by up to 24water molecules to include solvation effects.Before arriving at the final structure of Zn2+complexes such as[Zn(H2O)6]2+⋅24H2O,a series of water-droplets were optimized with 6,12,and 18 water molecules.The RPFRs of the four different con figurations were slightly different from each other although they were surrounded by the same number of water molecules(see Table 2).All the structures of these water-droplet clusters are shown in Fig.6.The average RPFR value of the four different con figurations was taken as the final result(see Fig.7).

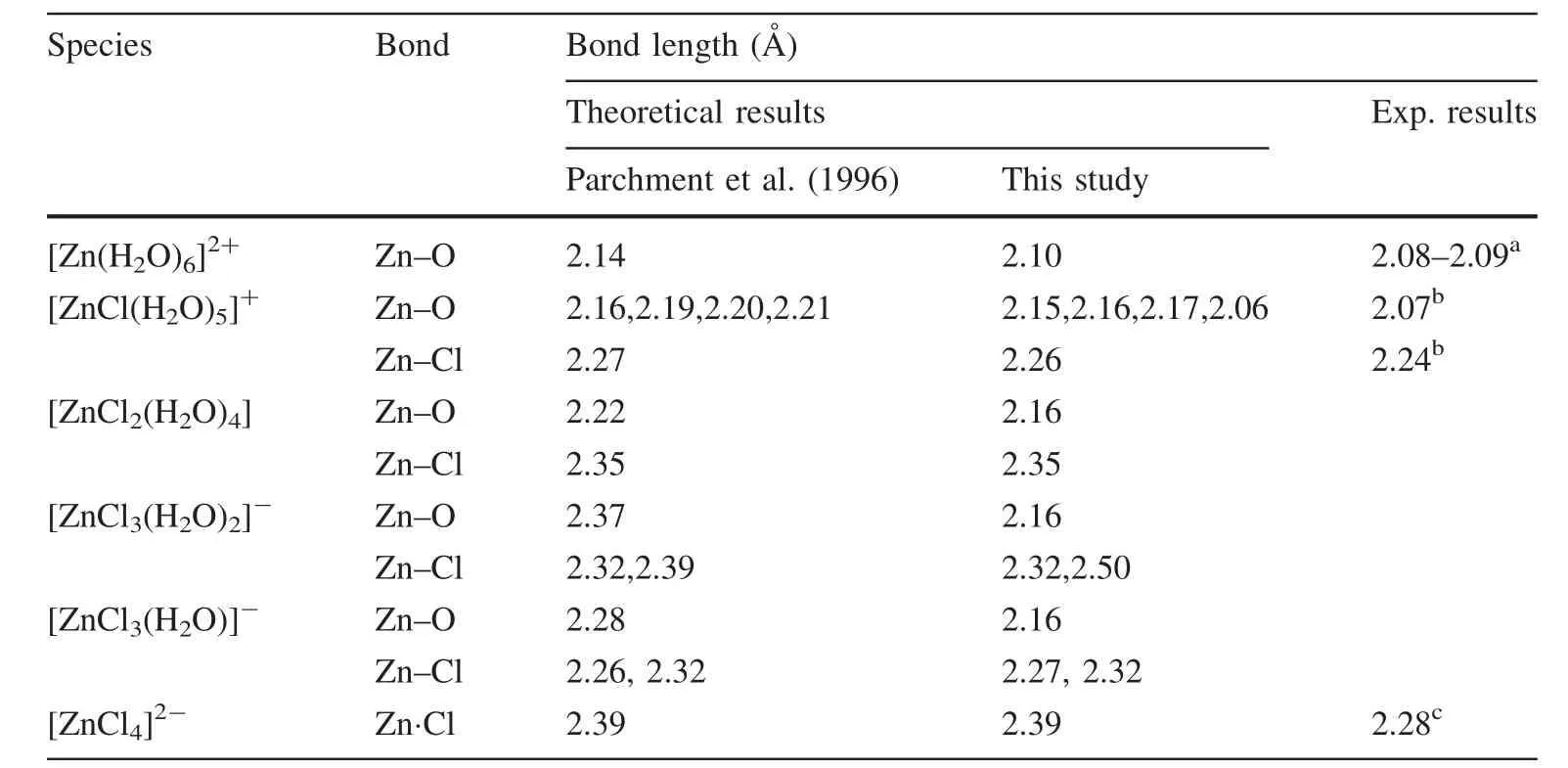
Table 1 Calculated and experimental bond lengths of different Zn2+species in aqueous solutions

The results show that the RPFRs of different Zn2+species decreased with an increased number of chlorine ligands,i.e.,[Zn(H2O)6]2+⋅24H2O had the biggest RPFR,while[ZnCl4]2-⋅24H2O had the smallest.This can be explained by the difference between the different ligands,i.e.,H2O and Cl.Our calculation level was different from that used in Black et al.(2011).Our results were slightly different from those of Black et al.(2011).Taking the RPFR of[Zn(H2O)6]2+⋅24H2O(0 °C)as an example,their results are 4.42,4.41,4.55,4.50,and 4.49(B3LYP/LANL2DZ&6-31G*)while our results were 4.70,4.56,4.74,and 4.74(B3LYP/6-311G*)for all aqueous Zn2+species studied.For all the water droplets of Zn complexes,the vibration frequencies of the structures had no negative frequencies in our method.Therefore,the results obtained in this study are reasonable compared to previous studies,which had some negative frequencies.

Table 2 Calculated 1000*ln(RPFR)values(in terms of66Zn/64Zn)for[Zn(H2O)6]2+⋅24H2O,[ZnCl(H2O)5]+ ⋅24H2O,[ZnCl2(H2O)4]⋅24H2O,[ZnCl3(H2O)2]- ⋅24H2O,and[ZnCl4]2- ⋅24H2O

Fig.6 Optimized structures of different species of Zn2+ in aqueous solutions. a–e representrespectively

Fig.7 Reduced partition function ratios for different species of aqueous Zn2+as a function of temperature

Table 3 Isotopic fractionation of zinc(in terms of66Zn/64Zn)between smithsonite and sphalerite

3.3 Isotope fractionation factors of zinc between different substances

3.3.1 Zinc isotopic fractionation between different minerals

Zinc mainly exists in the minerals of sphalerite and smithsonite,which can co-exist on Earth.Therefore,investigation into the isotope fractionation factor between these two important Zn-bearing minerals could give us their formation temperature.Previous studies have reported that smithsonite may be heavier than sphalerite by up to 0.3‰ (at about 200 °C)(Albarède 2004).In this study,the calculated results suggest that smithsonite is isotopically heavier than coexisting sphalerite and the Zn isotope fractionation factor varied from 0.37 to 0.24 in the temperature range of 100–200 °C.Our results are consistent with experimental values(Table 3 and Fig.2).

Fig.8 Zinc isotope fractionation factors between minerals and aqueous Zn2+as a function of temperature.Black lines represent sphalerite versus aqueous Zn2+.Blue lines represent calcite versus aqueous Zn2+.Square,diamond,upright triangle,asterisk,and inverted triangle represent[ZnCl4]2-⋅24H2O,[ZnCl3(H2O)2]-⋅24H2 O,[ZnCl2(H2O)4]⋅24H2O,[ZnCl(H2O)5]+⋅24H2O,and[Zn(H2O)6]2+⋅24H2O,respectively

3.3.2 Zinc isotopic fractionation between sphalerite,calcite,and aqueous solutions

Hydrothermal ore deposits are very important due to their economic significance.Sphalerite or calcite can be precipitated from hydrothermal fluids.Kinetic(e.g.,rapid precipitate)and equilibrium isotope effects occur during this process.From the investigations above,the predominant species of Zn in hydrothermal fluid are[Zn(H2O)6]2+⋅24H2O and[ZnCl4]2-⋅24H2O,and the solid phases are sphalerite and calcite.In this section,we calculated the equilibrium isotope fractionation factors between solid phases(sphalerite and calcite)and hydrothermal fluids at different temperatures(Fig.8).The theoretical calculation results indicate that the equilibrium isotope fractionation factors between solid phases and[Zn(H2O)6]2+⋅24H2O are much larger than the factors between solid phases and[ZnCl4]2-⋅24H2O.In general,solutions enrich heavy Zn isotopes relative to solid phases except for isotope fractionation between sphalerite and[ZnCl4]2-⋅24H2O.

4 Conclusions

If using gaseous ZnCl2as the Zn species during vaporization,a net Zn isotope fractionation can be deduced based on our calculation results of anorthite,forsterite,and enstatite.The calculated net Zn isotope fractionation of vaporization was about 7–7.5‰.Our theoretical calculation results show that equilibrium isotope fractionation factors could play a small role in isotope fractionation of evaporation processes.The magnitude of Zn isotope fractionation matches the experimental observations of the range of Zn isotope distribution of lunar samples(e.g.,Paniello et al.2012).Therefore,vaporization processes may be the cause of the large distribution of Zn isotope signals found on the Moon.

Furthermore,equilibrium Zn isotope fractionation between smithsonite and sphalerite were about 0.37–0.24‰ in the temperature range of 100–200 °C in good agreement with experimental data.

AcknowledgementsY.L.and co-author are grateful for support from 973 Program Fund(No.2014CB440904),Chinese National Science Fund Projects(Nos.41530210,41490635,41403051).