星型空压机曲柄连杆机构动力学特性分析

李超博，楼京俊，吴海平，石迎潮

1海军工程大学动力工程学院，湖北武汉 430033

2海军工程大学舰船与海洋学院，湖北武汉 430033

3海军潜艇学院动力操纵系，山东青岛 266042

0 引 言

空压机作为生产压缩空气的动力机械，是现代舰船气动系统的“心脏”。高压空气主要用于启动柴油机和倒车、发射雷弹、吹除压载水舱、加强海损邻舱等，还用于气动操纵通海阀和通气阀，接通和断开气动工具、操纵火炮等。目前，主流的大、中型空压机类型有往复式、离心式和螺杆式，对于需要超高压空气的场合，往复式空压机具有一定的优势［1］。

对曲柄连杆机构而言，往复式空压机在运转过程中，主要有压缩气体产生的气体力、机构运动过程中产生的惯性力和力矩、运动副处的摩擦力。通过合理配置空压机列的结构、优化平衡铁配重或添加合理的支撑，可在一定程度上平衡惯性力和力矩。马瑞红等［2］对全平衡式空压机进行了研究，得出该型空压机能够完全平衡惯性力，但惯性力矩无法完全平衡的结论。宋忠尚［3］对PY40V2型空压机平衡重的重量和尺寸进行了设计，并对其振动噪声性能进行了预测。刘成武［4］对大型往复式压缩机的动力学特性进行了分析，重点分析了曲轴的强迫振动特性，并结合边界元和有限元的方法，建立了整机噪声预测模型。为使动力学模型更加准确，黄华军等［5-8］对运动副进行了建模分析，考虑轴承弹性、阻尼、油膜、接触碰撞等因素，获得了相对精确的结果。压缩机的结构形式直接影响曲轴的动平衡，大型往复式压缩机多采用卧式曲轴，类似星型立式曲轴的压缩机比较少见，相关的理论研究还处于起步阶段。曲柄连杆机构的动平衡对压缩机减振设计尤为重要，运动副的运转情况更是直接影响整机振动。

本文将以某型星型空压机曲柄连杆机构为研究对象，对比分析3种结构形式星型连接方式惯性力和力矩的特点。根据空压机压缩气体的相关规律，运用解析的方法推导活塞受力情况。在ADAMS软件中建立虚拟样机，分析平衡铁对动平衡的影响和惯性力的自平衡情况，然后将活塞受力的Matlab数据，构造SPLINE曲线加载到活塞质心，采用柔性化曲轴，并嵌入间隙运动副动力学模型，分析间隙运动副模型的添加对主轴承支反力的影响。

1 空压机结构形式

图1所示为曲柄连杆机构示意图。对于四级压缩的压缩机，传统的曲柄连杆组成形式如图1（a）～图1（b）所示，本文研究的压缩机结合了两者的特点，其组成形式如图1（c）所示，其中1～4表示活塞销的位置。将3种方案的惯性力和力矩进行对比，结果如表1所示［1］。表中：mr为旋转不平衡质量；ms为往复运动质量；r为曲柄半径；ω为曲轴旋转角速度；θ为曲柄转角；λ为曲柄连杆长度比；a2，a3分别为方案2和方案3相邻两列连杆的轴向距离，在进行方案对比时暂且认为它们取值相等。从表中可以看出，方案1主要存在惯性力，方案2和方案3主要存在惯性力矩。相对于方案2而言，方案3的各列曲柄间距进一步缩小，能更大限度地减小惯性力矩。

图1 曲柄连杆机构示意图Fig.1 Schematic diagram of crank connecting rod mechanism

表1 不同方案惯性力和力矩Table 1 Inertial forces and moments of different schemes

2 活塞受力

空压机气体力的计算最早是采用图解的方法，Matlab作为一个强大的数据处理软件，通过解析的方法计算气体力显得更加方便。空压机一个工作循环包括压缩、排气、膨胀和吸气，P1～P4分别表示各个阶段对应的气体力，对应的曲柄转角分别为 0°～27°，27°～180°，180°～295°，295°～360°，满足如下关系式［1］：

式中：S为活塞总行程；Sx为活塞实际行程；Sc为余隙容积；Ps，Pd分别为吸、排气公称压力；Ps′，Pd′分别为考虑压力损失后的实际吸、排气压力；λp为压力系数；A为气缸横截面积；k为绝热系数；m为多变系数。

轴侧气体实际上为大气压力，摩擦力f0一直与活塞的运动方向相反，前180°与气体力的方向相同，后180°与气体力的方向相反，用Nid表示指示功率，则

式中：Vt为活塞的行程容积；λv为容积系数；ηm为机械效率；εs为公称吸气状态下气体的压缩性系数；εd为公称排气状态下气体的压缩性系数；ε为压比。

查阅相关标准，取λp=0.95，k=1.4，m=1.4，ηm=0.92，εs=εd，ε=4.325。由以上公式，计算得到动力计算图（图2）。在虚拟样机中赋予质量属性后，可自动计算惯性力。不考虑惯性力，得到综合活塞力（图3）。各级气缸的气体压强不同，通过设计活塞头面积，使得各级压力尽量相等。

3 曲柄连杆虚拟样机

3.1 建立模型

该型空压机曲柄连杆机构共有113个零件，将其简化为4连杆、4活塞和1曲轴，共计9个零部件。用CATIA建立三维装配体模型，模型保存为stp格式文件后，导入SOLIDWORKS另存为*.x_t格式文件，从而得到Parasolid实体。将实体导入ADAMS/View中，不同部件之间用移动副和转动副相连接，平衡铁与曲轴固定，曲轴转速为1 480 r/min，添加相应驱动，得到ADAMS虚拟样机如图4所示［9-11］。其中，活塞质量定义为相等，均为5 kg，连杆和曲轴都是赋予ADAMS中steel材料属性得到，一、二级连杆质量均为3.96 kg，三、四级连杆质量均为3.98 kg，曲轴质量为33 kg。

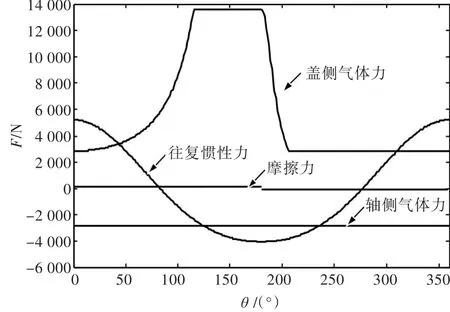
图2 活塞动力计算图Fig.2 Piston power calculation drawing

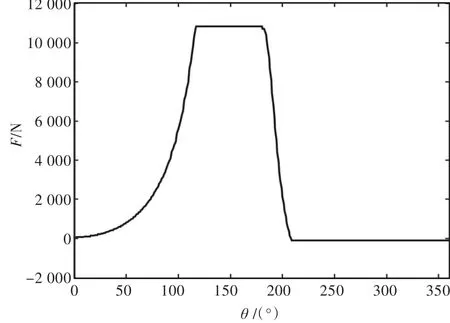
图3 综合活塞力图Fig.3 Synthetic piston force

图4 ADAMS虚拟样机模型Fig.4 ADAMS virtual prototype model

3.2 动平衡

空压机曲轴所受惯性力分为旋转惯性力和往复惯性力，其中旋转惯性力不存在高阶的情况。由于连杆的往复运动和回转运动同时存在，因而产生了高阶往复惯性力。把各部件设定为刚性体，并假定平衡铁的位置和形状不变，质量可变。考虑到结构的对称性，把主轴承x方向受力的Fx作为其所受合力进行研究。

通过虚拟样机仿真，可得到主轴承x方向受力幅值与平衡质量m的关系（图5）。从图中可以看出，平衡铁存在一个最优质量，在设计阶段，应该尽可能去接近这个平衡质量。在平衡铁取得最优质量的情况下，得到主轴承x方向受力频域图（图6）。虽然理论上该型空压机的惯性力为0，但在工程实际中，不能保证活塞质量和连杆质量完全相等，三、四级连杆要比一、二级连杆厚0.5 mm，因而会出现惯性力不平衡的情况。该型空压机的惯性力主要集中在前三阶，四阶及以上可忽略不计。由于活塞圆周布置对二阶惯性力有着良好的自平衡能力，所以动平衡应主要考虑一阶和三阶惯性力。

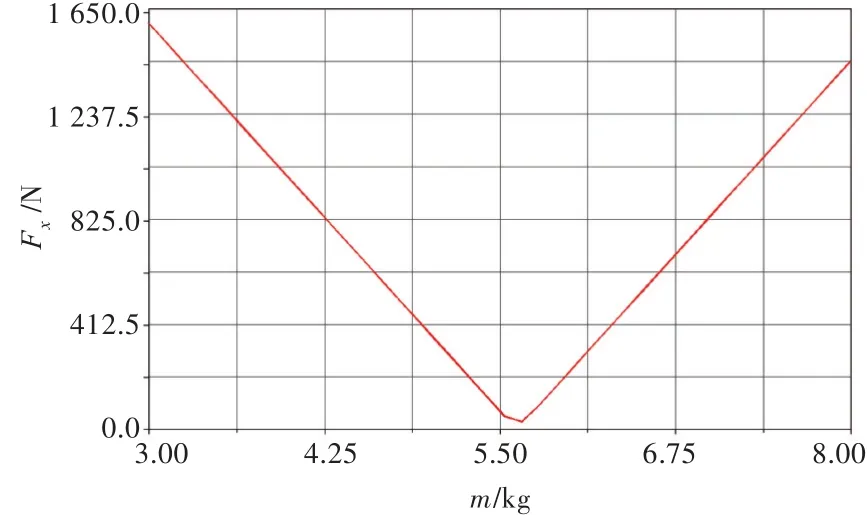
图5 主轴承受力幅值与平衡质量的关系Fig.5 Relationship between main-bearing stress amplitude and equilibrium mass

图6 曲轴旋转副受力频域图Fig.6 Frequency domain stress diagram of crankshaft revolution joint

3.3 柔性化

将图3得到的综合活塞力在ADAMS软件中构造SPLINE曲线，加载到活塞质心，方向沿气体膨胀时活塞的运动方向。采用四面体单元将曲轴和连杆柔性化，曲轴划分为3 574个单元，一、二级连杆划分为980个单元，三、四级连杆划分为1 056个单元。单独将4根连杆柔性化，得到如图7所示受力图；单独将曲轴柔性化，得到如图8所示受力图。从2幅图中可以看出，连杆柔性化时，主轴承的受力基本没有变化，曲轴柔性化时，主轴承的受力发生了一定程度的变化，这说明曲轴比连杆更趋近于柔性体。在运动的初始阶段，柔性体力的传递有一个过程，驱动带动的运动需要经过短时加速阶段，所以初期主轴承的受力较大。而刚性体则认为力和位移都是瞬时传递的，从运动开始便进入稳态。

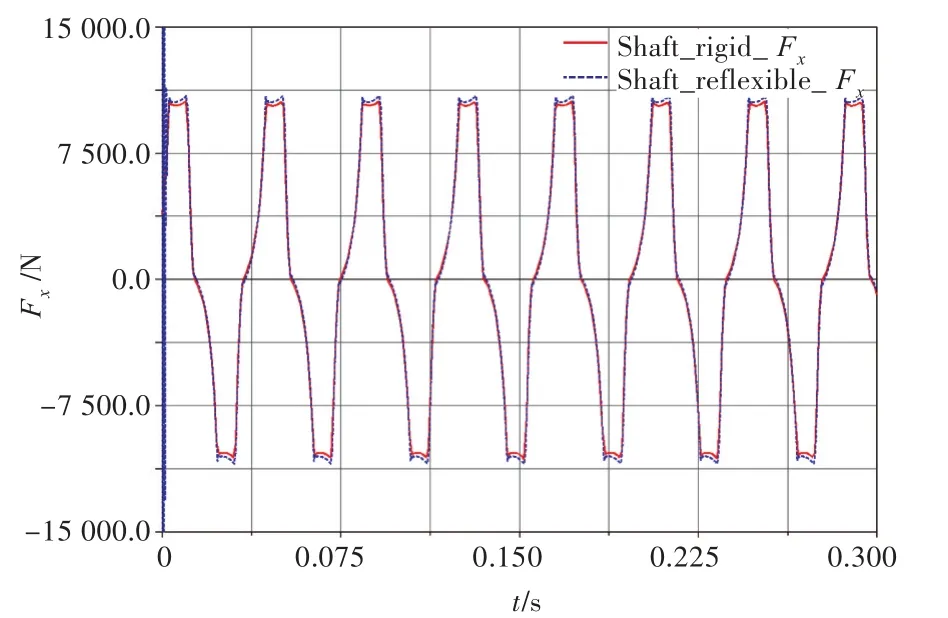
图7 连杆柔性化前、后主轴承受力Fig.7 Main bearing force before and after connecting rod flexibility

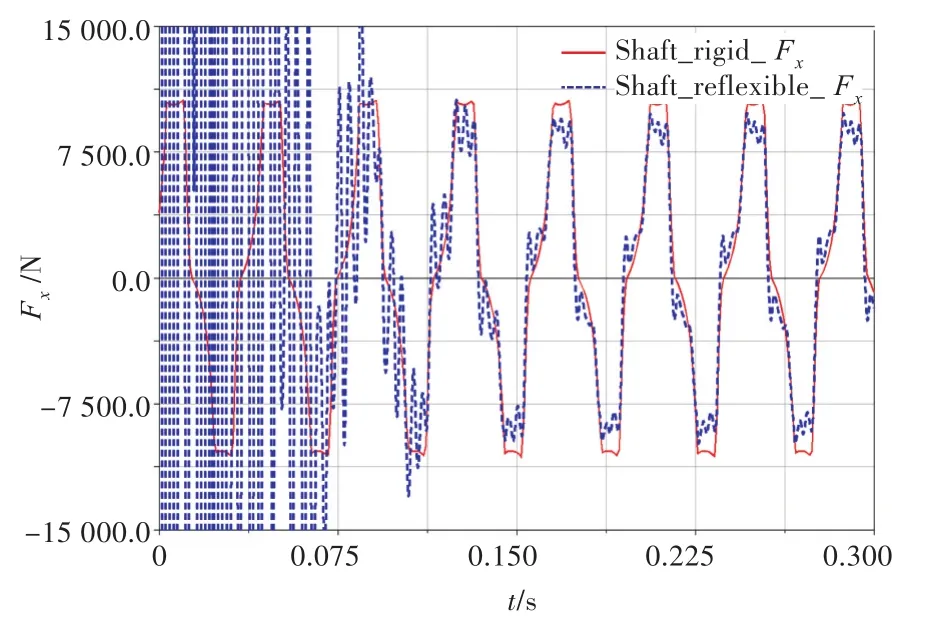
图8 曲轴柔性化前、后主轴承受力Fig.8 Main bearing force before and after crankshaft flexiblility

4 含运动副间隙动力学模型

由于制造、装配误差和磨损，运动副间隙总是存在。间隙会引起运动副关节存在脱离接触的情况，等到再次接触时会触发碰撞，引起冲击载荷，并有可能造成运动副磨损加剧或破坏失效。ADAMS软件内置有IMPACT碰撞函数，该函数计算接触力的表达式为［12］

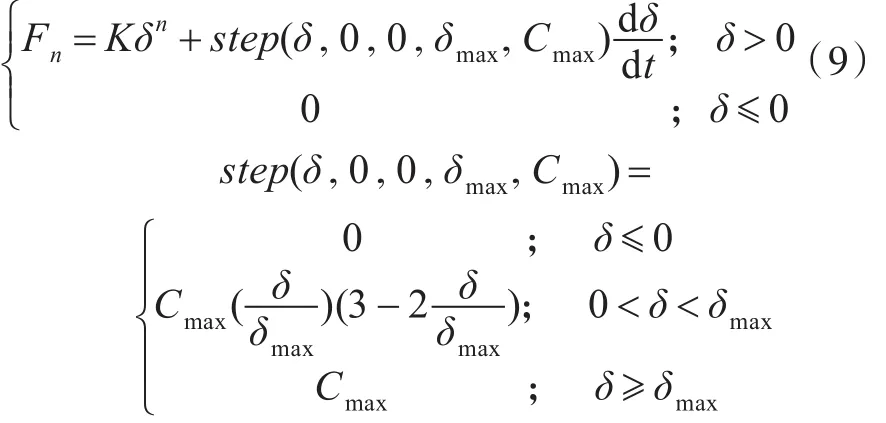
式中：K为碰撞刚度；δ为运动副接触面的穿透深度；为碰撞的相对速度；n为碰撞力指数；C为阻尼系数。

在建立运动副碰撞间隙的同时，考虑摩擦作用，将COULOMB摩擦模型嵌入到ADAMS分析软件中，以更加全面地研究运动副间隙对主轴承支反力的影响［13］。本文仅在曲柄销和4个连杆大端之间添加了间隙模型，仿真参数设计如表2所示。

表2 仿真计算参数Table 2 Simulation parameters

图9为无摩擦间隙转动副模型主轴承受力频域图。由图可见，前3阶惯性力依然比较明显，间隙模型使得主轴承在200～400 Hz处出现宽频带激励力。图10为有摩擦间隙转动副模型主轴承受力频域图。对比图9可以发现，225 Hz处及之后的2个频谱峰值都有所下降，除转频及其倍频外，其他频率下的频谱峰值都是由于间隙及摩擦的存在而产生，激振频带明显比无摩擦时要宽。

为验证计算的真实性，通过实验进行验证。将空压机4个机脚（1#～4#）通过搭载隔振器与基座相连接，采集4个机脚的垂向振动加速度a，得到空压机机脚加速度频谱如图11所示。从图中可以看出，在200～400 Hz频段处出现了振动加强的情况，这与仿真得到的主轴承受力在该频段内出现增强的情况相符。

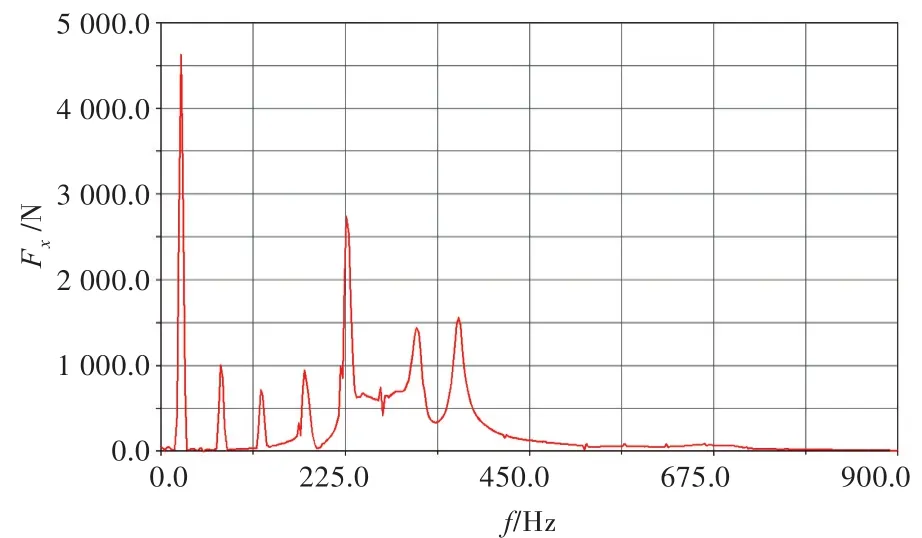
图9 无摩擦间隙转动副模型主轴承受力Fig.9 Main bearing force of revolute joints clearance model without friction

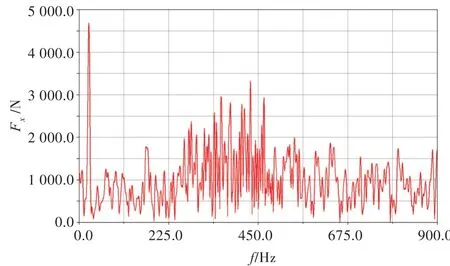
图10 有摩擦间隙转动副模型主轴承受力Fig.10 Main bearing force of revolute joints clearance model with friction

图11 实测空压机机脚振动加速度Fig.11 Foot vibration acceleration of air compressor measurement

5 结 论

本文以星型空压机曲柄连杆机构为研究对象，考虑气体力和运动副间隙，建立了虚拟样机，通过动力学仿真，可得到如下结论：

1）该型空压机相对于传统结构形式的星型压缩机能够更好地平衡惯性力，并最大程度的减小惯性力矩；尤其对于二阶惯性力，该机构具有良好的自平衡能力，动平衡设计主要考虑一阶和三阶惯性力即可。

2）考虑柔性效应的动力学模型更接近空压机的实际工作情况，对该机型而言，连杆的柔性化对主轴承受力的影响可以忽略不计，曲轴柔性化对主轴承受力有一定的影响。

3）间隙摩擦的存在对主轴承受力的影响较大，通过合理设置接触模型的相关参数，可以得出中、高频的振动能量极有可能是由运动副的相互作用产生。通过实测4个机脚的振动数据，在一定程度上验证了所建动力学模型的正确性。