基于改进禁忌搜索算法的舰载机保障作业调度
2018-10-25李梦龙余明晖
李梦龙,余明晖
华中科技大学自动化学院,湖北武汉430074
0 引 言
舰载机作为舰空母舰(简称“航母”)的核心作战装备,对其综合作战能力的影响很大[1],且舰载机的出动能力是判断航母综合作战能力的关键指标[2]。因此,航母的总体设计始终围绕着如何有效提高舰载机的出动能力这一战技指标而展开[3]。当舰载机通过弹射器起飞执行任务之前,必须严格按照预先制定的甲板作业流程进行舰面保障[4],故舰载机的出动能力与航母甲板上的保障作业调度策略密切相关。航母甲板上的有限保障资源、多变作业环境和复杂作业流程等决定了舰载机保障作业调度是制约舰载机出动能力的关键因素[5]。
舰载机的保障作业调度问题,即是在有限的甲板空间和保障资源等约束条件下,为舰载机提供合理的保障站位和保障次序,以缩短舰载机的牵引距离并减少保障作业总时间,从而确保在舰载机起飞之前完成保障任务,这实际上属于资源约束的优化调度问题[5]。
目前,国内外学者针对航母甲板保障作业调度问题开展了广泛的研究。例如,美国麻省理工学院计算机科学与人工智能实验室开发了可以人机交互的航母甲板作业规划决策支持系统(Deck Course of Action Planner,DCAP),可用于对舰载机保障作业调度进行智能决策[6];Dastidar等[7]提出了基于排队网络的分布式策略,可用于解决航母甲板的调度问题;韩庆田等[8]运用遗传算法来解决舰载机的保障作业问题,直观地提出了舰载机的保障流程方案;司维超等[9]建立了舰载机出动调度的基础模型,并利用融合了多种群和混沌局部搜索后改进的粒子群算法对调度问题进行了求解;韩维等[10]建立了多目标的多机一体化机务保障模型,提出了一种自适应混合差分进化算法,可以提高多目标舰载机的机务保障效率。
目前,国内外主要采用计算仿真方法和智能优化算法来求解舰载机的保障作业调度问题。其中,计算仿真方法一般通过逻辑关系和参数选择来构建模型,但不同的系统模型会导致不同的结论;智能优化算法的计算速度较快,能够和其他算法相结合,和仿真方法相比更具优势。同时,现有的研究工作主要集中在舰载机的保障站位分配上,鲜有针对资源冲突时保障次序调度方面的研究,也没有考虑到各架次舰载机的起飞时间对保障计划的影响。本文将综合考虑舰载机保障作业、起飞时间和转运时间等因素,对保障次序进行调度优化,用以在较短的计算时间内求解可行的调度方案。鉴于舰载机保障作业调度和车间作业调度非常相似,拟将舰载机保障作业调度问题转换成车间作业调度问题,并通过智能优化算法对其进行求解,从而提出一种效率更高的基于禁忌搜索的改进算法。
1 模型描述与转换
1.1 舰载机保障作业调度问题
本文将以“尼米兹”级航母的传统多站式保障作为参考,并对其进行适当的简化处理,即不考虑保障作业时的干扰因素和多个波次之间的影响,并假设各架舰载机完成保障作业的站位和次序已提前由调度人员制定完毕。
假设在一个波次中有2架舰载机(设为F1和F2)需起飞执行任务,该波次的起飞时间为8:00,起飞时间间隔为10 min(即F1的起飞时间不应晚于8:00,F2的起飞时间不应晚于8:10),且在起飞之前需要完成补充燃料/滑油/特种液体和气体、充电、挂载弹药等保障任务[11]。执行保障任务分串行和并行2种关系:串行指多个保障任务只能依次完成,总的完成时间等于单个保障任务完成时间之和;并行指多个保障任务可以同时进行,总的完成时间等于单个保障任务完成时间的最大值。由于真实的保障作业完成时间会在某个范围内动态变化,并具有一定的随机性,故本文仅考虑时间波动区间较小的情况,并取近似值作为保障完成时间。假设2架舰载机的保障任务分别在5个站位(A1,A2,A3,A4,A5)上完成,每个站位可以提供若干项保障服务,但在同一时间只能给1架舰载机提供保障。假设调度流程为:F1依次到A1,A2,A4站位完成保障服务;F2依次到 A3,A2,A5站位完成保障服务。每架舰载机完成保障作业的次序、站位、任务及时间如表1所示。当舰载机在一个站位上完成保障作业之后,就会被牵引到下一个保障站位,故牵引的转运时间和牵引距离成正比。本文忽略舰载机的弹射起飞时间,故其保障作业完成时间即起飞时间。
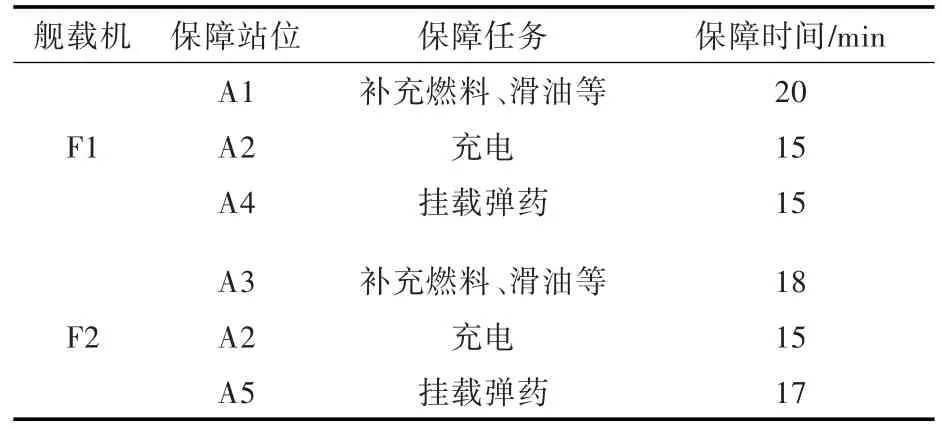
表1 舰载机的保障作业Table 1 Support operation of carrier-based aircraft
由于每个站位在同一时间只能给1架舰载机提供保障服务,当2架舰载机需要在5个站位上完成各自的保障作业时,如果不进行调度,就有可能出现2架舰载机同时在同一个站位上进行保障作业的问题,如图1所示的A2站位阴影段。为了解决站位冲突问题,必须使保障作业总时间尽可能短,并且需同时满足以下条件:
1)每架舰载机需按照预先设定的保障作业次序,依次到每个站位上完成保障作业。
2)单个站位在同一时刻只能服务1架舰载机,且单架舰载机在同一时刻只能在1个站位上进行保障。
3)每架舰载机必须在起飞之前完成所有的保障作业。

图1 不可行解Fig.1 Infeasible schedule
1.2 车间作业调度问题
车间作业调度问题(Job-shop Scheduling Problem,JSP)是一个经典的生产调度问题,也是一个典型的NP-hard问题,其中NP是指非确定性多项式(Non-deterministic Polynomial,NP)。该问题起源于加工制造行业,目前在交通运输、网络通信等领域也得到了广泛应用。车间作业调度问题可以描述为:给定若干个工件和若干台机器,每个工件按照预先设定的加工工艺路线,依次到各台机器上完成加工任务。由于每台机器上都会有若干个工件需要加工,故调度方案需要确定各台机器的工件加工次序,以使最大完工时间(Makes⁃pan)最短。
车间作业调度问题的目标函数为

车间作业调度问题的约束条件为:

式(1)~式(4)中:tn为最大完工时间;ti和tj分别为工序i和工序j的开始时间;O={0,1,…,n},为工序i和工序j的集合,其中0和n为虚拟工序,工序0为起点,工序n为终点;D={d1,d2,…,dn},为各工序的加工时间集合,其中(di,dj)∈D;A为工件本身工艺路线决定的加工次序的约束集;Ek为在机器k上进行加工的约束集;M={1,2,…,m}为机器集合。
式(1)表示调度目标为令最大完工时间最小化,式(2)表示工序的开始时间必须大于0,式(3)表示一个工件必须按照工艺路线依次加工,式(4)表示一台机器在同一时间只能加工1个工件。
1.3 2个模型之间的差异及转换
由上文可知,舰载机保障作业调度问题与车间作业调度问题非常相似,但这2个模型之间有2个不同点:
1)在车间作业调度问题中,每个工件都是从固定起始点出发,按照加工次序在不同机器上加工并到达终点,因此在不同的调度方案中,每个工件完成所有工序到达终点的时间各不相同;而在舰载机保障作业调度问题中,每架舰载机的起飞时间不同,且每架舰载机必须在起飞时间之前完成所有的保障作业。简单而言,车间作业调度问题可以视为从固定起点到非固定终点的排序,而舰载机保障作业调度问题则将起飞时间视为固定终点,如果将其单纯地转换为车间作业调度问题,很可能得不到有效解。
2)在车间作业调度问题模型中,没有考虑一个工件完成一项工序后,从上一台机器移动到下一台机器的运输时间;而在舰载机保障作业调度问题中,转运时间对最终调度方案的影响不容忽视,所以在调度过程中应考虑转运时间。
基于此,本文处理如下:将舰载机保障次序的约束逆向转换为车间作业调度中工件的加工次序约束,每项保障作业与加工工序逆序对应;将舰载机集合转换为车间作业调度中的工件集合;在每个工件的第1项工序前插入一项虚拟工序,即取所有舰载机中最晚的起飞时间与该工件所代表的舰载机的起飞时间相减,差值作为该虚拟工序的加工时间(如果差值为0,则不插入虚拟工序);在剩余相邻工序之间插入一项虚拟工序,将舰载机转运时间作为该工序的加工时间。
按照以上处理步骤,图1即可转换为图2。图2中:JOB1对应 F1,JOB2对应F2;M1,M2,M3,M4,M5分别对应A1,A2,A3,A4,A5,其中非灰色工序的加工时间与舰载机保障作业的时间相同;灰色节点为插入的虚拟工序,其加工机器为M0,M0是一台可以在同一时间加工无限工件的特殊机器;JOB1中第1个灰色工序的加工时间为F2与F1起飞时间的差值,其他灰色工序的加工时间为相邻站位之间的转运时间。
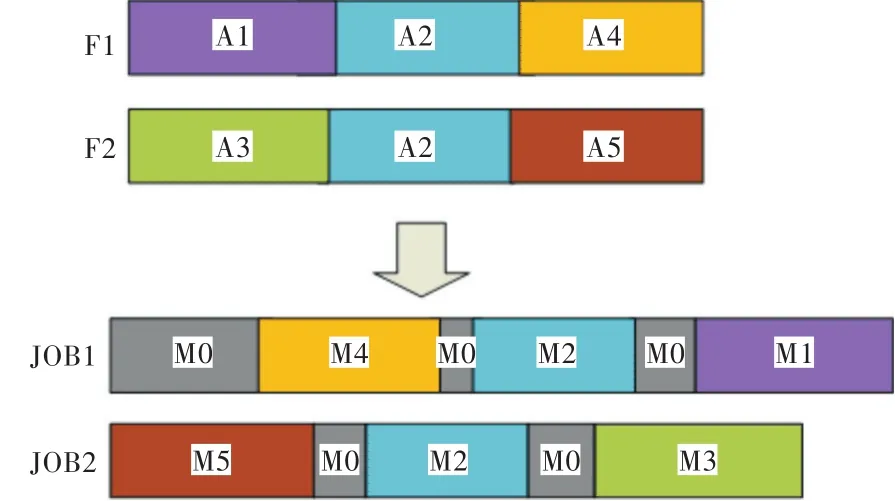
图2 模型转换Fig.2 Model transformation
2 求解算法
车间作业调度问题的求解方法主要可以分为最优化算法和和启发式算法2种。其中最优化算法(例如,分支定界法)的计算量非常大,难以应用于航母甲板环境。而启发式算法中:模拟退火算法的收敛速度过慢,搜索空间过于庞大,且温度难以掌控;遗传算法则有早熟和效率低下的问题;禁忌搜索(Tabu Search,TS)算法在解决了初始解、搜索策略和禁忌列表长度等问题之后,其计算效率在可接受范围内。故本文将以禁忌搜索算法为基础,提出一种改进启发式算法,用以求解舰载机的保障作业调度问题。
禁忌搜索算法采用局部邻域搜索的思想,在全局逐步寻优,其搜索过程如图3所示。禁忌搜索的主要思想是对初始解的邻域进行搜索,并找到候选解作为当前解,采用禁忌列表存储已搜索过的区域信息,从而在之后的迭代搜索中避免回到原先已搜索过的区域。禁忌搜索算法主要有6个基本要素:初始解和目标函数、邻域结构、候选解、禁忌列表及长度、藐视准则、终止规则[12]。本文提出的改进禁忌搜索算法(Improved Tabu Search,ITS)将主要围绕禁忌列表的长度、产生初始解、加入分散搜索策略和集中搜索策略等开展工作。
1)禁忌列表。禁忌列表用于存储被禁忌的对象,以防止重复搜索之前已搜索过的区域。如果禁忌列表的长度过长,搜索将被抑制;如果长度过短,则将导致重复搜索并进入循环[13]。改进的禁忌搜索算法将采用动态的禁忌列表长度L,其值将在Lmin和Lmax这2个极限值之间动态变化,具体如下:
(1)如果找到比当前解更优的解,将L-1作为禁忌列表的长度,并保持L≥Lmin。
(2)如果没有找到比当前解更优的解,将L+1作为禁忌列表的长度,并保持L≤Lmax。

图3 禁忌搜索流程Fig.3 Tabu search process
(3)假设禁忌列表长度L的初始值为Lmin,其中Lmin=2w/3,Lmax=2w,w为加工车间的工件数量。
2)产生初始解。在禁忌搜索之前必须给定一个初始解,而一个好的初始解可以显著提升禁忌搜索算法的性能[12]。考虑到移动瓶颈法不仅可以快速求解车间作业问题,而且其得出的解比SPT和FCFS等优先分配准则的解更加优秀,所以本文将采用移动瓶颈法为禁忌搜索提供初始解。移动瓶颈算法是一种启发式算法,通过在所有机器中找到最大延迟的瓶颈机器,然后对其进行单机调度,调度完成后再对剩余机器重复以上步骤。
3)分散搜索策略。分散搜索策略可以对解集的区域进行广泛搜索,以避免陷入局部搜索。如果在某个区域一直没有找到比当前最优解更好的解,则将重新在新的区域开始搜索。如果在某次搜索中一直没有找到比当前调度方案的最大完工时间更短的方案,则应记录其迭代搜索次数,当该次数达到预先设定的上限时,就找到一个新的解作为下一次迭代的初始解,然后清空禁忌列表。
4)集中搜索策略。当最优解被更新时,如果进一步搜索当前区域,则有可能找到更多的最优解。如果在局部区域中发现了比当前最优解更好的解,应将最优解更新并清空禁忌列表,用以使当前区域的后期搜索更加自由。
在将舰载机保障作业调度问题转换为车间作业调度问题的过程中,本文引入了1台虚拟机器M0。由于M0的容量无限大,允许在同一时间加工无限工件,故M0的工件加工次序将不影响总的加工时间。因此,在改进禁忌搜索算法中将不调换M0上的工件加工次序,以节省计算时间。
3 实验仿真结果
为了验证本文算法的改进效果,参考“尼米兹”级航母在1997年的“高潮演习”资料和相关文献[14-15],设计了2个实例。实例1中舰载机保障作业的站位和时间如表2所示,舰载机到下一个站位的转运时间与站位之间的距离成正比。假设在某个波次需要出动6架舰载机(F1~F6),每架舰载机起飞前必须完成加油、飞行准备、充电、挂弹这4项保障任务,每项保障作业均有2个保障站位(Y1/Y2,P1/P2,S1/S2,G1/G2)提供服务。该波次的起飞时间起点为10:35,起飞间隔为5 min。

表2 舰载机保障作业次序(实例1)Table 2 Deck operation(case 1)
本实验平台采用Java语言开发,运行的机器环境为Core i5-6200U,CPU主频为2.3 GHz,内存为8 GB,操作系统为Windows 10。由于禁忌搜索算法对初始解的依赖程度较高,为了验证移动瓶颈算法对禁忌搜索效率的改进效果,将以改进的禁忌搜索算法为基础,分别采用随机解(ITS-R)、FCFS规则产生的解(ITS-FCFS)和移动瓶颈算法产生的解(ITS-M)作为初始解来进行计算对比。禁忌搜索算法的终止规则为:当前最优解的更新次数不超过60次。表3所示为10次重复独立计算的对比结果,其中:ITS-R对应的最优解平均值为110,计算时间平均值为0.964 s;ITS-FCFS对应的最优解平均值为110,计算时间平均值为0.825 s;ITS-M对应的最优解平均值为110,计算时间平均值为0.682 s。
由表3可知,虽然3种初始解对应的最优解相同,但采用移动瓶颈算法产生初始解的计算效率最高。因此,移动瓶颈算法产生的初始解可以有效改进禁忌搜索算法,其甘特图如图4所示。图中灰色部分表示舰载机从上一个站位到下一个站位的转运过程。改进算法求解的保障作业方案总时间为110 min,整个保障作业流程从9:10(F2加油)一直持续到11:00(F6起飞)。

表3 不同初始解的计算结果对比Table 3 Comparison of calculation results of different initial solutions
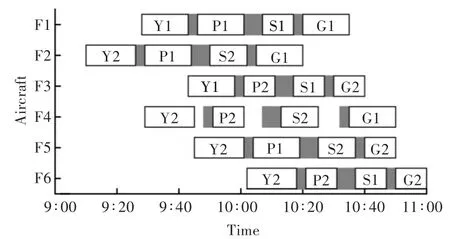
图4 实例1的甘特图Fig.4 Gantt chart of case 1
为了对比ITS算法和传统TS算法的计算效率,分别采用这2种算法对实例1进行了10次重复独立计算,其对比结果如表4。由表4可知:ITS算法对应的最优解平均值为110,计算时间平均值为0.682 s;TS算法对应的最优解平均值为110.1,计算时间平均值为1.029 s。因此,ITS算法的计算速度比TS算法更快,且TS算法偶尔无法找到最优解110。
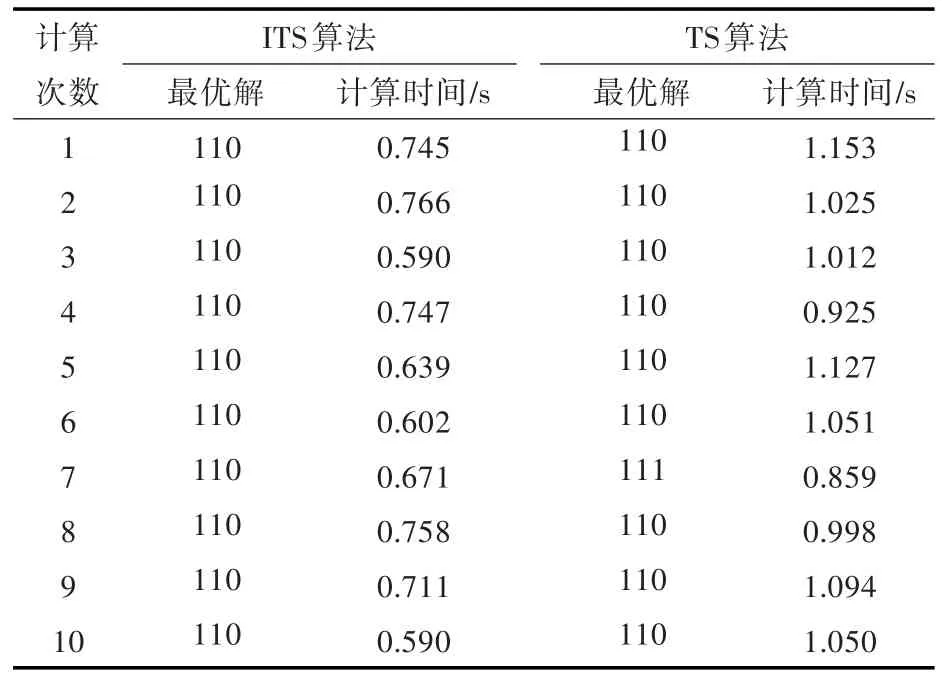
表4 ITS算法和TS算法的对比(实例1)Table 4 Comparison between ITS algorithm and TSalgorithm(case 1)
为进一步验证不同数量舰载机出动情况下的计算性能,本文还设计了实例2。假设出动10架舰载机,起飞时间为10:42,起飞间隔为2 min,保障作业安排如表5所示。

表5 舰载机保障作业次序(实例2)Table 5 Deck operation(case 2)
针对实例2,ITS算法和传统TS算法的计算性能对比如表6所示。其中:ITS算法对应的最优解平均值为145,计算时间平均值为3.73 s;TS算法对应的最优解平均值为146.6,计算时间平均值为4.613 s。因此,ITS算法的计算效率和优化效果均优于TS算法。
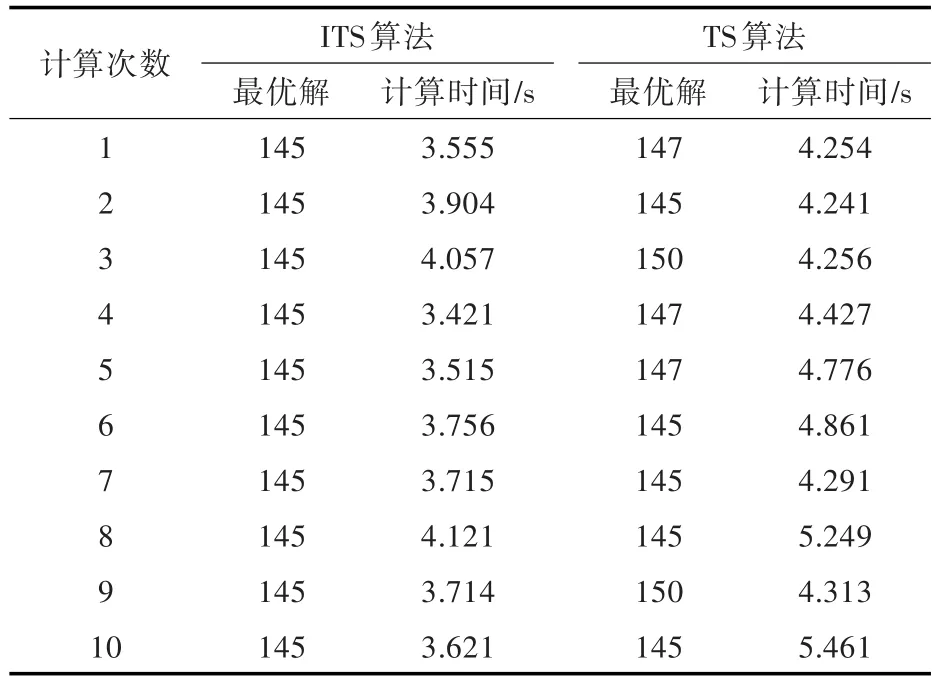
表6 ITS算法和TS算法的对比(实例2)Table 6 Comparison between ITS algorithm and TSalgorithm(case 2)
4 结 语
本文将舰载机保障作业调度问题转换成车间作业调度问题,建立了保障作业调度模型,并提出了一种改进的禁忌搜索算法对该模型进行求解。相对于传统禁忌搜索算法,改进算法采用了移动
瓶颈算法得出初始解,增加了分散搜索策略和集中搜索策略,并使禁忌列表的长度随搜索进行动态变化。不同规模的实例验证计算结果表明,改进的禁忌搜索算法能够有效优化舰载机的保障作业流程,并且其优化结果和计算速度均优于传统的禁忌搜索算法。
