基于优势度测量的舰船电子信息系统方案优选

曲全福，李金鹏

1海军驻大连船舶重工集团有限公司军事代表室，辽宁大连116005

2中国舰船研究设计中心，湖北武汉430064

0 引 言

舰船电子信息系统是指在高技术局部战争环境中，为舰艇联合作战提供情报、监视、侦察、指挥、控制、通信、导航、定位和电子战等功能的系统［1-2］。对舰船电子信息系统方案进行论证和选择时，由于数据缺乏、未来技术发展情况未知、决策成员自身的信息判断和处理能力有限等影响，决策人员往往难以提供决策参数的准确值，一般只能提供不完全信息。同时，选择舰船电子信息系统方案需要综合考虑技术先进性、作战效能、经济性等诸多因素，故单个决策成员难以兼顾考虑，也无法掌握所有的必要信息。因此，为了减少决策失误，往往推荐多人共同研究决策，以综合利用群体成员的知识和经验，从而得到更为合理的决策结果。

基于初始不完全信息，决策成员一般需要多次决策才能解决问题。为此，一些学者将多目标决策领域中的交互式决策思想引入到多属性决策领域，为解决这类问题提供了一条新的途径。Salo等［3］提出了一种集结群决策成员偏好信息的交互式决策方法，通过将决策成员提供的不完全偏好信息转化为对边际效用的约束条件，提出了强优势和弱优势关系；在弱优势情况下，决策成员需根据决策结果提供更多的偏好信息。Kim等［4］针对不完全信息群体决策开展了大量工作，提出了交互式群决策的框架，先后建立了基于偏好强度的群集结模型和基于区间效用值的群集结方法。文献［5-7］研究了不完全信息条件下的多属性决策方法，王凯歌等［8］和赵楠等［9］将模糊集、模糊层次分析等不完全信息综合评价法应用到了舰船系统的综合评估中。

目前，舰船电子信息系统的方案优选一般针对单个决策成员，属性值也多为确定数值。然而，关于从群决策的角度进行舰船电子信息系统方案优选，且方案属性值、属性权重和决策成员权重均为不完全信息的工况，目前尚未开展相关研究工作。本文将针对属性和权重均为不完全信息的舰船电子信息系统方案，从严格优势、弱优势关系出发，研究方案间优劣程度的测量指标，并建立不完全信息情况下方案优势度的计算方法与模型，用以为舰船电子信息系统备选方案的优选提供一种科学的量化方法。

1 不完全信息工况下舰船电子信息系统方案的优选方法

1.1 问题描述

对于不完全信息工况下舰船电子信息系统方案的群体决策问题，假设如下：决策成员集为G={D1，D2，…，DK} ，其中Dk为第 k个决策成员，且k=1，2，…，K；系统方案集为X={x1，x2，…，xm}，其中xj表示第j个方案，且j=1，2，…，m；评价系统方案的属性集为C={c1，c2，…，cn}，其中ci表示第i个属性，且i=1，2，…，n；决策成员Dk的权重为pk，其中且pk＞0；方案评价属性的权重为，其中为决策成员Dk给出的属性ci的权重，满足=1且＞0；D给出的方案x在属性c下的集结效用kji值为，其集合记为决策成员权重集，其中为决策成员Dk权重的不完全信息集；记W为权重不完全信息集，记为决策成员k的方案偏好值集，其中φkw为决策成员Dk给出的属性权重的不完全信息集；V为方案效用值不完全信息集，vk为成员Dk给出的方案属性值的不完全信息集。

1.2 方案优选决策方法

1.2.1 优势关系与优势度计算

决策成员Dk关于系统方案xj的效用值为

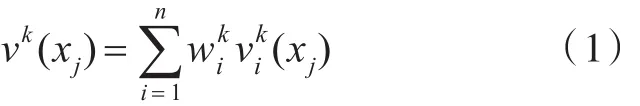
在不完全信息集内，通过求解线性规划模型，即可得到个体集结效用值的取值范围：

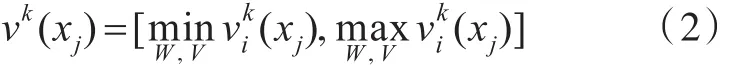
决策成员集G关于方案xj的集结效用值为

根据多属性评价理论，如果方案xj的群体集结评价值满足式（1），则可将xj视为系统方案集X内的群体最优方案，即

式中，l=1，2，…，m且l≠j。

然而，在由属性权重不完全信息集W、方案效用值不完全信息集V和决策成员权重信息集P构成的可行域空间内，判断方案xj是否满足式（1）较为困难。但可以通过方案成对比较，来确定不完全信息工况下方案的优势关系。

定义1：若，则表示方案xj相对方案xl呈群体绝对优势，记为xjGADxl。

其中：

定义 2：若，且至少存在 一个使成立，则称方案xj相对方案xl呈群体严格优势［10］，记做xjGSDxl。

其中：

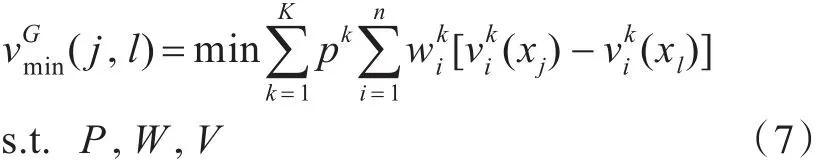
定义 3：若或，则称方案x相对方案x呈群体弱优势，jl记做xjGWDxl。

其中：

通过系统方案的群体优势关系，可以确定最优的舰船电子信息系统方案或所有方案排序。但是，在实际方案优选过程中，对其他任意方案而言，往往不存在呈群体绝对优势或严格优势的方案。因此，需要一种评判标准来实现备选方案集的全序关系。假设决策成员Dk关于各个方案的优势度指标为，其值越大，方案越优。

其中：

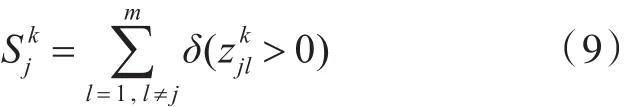
将参与择优的成员群体偏好信息进行集结，然后通过求解数学规划模型来确定成对方案的群体优势关系。同时，集结各决策成员关于方案的优势度可以得到方案群体的优势度指标，其表达式为

若群体成员的权重信息不完整，则式（11）可以转化为如下规划模型：

基于方案群体优势关系和优势度指标，即可确定备选方案集的全序关系，但是决策成员并不一定对这一决策结果满意或能够达成一致意见。

1.2.2 群体一致性判定

在实际决策过程中，依据不完全初始信息得出的决策结果往往难以让所有决策成员满意，故需要进行信息交互以获取支撑一致性决策的更多信息。同时，由于每个决策成员对备选方案的偏好不同，故最终的决策结果无法与每个决策成员的意见保持一致，这将造成决策难以完成。因此，需要一种标准来评判最终结果能否被所有决策成员接受，本文将借鉴引入一种基于群体一致性的指标来作为判定准则。

定义4：关于区间数的一致性，设2个区间数a=[a1，a2]和b=[b1，b2]，定义区间数a和b的一致度函数为，其中|a|和|b|分别为区间数a和b的长度。

一致度函数R(a，b)需满足如下要求：

1）0≤R(a，b)≤1，且R(a，b)越大，区间数a和b的一致程度越高。

2）当且仅当a1=b1且a2=b2时，R(a，b)=1。

定义5：关于方案群体一致性指标，假设不完全信息工况下决策成员Dk关于方案xj的综合效用值为，决策成员集G关于方案xj的综合效用值为则决策成员集G关于方案xj评价值的平均一致性指标为

定义 6：定义，为备选方案集的群体评价平均一致性指标。

根据区间数一致性函数的定义可知：对单个方案xj而言，r(xj)值越大，各决策成员Dk与成员集G决策结果的一致性越高；对备选方案集而言，值越大，各决策成员Dk与成员集G决策结果的一致性越高，即备选方案被所有决策成员接受的可能性越高。因此，指标r(xj)和可以作为交互式决策过程中信息交互的起始或中止的客观判定条件。

1.2.3 模型计算步骤

基于方案群体优势关系和优势度计算，即可完成交互式的不完全信息多属性群决策，具体步骤如下：

步骤1：决策成员提供或更新属性值、属性权重等决策参数的不完全信息。

步骤2：对决策成员提供的决策信息进行一致性检验，若信息不一致，则重复步骤1。

步骤3：根据定义1，2，3，确定群体关于成对方案的绝对优势、严格优势和弱优势关系，若可以实现全部备选方案的择优或排序，则直接转至步骤5，否则进行步骤4。

步骤4：根据式（7）和式（10），计算各备选方案的群体优势度，确定方案的排序。

步骤5：将群体决策结果反馈给各决策成员，若各决策成员对群体决策结果均表示满意，则直接转至步骤7；若有决策成员对结果不满意，则进行步骤6。

步骤6：计算方案群体评价一致性指标r(xj)和方案群体评价平均一致性指标。

步骤7：各备选方案的群体决策结果有效，任务结束。

2 算例分析

假设某舰船电子信息系统方案的论证专家组成员数量为K=3，根据n=3个属性（使用效能c1、全寿期费用c2和技术先进性c3）对m=4个系统备选方案进行评价和选择。

决策成员D1，D2，D3给出的属性效用值不完全信息分别如表1、表2和表3所示。决策成员给出的属性权重的不完全信息如表4所示。

表2 D2给出的属性效用值不完全信息Table 2 Incomplete information of attribute value given by D2

表3 D3给出的属性效用值不完全信息Table 3 Incomplete information of attribute value given by D3

表4 属性权重的不完全信息Table 4 Incomplete information of attribute weight

假设3个决策成员的权重分别为p1=0.3，p2=0.3，p3=0.4，则决策成员一致同意最终决策结果的前提条件为：r(xj)＞0.6且≥0.7。

采用上述方法求解舰船信息系统方案评审委员会对4个备选方案的优劣排序结果，步骤如下：

1）决策成员提供初始不完全信息，按照定义4对初始信息进行一致性检验，可知表1～表4的信息满足一致性。

2）确定不完全信息下的方案群体优势关系和群体优势度。方案群体优势度关系为：vGmin(1，2)=，可知x2GSDx4，x3GSDx4。

然后，计算每个决策成员对4个系统方案的综合评价值，并根据式（11）和式（12）进行方案成对比较，计算各方案的群体优势度，得，则方案排序为x2≻x3≻x1≻x4。将决策结果反馈给决策成员，成员D1对方案1、方案2和方案3间的优劣排序结果不满意，需进行群体决策结果一致性计算。

3）根据式（13），计算各成员群体一致性指标，得r(x1)=0.52，r(x2)=0.64，r(x3)=0.66，r(x4)=0.79，=0.65，可知 r(xj)=0.4＜0.6，=0.65＜0.7，即不满足群体成员对决策结果一致性的要求。因此，需要决策成员通过信息交互来提供新的决策参数信息。

4）决策成员对4个方案属性效用值信息进行修改，决策成员D1删除了，增加了；决 策 成 员 D2将修改为，增加了和；决策成员 D3增加了和。

5）重新按照步骤1）开始，进行信息一致性检验和方案的群体优势关系求解，可知决策成员修改或新提供的决策参数信息与原有信息满足一致性。方案群体优势度关系为：，，可知xGSDx，xGSDx。2434

根据式（11）和式（12）进行方案成对比较，计算各方案的群体优势度，得，，，则方案的排序为x2≻x3≻x1≻x4。将决策结果反馈给群体成员，成员D3对方案2和方案3间的优劣排序结果不满意，需进行群体决策结果一致性计算。

6）根据式（13），计算各成员群体一致性指标，得r(x1)=0.62，r(x2)=0.74，r(x3)=0.72，r(x4)=0.78 ，=0.72 ，可 知r(xj)=0.62＞0.6 ，=0.72＞0.7，满足群体成员对决策结果一致性的要求。

7）根据群体决策结果，系统方案x2为最佳选择，则综合评价排序为：x2≻x3≻x1≻x4。

由此可见，通过群体一致性计算和迭代，最终形成了满足决策群成员一致性要求的优劣排序结果，从而为不完全信息下的方案优选提供了一种有效的量化方法。

3 结 语

本文针对舰船电子信息系统方案优选中的不完全信息多属性决策问题，提出了一种基于优势度测量的不完全信息方案优选方法。首先，构建了不完全信息工况下求解方案群体优势度的非线性优化模型，通过模型得到了方案间的群体优势关系；然后，提出了群体优势度指标、某个方案的群体评价一致性指标和备选方案集的群体评价平均一致性指标，用于确定备选方案集的全序关系。最后，通过算例分析，验证了本文所提出方法的可行性和合理性，有效解决了信息不完全工况下难以实现方案优选的问题。