基于反潜探测能力的舰队搜潜队形优化研究
2018-10-25张诗闵绍荣朱忍胜余明晖高艺哲
张诗,闵绍荣,朱忍胜,余明晖,高艺哲
1华中科技大学自动化学院,湖北武汉430074
2中国舰船研究设计中心,湖北武汉430064
0 引 言
在未来海战中,反潜战将是主要形式之一,贯穿于战争的全过程。水面舰艇编队的反潜效果显著。舰艇平台的探潜装备通过计算机网络联合,实现信息共享,构成一个互联、互通、互操作的综合探潜体系[1-3]。舰艇编队中各水面舰艇到目标的距离和舰艇间的相对位置关系是影响探测概率的重要因素[4-5],合适的反潜舰艇编队队形分布可提高编队的整体反潜能力。
国内外有关水面舰艇编队搜潜能力的研究,大多关注的是装备性能和搜索战术,针对队形优化的研究较少。一些文献中是提到过典型反潜队形的应用,但未给出科学的证明,只进行了简单的定性分析[6]。李浩等[6]分析了典型反潜队形(如菱形、人字形、梯形等),建立了编队反潜队形综合评判指标体系,并应用三角模糊综合评价法建立了编队反潜队形优选模型来优化队形。这类评估方法未考虑成员舰艇的具体位置分布,而反潜战中成员舰艇的具体位置是影响编队整体对潜搜索概率的关键。朱燕麒等[7]建立了基于反导探测能力的舰队队形优化模型,该模型需假设目标分布,适用于敌方分布较为固定的反导场景,对反潜场景不适用且未考虑队形编成的约束。
为此,本文拟讨论队形约束下舰艇分布间距对编队反潜探测能力的影响,基于覆盖面积最大化原则,优化舰艇编队反潜队形并给出舰艇坐标。拟研究的水面舰艇编队队形有横队、方位队、人字队和楔形队,设计了基于概率—距离函数的积分寻优法求解最大覆盖面积,进而得到最优分布间距。
1 问题描述
根据国外通常采用的编队组成形式,本文研究的水面舰艇搜潜编队由n艘舰艇组成,队形约束为横队、方位队、人字队或楔形队。搜潜编队航行到潜艇可能出现的区域后,以直线路径或锯齿形路径进行搜索;发现潜艇后,将速度调整为潜艇速度以跟踪潜艇。在搜索阶段,需对编队的队形排布进行优化设计,给出队形约束下各舰的位置坐标,以使反潜声呐对潜探测的协同效果发挥到最大。队形编成后,在整个搜潜过程中保持不变,实现在作战海域对敌方潜艇的最佳探测。
2 基于反潜探测能力的队形优化模型
2.1 模型假设与说明
基于反潜探测能力的队形优化模型基于如下假设:
1)舰艇间距相等,且统一调整间距。
2)在深度方向潜艇一般在声呐作用距离内,简化为研究在水平方向对潜艇的探测能力。
3)编队各舰协同作战[8],当编队中一艘舰艇发现目标,即认为舰艇编队实现了对目标的成功探测。
4)编队对目标点的探测概率大于等于阈值Pf时,认为成功发现了该目标。
2.2 基于反潜探测能力的队形优化模型构建
2.2.1 编队反潜探测能力分析
各舰的搜潜探测概率—距离函数为P(r)。根据舰壳声呐的一般性探测性能特点,其探测概率通常服从指数分布[9]:
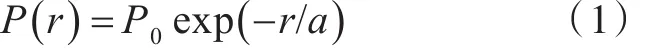
式中:a为声呐作用距离;r为探测距离;P0为探测概率的修正系数。
各舰艇声呐探测到的信息是共享的,因此,潜艇的探测概率受编队所有声呐的综合影响。信息共享的效果取决于数据融合方式、网络可靠性和数据传输速率等多种因素[10]。在理想情况下,海域内某一目标点被发现的联合概率为
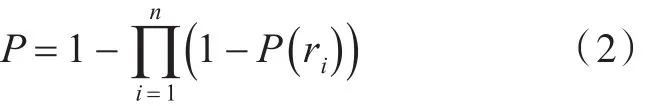
以3艘舰艇人字队形为例,分析队形对探测概率的影响。如图1所示,其他各舰位于基准舰两舷相同队列角上[11],其中d为分布间距,φ为队列角。对于某一探测目标点,若分布间距d改变,则舰艇1和舰艇3到该点的距离r1和r3随之改变,由式(2)可得,编队对该点的联合探测概率P也随之改变。当队形约束为单横队、方位队和楔形队时,上述分析也适用,故舰艇分布间距会影响编队探测概率。
2.2.2 覆盖范围定义
为了描述编队的对潜探测能力,本文特定义了覆盖范围这一指标,其面积记为S。若编队对某范围内所有位置的探测概率都大于等于探测概率阈值Pf,则称该范围为Pf的覆盖范围,Pf=(0,1]。由覆盖范围定义可知,该指标是以舰艇为中心,向外扩展计算周围各点的联合探测概率。被探测点的集合表征了编队的探测能力。
图2展示了由3艘舰艇组成的单横队在不同分布间距下的覆盖范围,由内到外分别表示编队探测概率为0.95,0.9,0.85,0.8的覆盖范围。由图可见,随着舰艇分布间距的增加,探测概率为0.95的覆盖范围慢慢分离。覆盖面积S随着间距的增加是先增大后减小,即声呐的协同作用先增强后减弱。
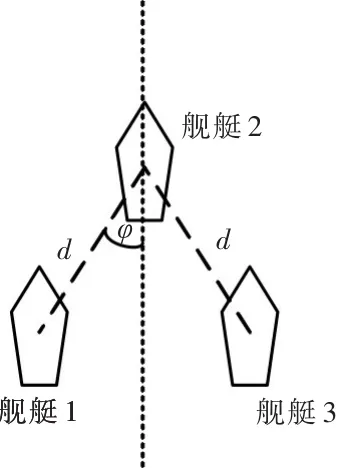
图1 人字队形示意图Fig.1 Herringbone formation diagram
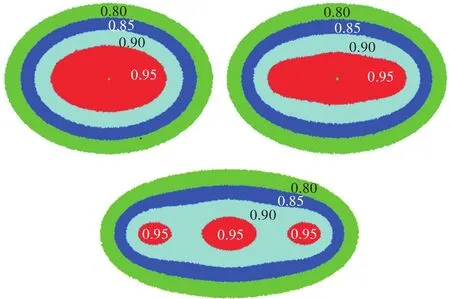
图2 覆盖面积随舰艇间距变化示意图Fig.2 Schematic diagram of coverage variation with ship spacing
2.3 基于反潜探测能力的队形优化模型
由于敌方潜艇位置和运动模式不确定,不能针对潜艇给出概率优化函数,故本文给出概率阈值,在舰船资源有限的情况下,保证舰队的探测范围尽量大,适用于搜潜场景。基于覆盖范围的定义,探测概率阈值Pf的覆盖范围越大,则编队在搜索过程中发现潜艇的可能性越大,编队探测能力越强。不同的舰艇分布间距对应不同的覆盖范围。因此,基于反潜探测能力的队形优化模型优化目标为
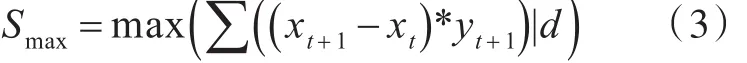
3 模型求解
若各艘舰艇的声呐互不通信,则可由探测概率—距离函数P(r)得到探测距离。以式(1)为例,探测概率Pf对应的最远探测距离为

当各舰的探测范围互不覆盖时,探测概率Pf的覆盖面积取值最大,为

实际作战中,编队具有完备的通信链路,各艘舰艇的声呐信息是共享的。编队对目标的探测概率由各艘舰艇与目标的相对位置联合确定,难以直接求解最大覆盖面积。为此,本文设计了基于概率—距离函数的积分寻优法,利用Matlab软件进行求解,求解流程如图3所示。针对不同舰艇分布间距,利用积分法求出覆盖面积后,绘制覆盖面积—间距关系曲线,寻找最优队形。基于概率—距离函数的积分寻优法支持不同舰艇探测性能的差异性,对舰艇进行排列组合,求出各个组合的最大覆盖范围,然后取最优最大覆盖范围,进而得到不同探测能力情况下的最优队形。
基于概率—距离函数的积分寻优法包括3个步骤。
步骤1:根据队形给出各舰坐标关于间距d的方程。
步骤2:求解分布间距d对应的覆盖面积S。
步骤2.1:当P=Pf时,求解横坐标x对应的纵坐标y;
其中,ρ为介质密度,ut为水平位移速度,wt为垂直位移速度, τxx,τzz为正应力,τxz为剪应力,λ,μ为介质的拉梅系数;c11=c33=λ+2μ,c13=λ,c44=μ。
步骤2.1.1:计算(x,y)到各舰艇的距离ri,由探测概率—距离函数P()r和式(2)得到该点的探测概率。
步骤2.1.2:判断该点的探测概率P与Pf的关系,若P≥Pf,令纵坐标y=y+Δ,跳转到步骤2.1.1;否则,结束循环,记录下当前的纵坐标y。
步骤2.2:判断横坐标x与(n+1)a/2的关系,若x<(n+1)a/2,令横坐标x=x+Δ ,跳转到步骤2.1;否则,结束循环,得到分布间距d对应的覆盖面积S=Δ∑y。
步骤3:判断分布间距d与2a的关系,若d<2a,令间距d=d+Δ,跳转到步骤2;否则,结束计算,绘制间距d和覆盖面积S的关系曲线,并得到Smax及其对应的间距dbest,从而得到各舰的位置坐标。

图3 求解流程图Fig.3 Solution flow chart
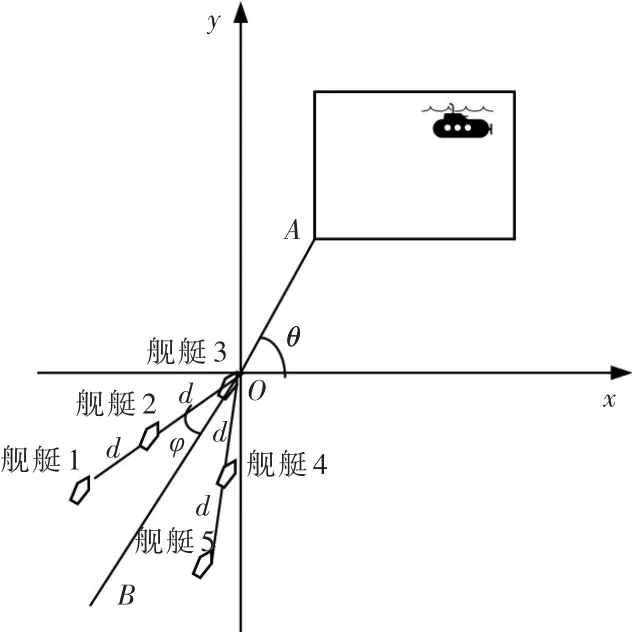
图4 坐标系示意图Fig.4 Schematic diagram of coordinate system
增量Δ取值越小,算法精度越高,可取Δ=0.01。
考虑到作战环境,在实际应用中,以平行于纬度为横轴,平行于经度为纵轴,以编队初始中心位置为坐标原点建立坐标系,如图4所示。利用上述方法可以得到各舰在海域上的经、纬度坐标,实现编队对潜最优探测能力。
以人字队形为例来表示舰艇坐标方程:
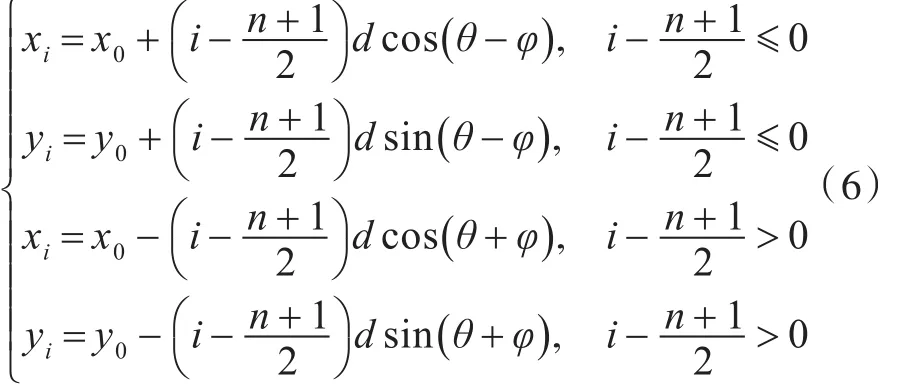
4 仿真分析
水面舰艇编队在执行搜潜任务时已知敌方潜艇初始发现海域,反潜编队布好人字队形,前往该区域。敌方潜艇的具体位置和运动模式未知,且运动范围可能超出该区域,故编队在前往途中以及整个搜索阶段都保持最大覆盖面积对应队形不变,以保证对潜最佳探测能力。参数如表1所示。

表1 仿真参数Table 1 Simulation parameters
4.1 不同队列角下覆盖范围的变化
令队形约束为人字队形,探测概率阈值Pf=0.8,舰艇数量n=5,研究两侧舰艇夹角φ=30°,45°,60°时,覆盖面积S随间距r的变化。仿真结果如图5所示。
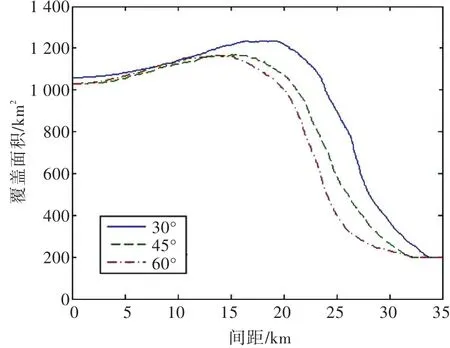
图5 覆盖面积随间距的变化(不同队列角)Fig.5 Variation of coverage area with ship spacing(different queue angles)
队形约束为人字形、两侧舰艇夹角φ=45°时,利用基于概率—距离函数的积分寻优法得到优化后的各舰坐标(表2)。

表2 人字队形各舰坐标Table 2 Ship coordinate of herringbone formation
由图5和表2所示的仿真结果可以得出:基于反潜探测能力的队形优化模型适用于不同的队列角。对潜探测覆盖范围随着舰艇分布间距的改变变化明显。随着舰艇间距的增加,覆盖面积先缓慢上升,在到达峰值后显著下降,最后趋于水平,表示声呐的协同作用减弱为0。由变化趋势可以看出,选择最大覆盖面积对应的编队分布能有效提升搜潜效率。
4.2 各种队形下覆盖范围的变化
令探测概率阈值Pf=0.8,舰艇数量n=5,研究单横队形、方位队形、人字队形和楔形队形的覆盖面积S随间距r增加的变化情况,并给出各舰坐标。仿真结果如图6所示。

图6 覆盖面积随间距的变化(不同队形)Fig.6 Variation of coverage area with ship spacing(different fleet formations)
由图6所示的仿真结果可以得出:基于反潜探测能力的队形优化模型适用于各种队形约束。对潜探测覆盖范围随舰艇分布间距的变化趋势与4.1节一致。人字队形和楔形队形在最优分布间距下的覆盖范围较大,单横队形和方位队在最优分布间距下的覆盖范围较小。
4.3 最优间距随探测概率阈值的变化
令队形约束为人字队形,舰艇数量n=5,研究最优间距rbest随探测概率阈值Pf的变化。仿真结果如图7所示。
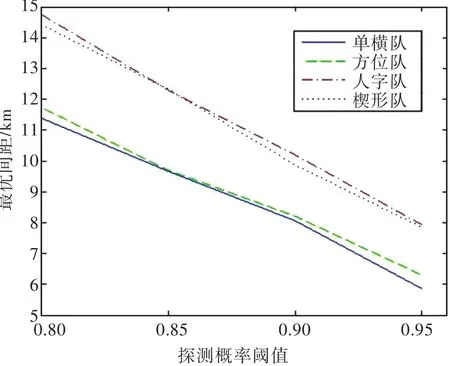
图7 最优间距与探测概率阈值的关系Fig.7 The relationship between optimal spacing and detectionprobability threshold
由图7所示的仿真结果可以得出:随着探测概率阈值的增加,最优间距减小。当搜索精度要求较高时,适当靠拢搜索阵型,搜索效果更佳。
4.4 覆盖面积随舰艇数量的变化
令探测概率阈值Pf=0.8,研究单横队形、方位队形、人字队形和楔形队形的最大覆盖面积Smax随舰艇数量n的变化。仿真结果如图8所示。
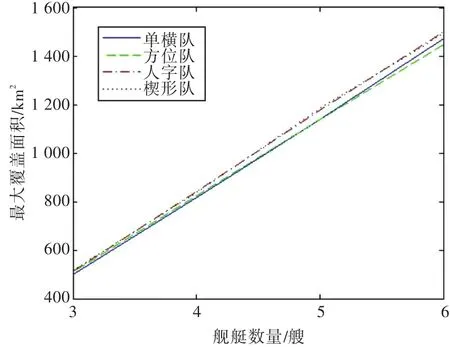
图8 最大覆盖面积与舰艇数量的关系Fig.8 The relationship between the maximum coverage area and the number of ships
由图8所示的仿真结果可以得出:覆盖面积与舰艇数目正相关,两者之间近似线性关系。在条件允许的情况下,适当提高舰艇数量,能达到更好的搜索效果。
5 结 语
基于反潜探测能力的水面舰艇编队搜潜队形优化模型和基于概率—距离函数的积分寻优法能够准确、快速地给出优化的队形方案和水面舰艇编队中各舰在海域上的坐标位置。模型不依赖潜艇位置和运动模型,具有一定的实用性,为合理运用和部署水面舰艇对潜搜索兵力提供了决策依据。
本文的队形优化主要基于反潜探测性能,在后续的研究中,应全面考虑队形编成所涉及的其他优化目标,提高其普适性。
