基于NESO的潜艇航向滑模控制器设计

陆斌杰，李文魁，陈尔明

1海军工程大学电气工程学院，湖北武汉 430033

2上海海军航保修理厂，上海200083

0 引言

潜艇在水面航行时，海浪干扰将严重影响其操舵控制。例如，由一阶海浪引起的振荡会造成自动舵的频繁操舵，从而导致控制品质恶化。基于此，海浪滤波器应运而生，用以帮助潜艇克服海浪的高频干扰，从而优化控制品质，并保持低噪运行状态。

在该研究领域，国内外相关学者已提出了诸如Kalman滤波器、一阶低通滤波器、无源滤波器等海浪滤波器［1-2］。Boutayeb等［3］提出，利用卡尔曼滤波方法计算观测增益时，系统需提供较准确的模型参数和噪声协方差矩阵，且难以对系统非线性部分开展鲁棒性分析工作。Esfahani等［4］发现，不依赖于精确数学模型的非线性扩张状态观测器（Nonlinear Extended State Observer，NESO）可以有效观测系统内扰和外扰，并且可对干扰估计值进行补偿。Cui等［5］提出，通过对NESO参数进行整定，即可使其具备滤波功能。Esfahani等［4］还发现，滑模控制（Sliding Mode Control，SMC）对系统参数摄动和外部干扰具有不敏感性，且易于工程实现。因此，本文拟提出一种基于NESO海浪滤波器的潜艇航向滑模控制策略，并设计基于双曲正切函数的双幂次趋近律以降低抖振。

1 扩张状态抗干扰观测器设计

引入干扰补偿控制并结合滑模控制的扩张状态抗干扰观测器控制结构如图1所示，图中：yd为系统期望输出；y为系统实际输出；uδ为滑模控制器输出；uD为经抗干扰观测器估计的干扰补偿控制输出；D为系统所受干扰；̂为扩张状态抗干扰观测器输出的干扰估计；uc为总控制输出。

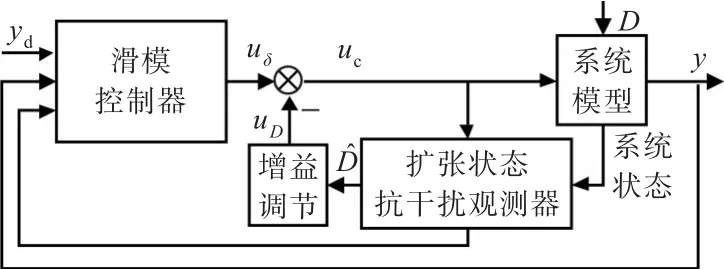
图1 系统控制结构Fig.1 System control structure

取系统模型的状态方程为

式中：x为系统状态变量；f为系统动态函数；n为控制量系数。

干扰估计值̂经增益调节后产生干扰补偿控制输出uD，将其输入控制环路可以减弱干扰影响。干扰估计误差为

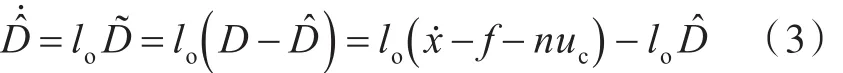
式中，lo为扩张状态抗干扰观测器的增益。

根据潜艇水平面运动模型，取三阶非线性扩张观测器，得

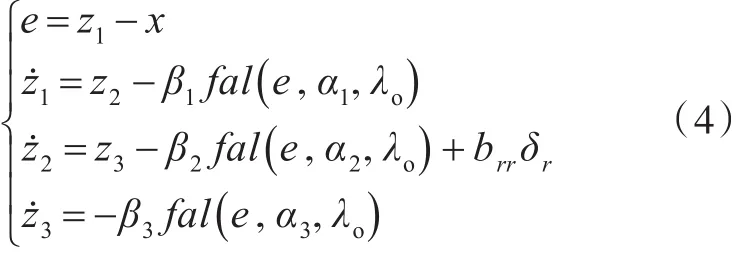
式中：e为观测误差；zi（i=1，2，3）为状态变量x的估计量；βi（i=1，2，3）为观测误差的反馈增益，其数值越大，跟踪越快，但滤波效果也越差；为非线性函数；brr为控制系数；δr为方向舵舵角。

其中

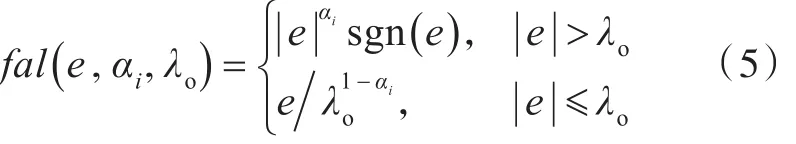
式中：0＜αi＜1（i=1，2，3），其值决定了跟踪速度；λo＞0，为线性区间宽度。

将̂转换为相应的补偿控制量uD，取。由图1可知，u=u-u，代入系统状态cδD方程（1），得

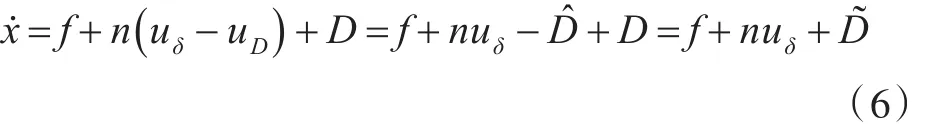
由式（6）可知，系统所受的总干扰由D降低为͂，即系统稳定性得以提高。

2 潜艇航向控制设计

2.1 潜艇水平面设计模型

本文中潜艇水平面设计模型的坐标系、名词术语、符号规则均采用ITTC和SNAME术语公报的体系［6］。固定坐标系（定系）E-ξηζ和运动坐标系（动系）o-xyz如图2所示。

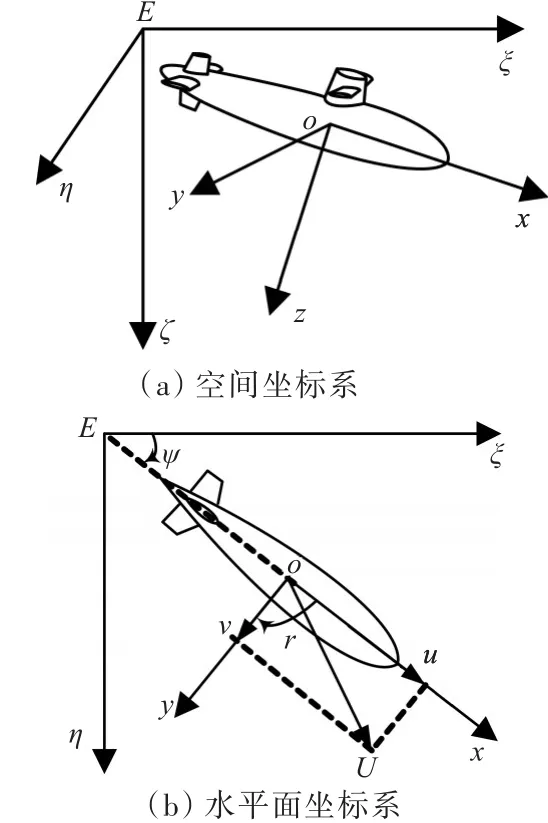
图2 固定坐标系和运动坐标系Fig.2 Fixed coordinate system and motion coordinate system

图中：ψ为航向；r为偏航角速度；v为横向速度；u为纵向速度；U为合成速度。本文采用潜艇水平面线性模型作为控制器设计模型［7］，即

其中，

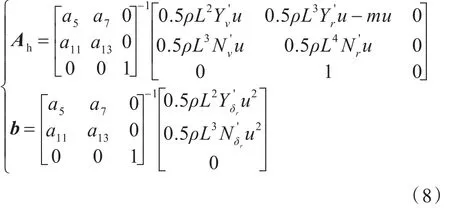
式中：ρ为海水密度；L为艇长；为速度水动力系数；m为质量；为舵角水动 力 系 数 ；，其 中为加速度水动力系数。

令x7=ψ，x8=ψ̇，则

2.2 海浪干扰模型

由于潜艇处于水面航行状态时其与水面舰船所受波浪力的影响大致相同，故可以采用PM波谱来表达其谱密度，即

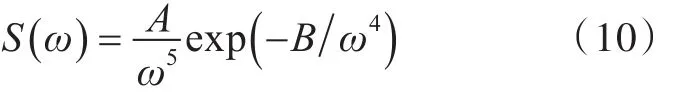
式中：A=0.008 1g2，其中g为重力加速度；ω为波浪圆频率；，其中H13为有义波高。

可将一阶浪频航向等效为由白噪声驱动的二阶惯性滤波器的响应［7］。设ξH为波幅，ψH为浪频航向，状态，则状态方程形式的线性浪频航向模型为

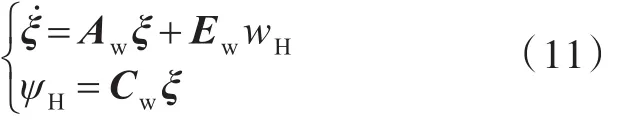
其中，

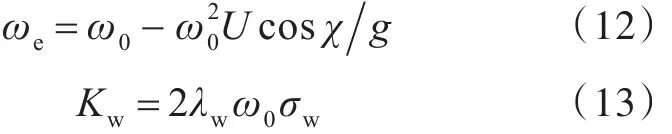
式（12）和式（13）中：ω0为海浪主导角频率；χ为海浪遭遇角；

线性海浪谱拟合如图3所示。

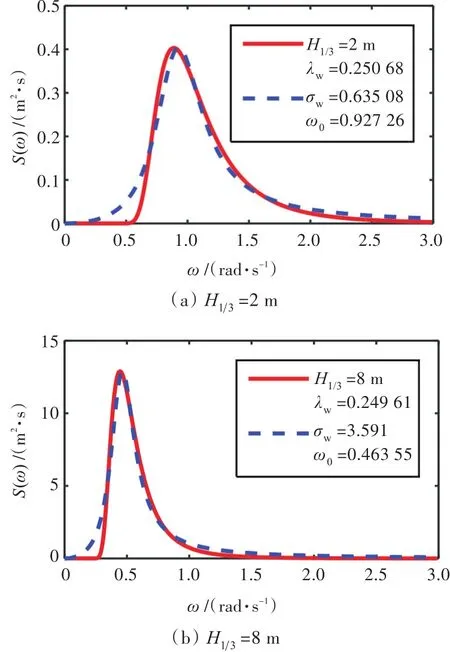
图3 线性海浪谱拟合Fig.3 Linear wave spectrum fitting

二阶低频慢漂力为［8］

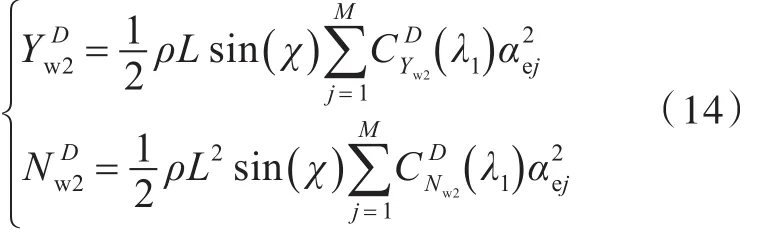
其中，

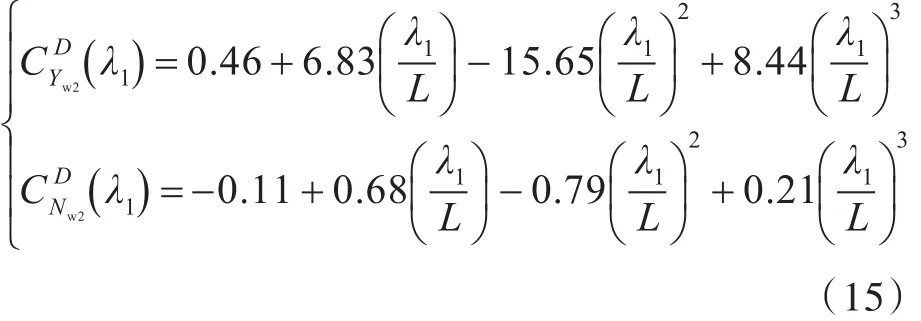
2.3 潜艇航向控制器设计

2.3.1 滑模控制律设计

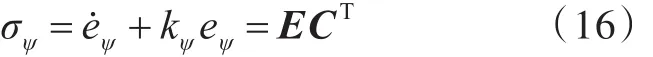
式中：kψ＞0，为可调参数；。

选取基于双曲正切函数的双幂次趋近律，则方向舵舵角δr的滑模控制律为

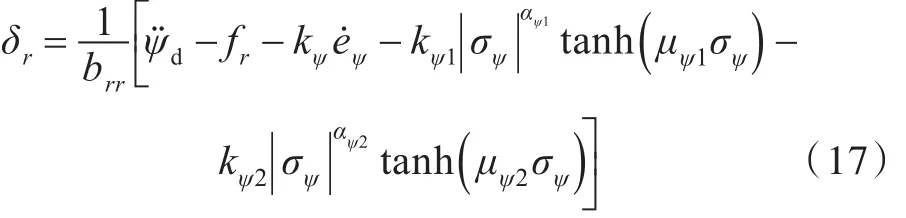
式 中 ：kψ1＞0 ，kψ2＞0 ，αψ1＞1 ，0＜αψ2＜1 ，μψ1＞0，μψ2＞0，均为可调参数。

采用连续光滑的双曲正切函数以降低抖振，其表达式为

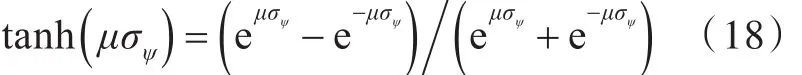
式中：μ＞0，为待定调节系数，其值决定了双曲正切函数拐点的变化速率。

选取Lyapunov函数Vψ，即

对式（19）求导，得

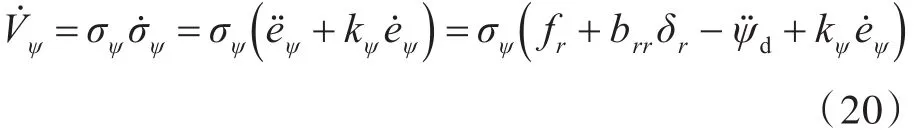
将式（17）代入式（20），得

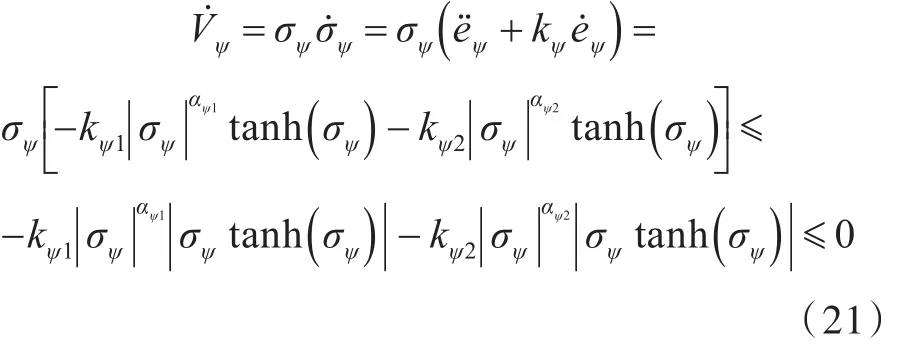
2.3.2 扩张状态抗干扰观测器设计

式（3）即为航向抗干扰观测器方程，则航向抗干扰观测误差方程为式中，为干扰估计量。

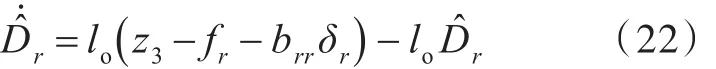
方向舵补偿控制律uDr为

结合式（17）和式（23），方向舵的总控制律δrc的表达式为

3 仿真分析

仿真对象为潜艇水平面线性操纵运动模型，其水动力系数可以参考文献［9］，部分水动力系数如表1所示。

表1 潜艇的部分水动力系数Table1 The partial hydrodynamic coefficients of the submarine

舵机系统可视为由积分环节和负反馈组成的一阶惯性环节，其动态模型为

式中：δ0为舵机输出的实际舵角；δc为指令舵角；，为舵机时间常数，其中δpb为回路比例带，一般为 5°，=2～3.5(°)s，为最大舵速，最大舵角δmax=30°。舵角与舵速都具有饱和特性，即且。

当航速为10 kn时，系统参数为

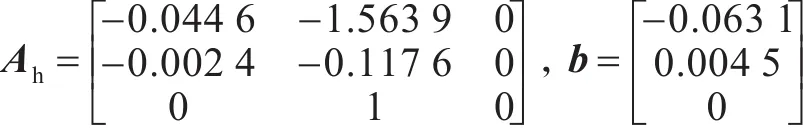
当航速为15 kn时，系统参数为

对于不同的海况等级，NESO滤波器的参数选取也有所不同。低海况时，偏重跟踪速度，可以适当增大βi并适当减小λo以取得更好的跟踪效果；反之，高海况时，偏重滤波效果，可以适当减小βi并适当增大λo以取得更好的滤波效果。本文仿真分析中，NESO滤波器参数如表2所示。

在不同的航速、海况和浪向下，有/无NESO滤波的航向滑模控制效果对比结果如图4～图9所示。

由图4和图5可知，0级海况时，在不同航速下基于NESO滤波的SMC均能快速无超调地跟踪指令航向，且打舵平滑无抖振。

由图6和图7可知，当U=10 kn，4级海况时，无NESO滤波的SMC能够对航向实现较好的控制，但稳定航行时舵角会出现高频的小幅抖动；加入NESO滤波后，航向控制效果无明显差异，但稳定航向时打舵的舵频和舵幅均明显降低，即打舵更为平滑。

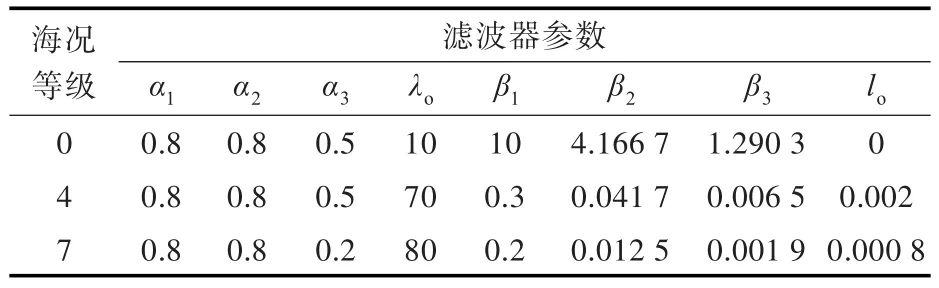
表2 NESO滤波器参数Table2 The parameters of NESO filter

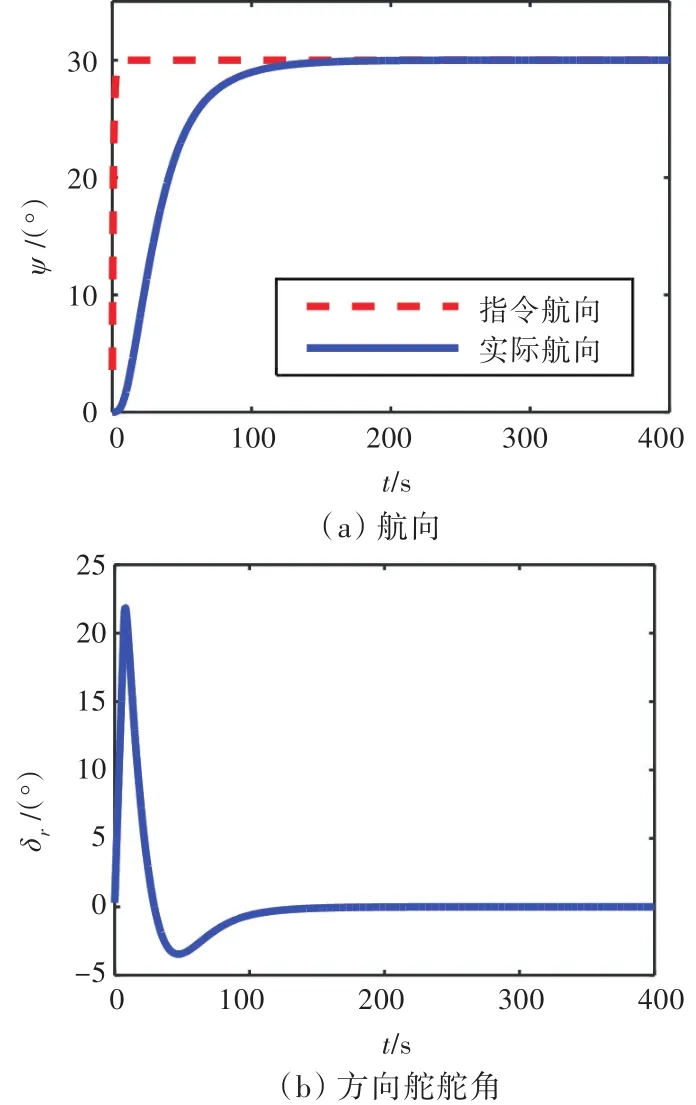
图4 基于NESO的滑模航向控制（U=10 kn，0级海况）Fig.4 SMC heading control based on NESO（U=10 kn，Sea state 0）

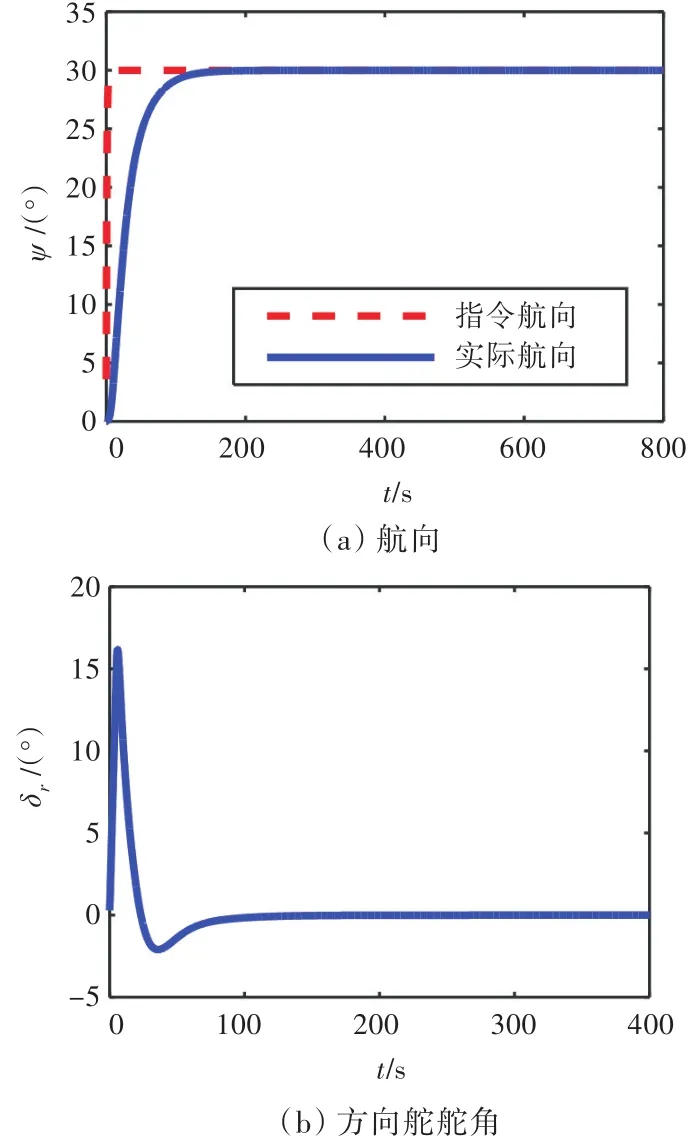
图5 基于NESO的滑模航向控制（U=15 kn，0级海况）Fig.5 SMC heading control based on NESO（U=15 kn，Sea state 0）

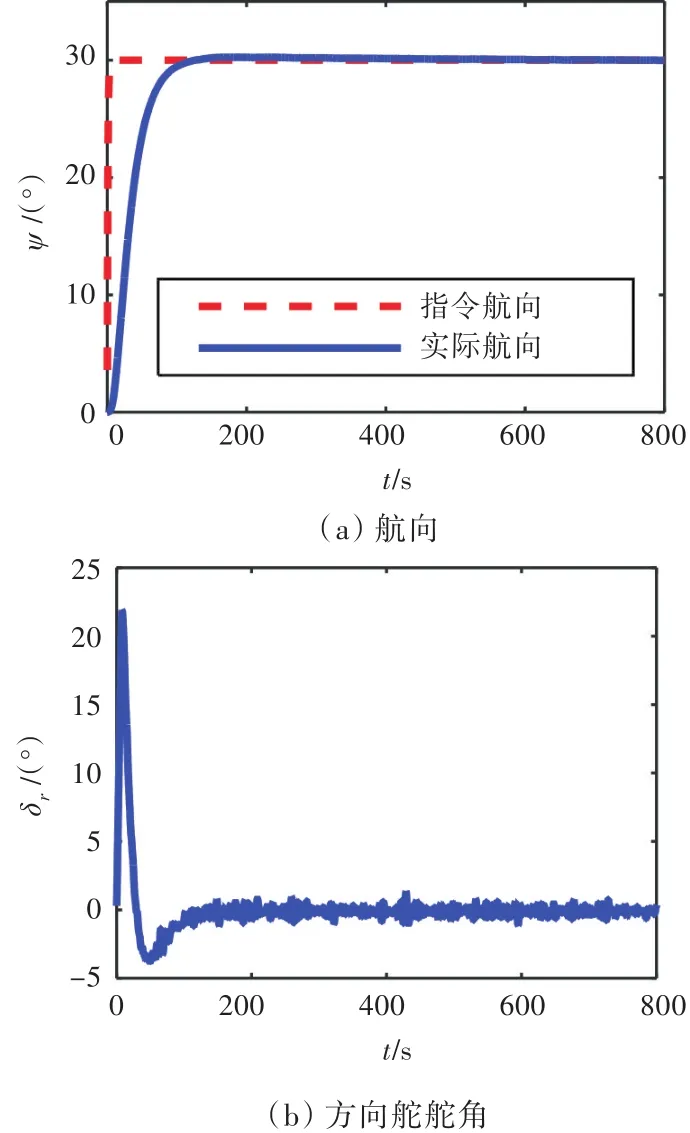
图6 无NESO的滑模航向控制（U=10 kn，4级海况，χ=60°）Fig.6 SMC heading control without NESO（U=10 kn，Sea state 4，χ=60°）

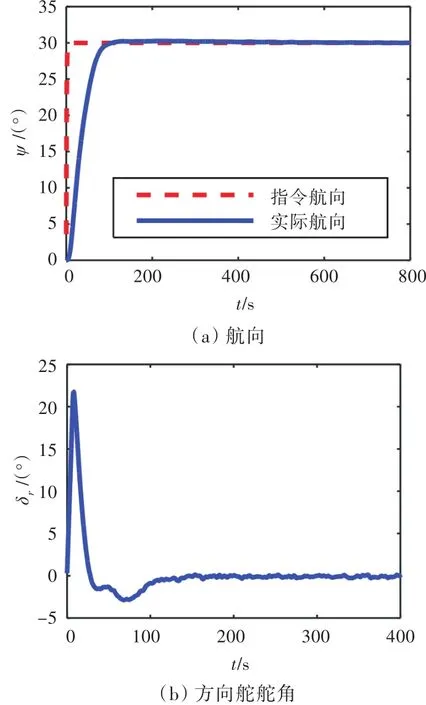
图7 基于NESO的滑模航向控制（U=15 kn，4级海况，χ=60°）Fig.7 SMC heading control based on NESO（U=15 kn，Sea state 4，χ=60°）

由图8和图9可知，当U=15 kn，7级海况时，无滤波的SMC能够对航向实现快速控制，但稳定航行时，由于二阶波浪力的作用，出现了约0.6°的稳态误差且舵角出现高频抖动。加入NESO滤波后，当实际航向接近指令航向时，航向出现了小幅波动并产生了约0.9°的超调，这是由于NESO滤波器突出了滤波功能但降低了跟踪功能，导致航向和航向变化率的跟踪效果变差所致，可以通过调节滤波器参数来进行改善。稳定航行时，稳态误差逐渐趋于0°，可以实现高精度航向控制，且打舵的舵频和舵幅均明显降低，即打舵更为平滑。

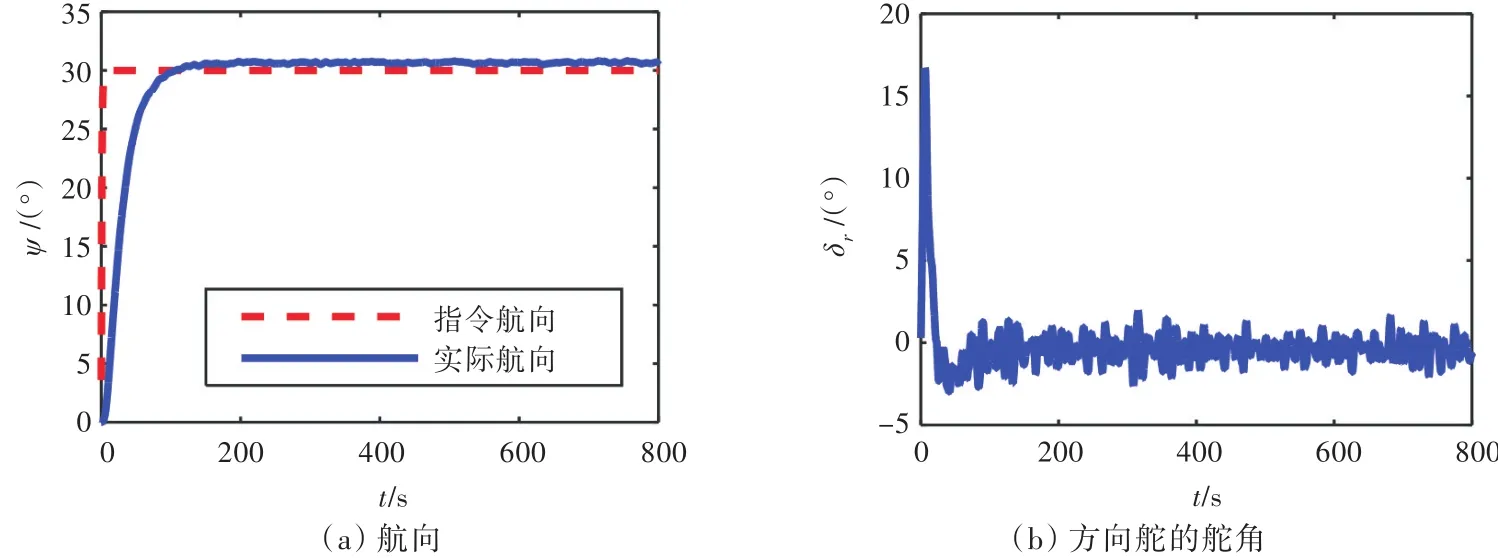
图8 无NESO的滑模航向控制（U=15 kn，7级海况，χ=120°）Fig.8 SMC heading control without NESO（U=15 kn，Sea state 7，χ=120°）

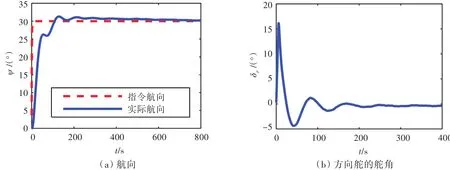
图9 基于NESO的滑模航向控制（U=15 kn，7级海况，χ=120°）Fig.9 SMC heading control based on NESO（U=15 kn，Sea state 7，χ=120°）

综上所述，基于NESO的SMC可以快速无超调地跟踪指令航向，且打舵平滑无抖振。

4 结 语

针对潜艇水面航行时的航向控制问题，提出了一种基于双曲正切函数的双幂次趋近律，可以有效降低滑模控制的抖振；同时设计了非线性状态观测器，利用NESO的滤波功能来滤除高频海浪，有效降低了打舵舵频和舵幅，从而实现了低噪和节能操舵的目的。通过调节滤波器参数，可以在不同航速、海况和浪向下实现低噪、快速、高精度的航向控制效果。后期拟针对潜艇非线性模型的控制仿真和NESO参数的整定问题开展进一步的研究，通过平衡滤波效果和跟踪速度来达到最优效果。