椭圆度影响下金属波纹管柱失稳外压计算模型的建立与分析

魏 晨 杨 阳

（1.四川建筑职业技术学院土木工程系，四川德阳618000；2.四川建筑职业技术学院电气工程系，四川德阳618000）

0 引言

外压作用下金属波纹管柱的失稳变形在工程上是个常见问题，是一种常见的结构破坏形式。美国石油天然气协会管道委员会于1984年分三阶段对管道的应力破坏现象进行了研究，完成了大量实验工作，在此基础上发布了API-5C3标准，为设备安全校核提供了依据。实验和工程中发现，API给出的计算公式与实际管道失稳外压有较大出入，这主要是由于API-5C3未考虑金属管的几何缺陷椭圆度。

1 有限元分析

由于要讨论椭圆度单因素对金属波纹管失稳外压的影响，故必须消除不同管道材料、不同管道壁厚带来的影响，因此分析从两方面展开：（1）不同材料不同椭圆度下金属管试样分析；（2）不同壁厚不同椭圆度下金属管试样分析。最后将两方面结果综合整理，得到椭圆度单因素对金属波纹管失稳外压的影响结论。

1.1 不同材料不同椭圆度

设计分析外压50 MPa，壁厚20 mm，金属波纹管试样变形情况如图1所示。

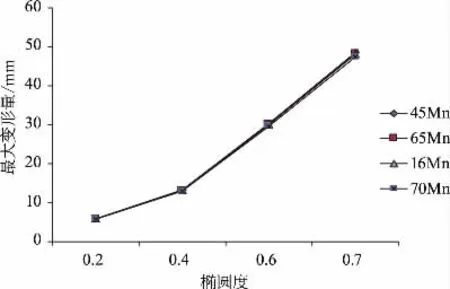
图1 不同椭圆度不同材质变形量

（1）弹性模量相差最大的材料是45Mn与70Mn，45Mn是70Mn的97.7%；对应最大变形量，在椭圆度分别取0.2、0.4、0.6、0.7时45Mn分别是70Mn的102.4%、102.4%、102.4%、102.4%。

（2）泊松比相差最大的材料是45Mn与16Mn，45Mn是16Mn的90.3%；对应最大变形量，在椭圆度分别取0.2、0.4、0.6、0.7时45Mn分别是16Mn的101.0%、101.0%、101.0%、101.0%。

（3）最低抗拉强度相差最大的材料是45Mn与70Mn，45Mn是70Mn的79%；在椭圆度分别取0.2、0.4、0.6、0.7时45Mn分别是70Mn的102.4%、102.4%、102.4%、102.4%。

（4）在椭圆度分别取0.2、0.4、0.6、0.7时，同种材料的最大变形量呈递增趋势且趋势明显，最小增幅均在60%。

总结上述结论得出，材料与椭圆度皆对金属波纹管失稳外压形成影响，但材料的影响不显著，椭圆度对金属波纹管可能的失稳情况影响权值更大，需明确椭圆度与金属波纹管失稳外压间的关系。

1.2 不同壁厚不同椭圆度

设计分析外压50 MPa，材料65Mn，金属波纹管试样变形情况如图2所示。

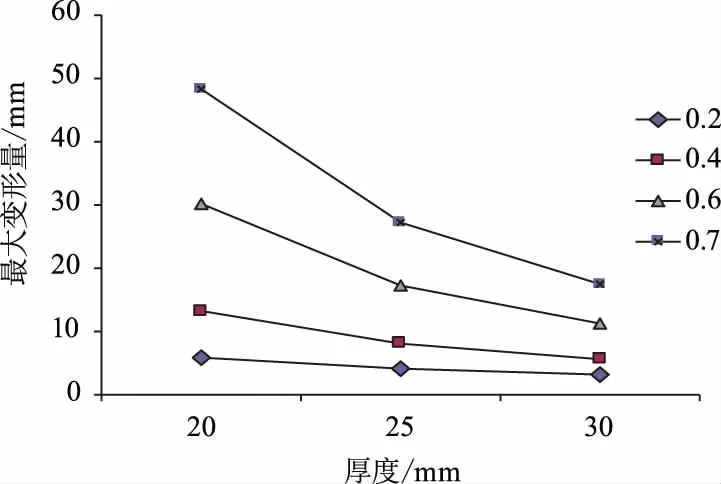
图2 不同壁厚下不同椭圆度的变形曲线图

（1）一定椭圆度下，随着壁厚的增加，最大变形量减小。在椭圆度分别为0.2、0.4、0.6、0.7时，随着管道壁厚由20 mm增加到30 mm，最大变形量减小幅度分别为29.8%、38.9%、42.8%、43.6%。在椭圆度较低时，壁厚对最大变形量的影响不明显，随着椭圆度的增加，壁厚的影响逐渐显著。

（2）一定壁厚下，随着椭圆度增加，最大变形量增大。在壁厚分别取20 mm、25 mm、30 mm时，随着椭圆度由0.2增加到0.7，不同椭圆度下变形量分别为初始的7.2倍、5.6倍、5.6倍。

1)由于不受信号灯控制，晋元庄路口东向北右转车辆对南向北直行车辆影响非常严重，尤其是该方向公交车辆线路较多，影响更为严重；同时，原有相位采用南北直行和北向东左转同时放行，虽然南向北直行施行早断，再放行左转，但在早晚高峰时对南向北直行的车辆影响也比较严重；

总结上述结论得出，在小椭圆度的情况下，材料对金属波纹管最大变形量的影响应予以考虑，应该将材料壁厚作为金属波纹管失稳的一个因素考虑分析，但与椭圆度单因素相比其影响程度依旧有限。

2 理论分析

2.1 海底管道多因素的失稳模型

金属波纹管失稳是压力、轴向力、弯曲以及管子不圆度等因素综合作用的结果，在只考虑外压的简单外界环境下，已有Bresse公式可以解决。在较复杂环境下讨论金属波纹管的失稳，有海底管道屈曲失稳模型可供参考，从这个模型出发，导出椭圆度单因素对金属波纹管失稳外压影响的计算模型。

挪威船级社（DNV）海洋管道系统规范规定，弯矩M与外压Pe的关系如下：

式中，Mcr为临界弯矩；Pcr为临界外压；α为弯矩系数。

2.2 含椭圆度缺陷金属波纹管失稳外压计算模型

椭圆度的定义如下：

式中，T为椭圆度；Dmax、Dmin分别为最大、最小金属管外径。

假设椭圆的长轴在X轴，短轴在Y轴，则椭圆的标准方程为：

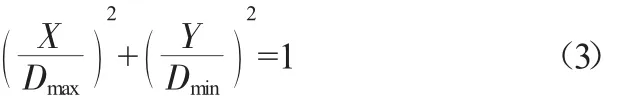
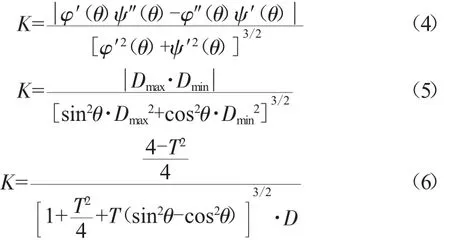
式（1）是理想管道在受到外压与弯矩联合作用下的失稳模型，把M=K·EI代入就得到在椭圆度单因素影响下金属波纹管失稳外压的计算模型，模型中EI对结果没影响，此处杨氏模量为材料的杨氏模量，非金属波纹管对应值，忽略了材料成型对材料物理性质的影响。此处只考虑了椭圆度与失稳外压的关系，金属波纹管失稳外压除与椭圆度这一因素有关外还与金属管径厚比、金属管壁厚均匀度有关，模型中把椭圆度与金属管弯矩联系起来，利用前人研究结果，间接找到椭圆度与失稳外压的关系。综上有必要对模型进行误差修正，对式（6）乘以修正系数10-3，得到最终计算模型：

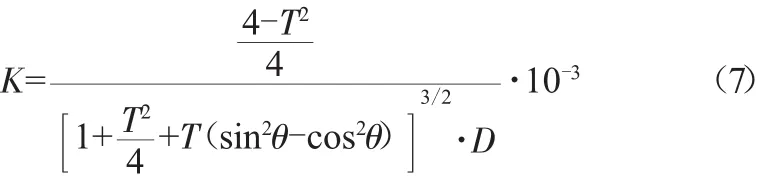
对金属波纹管失稳外压模型进行分析可得：

（1）含椭圆度金属波纹管，在椭圆度一定时，管子长轴两处弯矩最先达到最大，也就是金属波纹管的失稳最先发生在长轴两侧，在管子短轴两处弯矩最小，也就是管子短轴处发生失稳最困难。

（2）椭圆度项是递减的，即随着椭圆度的增大，外压项会偏大，从安全角度出发，改写模型为：

（3）导出含椭圆度金属波纹管失稳外压计算模型：

（4）极限弯矩可由弯曲应力公式得到，使用模型验证文献[1]中D/t=12.8时的失稳压力，结果如表1所示。

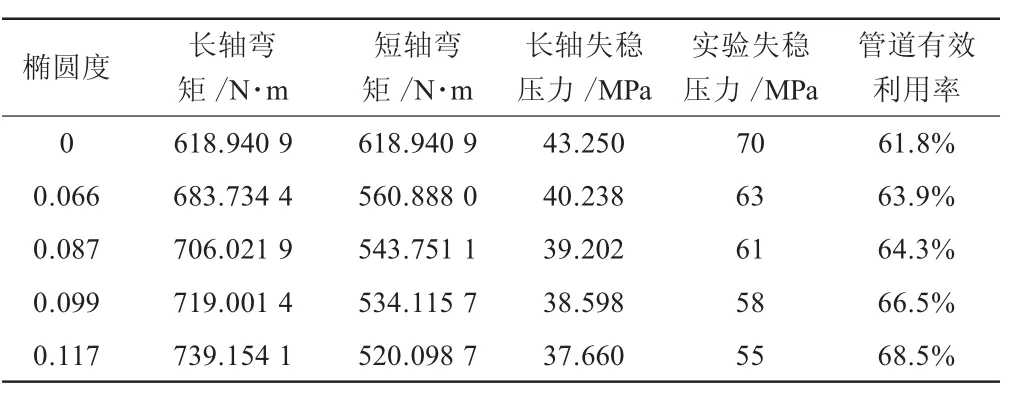
表1 模型计算失稳压力与实验失稳压力

3 结论

（1）金属波纹管横截面上的失稳压力是随角度分布的不同而异的，金属管的失稳在截面长轴处最先发生，故长轴处允许工作压力较截面其他部位的允许工作压力都要小，本文建立的含椭圆度金属波纹管失稳外压计算模型从安全角度出发用长轴处失稳压力代表整个金属管失稳压力，模型保留了相对大的安全裕度。金属管失稳不管发生在什么部位，已经存在了安全隐患，尽管用长轴处的失稳压力来代表整个金属波纹管的失稳压力比较保守，但依旧可以使用长轴处失稳压力代表整个管线失稳压力。

（2）虽然由模型推出的理论失稳压力较保守，但实际管线利用率依旧在60%～70%，本文建立的计算模型既能对金属波纹管的正常维护使用进行指导，又不会导致金属管的不必要更换而造成浪费，具有现实指导意义。