基于MATLAB倒立摆可视化建模仿真与控制

张新荣，马 杰，张才斗，吴学前

(1.长安大学 道路施工技术与装备教育部重点实验室，陕西 西安 710064；2.陕西工业职业技术学院 机械工程学院，陕西 咸阳 712000)

0 引 言

倒立摆作为教学、科研、产品开发过程中经常使用的研究和实验对象，一直被科研人员当作机械系统控制研究中的主要工具之一。作为典型的非线性、强耦合、多变量的不稳定系统，其可以直观的展现控制理论中许多经典抽象的概念，如系统的快速性、稳定性、抗干扰能力等[1-3]。目前多种控制算法均被应用于倒立摆的控制，如模糊控制、自适应控制、变结构控制及经典的PID控制等，显然倒立摆系统已成为验证各种控制理论的有力平台[4-8]。

文献[9]介绍了基于MATLAB的倒立摆控制算法及仿真，通过建立其数学模型，在MATLAB上进行3种控制方法的对比仿真分析；文献[10]分析了直线一级倒立摆的建模过程，采用MATLAB进行了仿真分析。在倒立摆建模、仿真和控制研究中使用最多的方法是理论建模，也可以采用Adams、Ansys、Pro/E、Solidworks等软件进行物理建模和仿真。文献[11]利用Pro/E与SimMechanics对曲柄摇杆机构进行联合仿真，并应用在机械原理教学中；文献[12]提出在Simulink和SimMechanics环境下进行动力学建模与分析的计算机辅助方法，对六自由度并联机器人动力学模型进行充分验证和分析；文献[13]提出了利用三维Pro/E模型转换成SimMechanics模型的建模方法，建立三自由度并联机器人机械系统模型，并设计PID控制器模型进行仿真分析；文献[14]基于Matlab/SimMechanics平台建立了3-RPS型并联机器人仿真模型，进行运动学仿真对比研究，验证了该建模方法的正确性。

本文提出使用Pro/E和Matlab/Simulink中的SimMechanics工具箱完成机械系统建模，利用Matlab强大的科学计算能力在Simulnk中完成控制算法仿真，在此基础上直接用于实物控制，实现了系统的建模、仿真和控制的集成，极大地提高了系统分析与产品开发效率。该方法使得复杂系统建模可视化、简化了理论推导、提高了建模的可靠性，可用于控制算法的仿真实验、控制器在环PIL(processor-in-the-loop)以及硬件在环HIL(hardware-in-the-loop)实验中。首先基于Pro/E软件建立环形一级倒立摆精确三维物理模型，联合SimMechanics将该模型导入Matlab/Simulink中，然后在Simulink中加入控制算法，进行联合仿真，并通过环形倒立摆控制实验验证仿真结果，最后给出结论。

1 环形倒立摆建模

SimMechanics工具箱本身可以对被控对象进行物理建模，但相比于三维建模软件其功能相对较弱，因此，本文采用Pro/E三维建模软件对环形倒立摆进行物理建模，代替常用的理论分析推导法建立数学模型，其流程如图1所示。三维模型绘制后，在Pro/E软件里安装SimMechanics Link接口插件，并以.XML文件导出该模型，然后在Matlab中导入这个.XML文件，于是在Matlab中即可自动生成环形倒立摆的SimMechanics仿真模型框架。模型生成后在Simulink中试运行，检查模型是否有误，各模块质量是否与测量结果一致。这种建模方式得到的控制模型，对数学基础要求低，少了繁琐的数学推导过程，从而减少不必要的可能的推导错误，可以更加准确地表达出实际的被控对象，使得建立的模型更加准确、可靠。

图1 建模流程

1.1 环形一级倒立摆Pro/E三维模型

为了准确建立控制对象的模型，首先对实验室的环形一级倒立摆系统进行了测绘，如图2水平连杆结构尺寸，对各零件形状尺寸进行精确测量记录。表1为主要零部件几何和物理参数。在此基础上，利用Pro/E三维建模软件建立各零件的准确模型。零件模型绘制过程中，各零件的密度、质量也要进行相应设置并保存。零件绘制完成后对各零件进行精确约束装配，实现与实验室倒立摆相同的运动效果，最终的环形一级倒立摆装配体如图3所示。

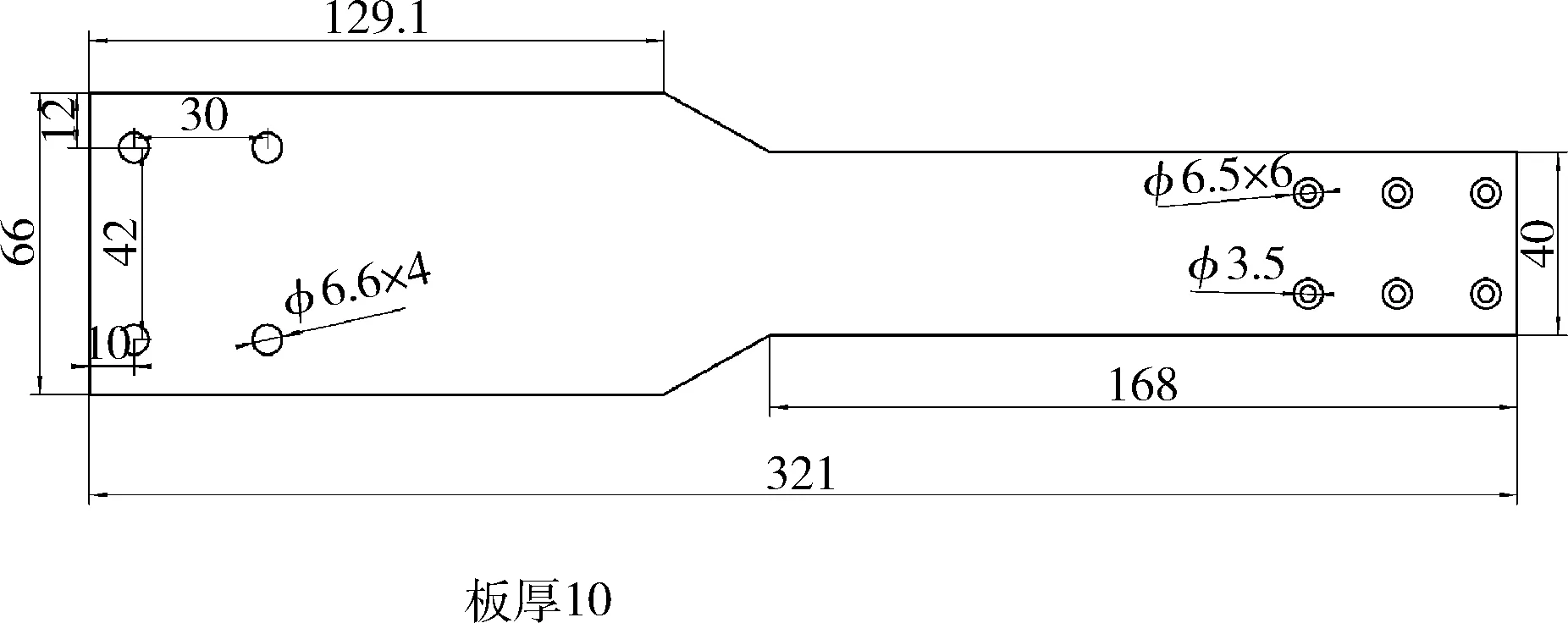
图2 水平连杆结构

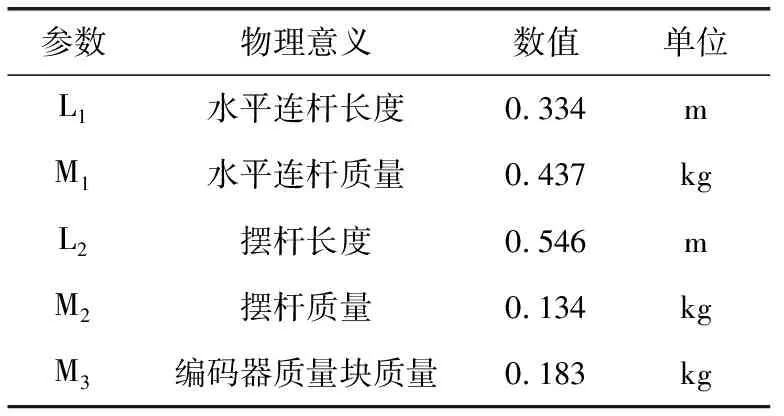
表1 环形倒立摆参数

1.2 环形一级倒立摆Matlab/SimMechanics仿真模型

不同于多数的拉格朗日数学计算建模，SimMecha-nics作为一种全新的物理建模方式，可以轻松的对及其复杂的机械系统进行快速的建模仿真。Simulink环境下的SimMechanics工具箱提供了快速的建模工具，可以将表示系统各部件及连接关系的模块通过Simulink窗口展现出来，并通过其自身提供的检测与驱动模块和普通的Simulink模块完成搭接，组成一个完整的仿真系统。充分利用Matlab的科学计算能力及Simulink动态仿真能力，获得整个系统的动态仿真结果，并可以将仿真三维动态图形展示出来。

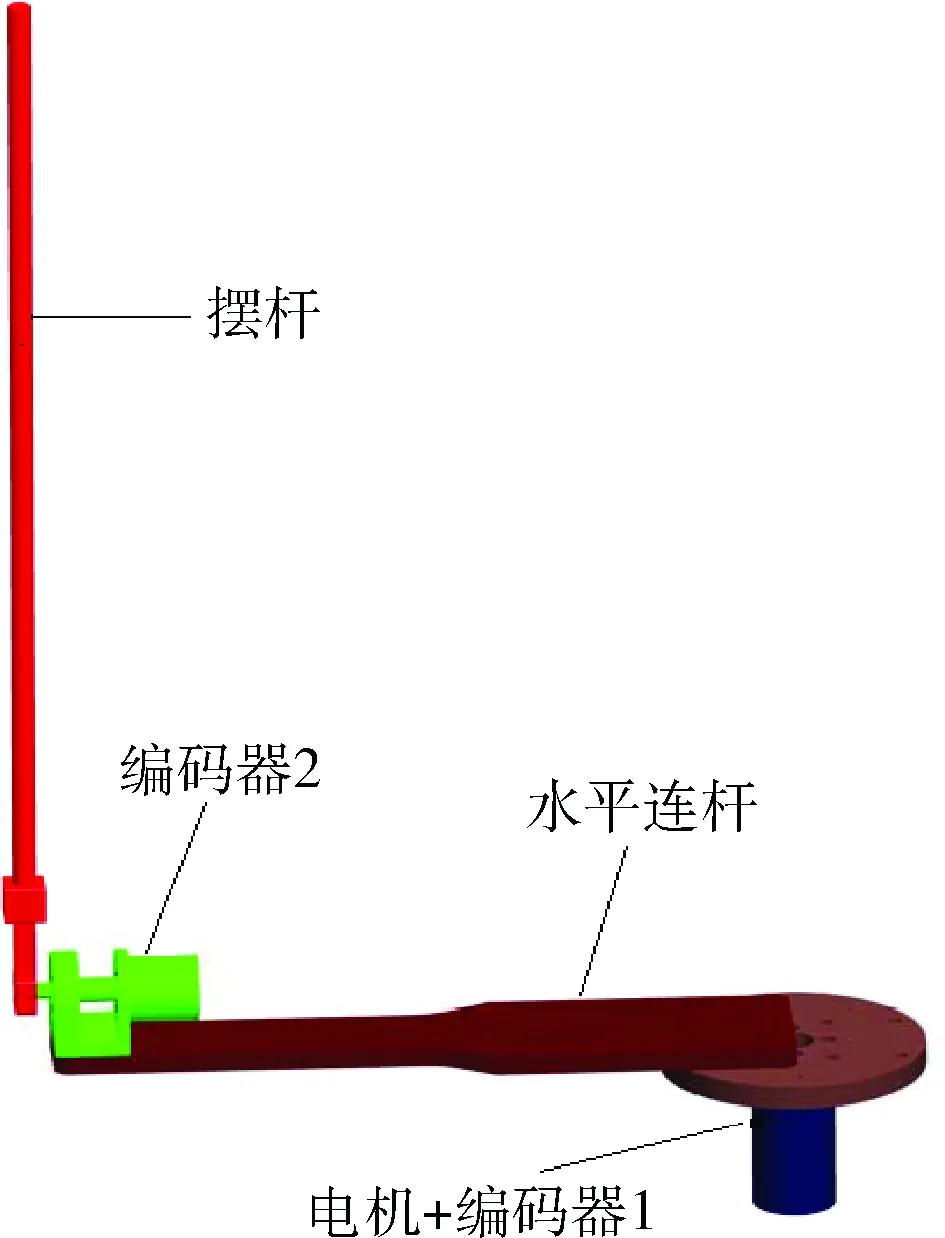
图3 环形一级倒立摆三维模型

在MATLAB中读取Pro/E导出的.XML文件，导入Simulink中生成环形一级倒立摆系统SimMechanics模型，图4所示为导入的初始模型。SimMechanics模型中所有模块的属性，如各模块质量、转动惯量、坐标位置等均根据三维模型自动导入。对于Pro/E装配基准、顺序的不同，此处导入的模块连接形式也会有所不同。图4中我们可以看到，生成的模型图主要包括的SimMechanics模块有：刚体模块组的机架和刚体、转动副模块组中的旋转模块。导入后各主要模块参数见表2。这些模块只是通过SimMechanics Link导入的环形倒立摆物理模型，相当于数学推导得到的倒立摆数学模型，要与普通的Simulink模块进行信息交换，还需要加入其它一些激励、控制和测试模块等，如控制器模块、检测与驱动模块、示波器模块等作为连接，进行控制系统仿真设计。

图4 环形一级倒立摆SimMechanics模型

表2 SimMechanics模块参数

2 控制器设计及仿真

导入到Matlab中的SimMechanics物理模型可以被认为是被控对象，在仿真时系统会将其自动转换为数学模型。仿真过程中水平连杆的角度θ1从Revolute旋转副连接的encoder1编码器输出，摆杆的角度θ2从encoder2编码器模块转轴中进行输出，而电机输出的控制力矩即设计的控制力矩则从圆盘的Revolute加入。为此，需要从SimMecha-nics库中加入与Simulink连接的驱动模块和角度检测模块，图4所示的模型已经加入了驱动模块和检测模块。

2.1 PID控制

PID控制作为一种经典的线性控制调节器，其控制方法已发展完善且在工业生产中得到极其广泛的应用。对被控对象的输出值与参考值的偏差，进行比例、积分、微分下的控制。

建立如图5中A所示的PID控制系统，Plant模块为前面建立的环形倒立摆模型(图2)经过封装后的模块，PID模块为Simulink库中自带模块。仿真过程中设置倒立摆摆杆与垂直向上方向的角度θ2在仿真初始时刻其起始角度为0.1 rad。通过Matlab/Simulink中对PID控制器的仿真调节工具，经过仿真最终选定PID控制参数为：KP=48，Ti=100，Td=7。点击运行后，系统会自动打开三维模型动态仿真图，与用Pro/E绘制的模型完全一致，更加立体、直观地显示出仿真过程，包括连杆转动情况、摆杆稳定情况等。

图5 仿真控制框架

2.2 极点配置法

极点配置法作为一种线性最优控制，对控制对象的状态空间模型进行分析，设计出合理的控制参数。极点配置法的控制规律为：u(t)=-Kx+v，其中u(t)为输入控制力矩，x为状态，K为状态反馈矩阵。

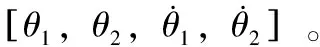
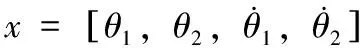
图6是在Simulink上仿真得到的环形一级倒立摆模型在PID及极点配置控制下的摆杆响应曲线。

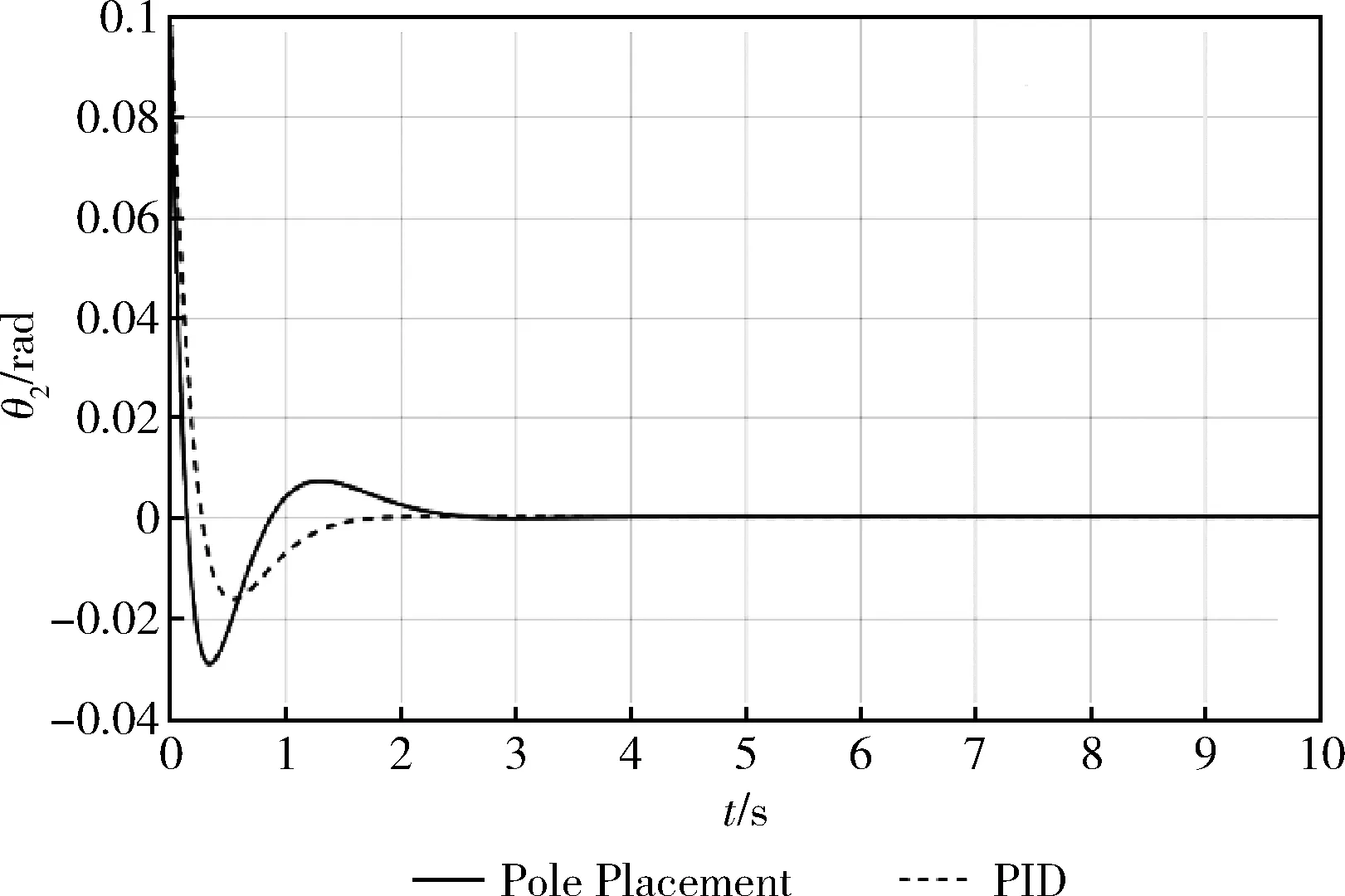
图6 仿真曲线结果

从摆杆响应曲线可以看出，在初始角度为θ2(0)=0.1rad的情况下，控制器可以快速响应，将倒立摆稳定在垂直倒立位置。且PID控制器比极点配置法响应的更快，超调更小。

3 实验及结果分析

本文提出的建模方法实际上相当于快速、准确地建立起了被控对象的物理和数学模型，为设计和验证控制算法提供了一个可靠的仿真平台。为了进一步验证此方法的有效性，可以针对实际系统进行实验验证。利用固高的环形倒立一级摆作为实验平台，其参数见表1。搭建如图7所示的实时控制系统，与前面的仿真系统相同，该系统工作在Windows7环境下，控制算法基于Matlab2012b开发，控制参数选择仿真时得到的数值。

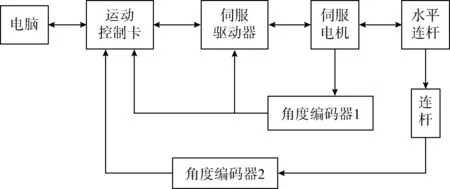
图7 倒立摆实时控制系统

利用Simulink设计的控制算法经过前面的仿真实验后得到了较好的控制效果，这里通过运动控制卡(GT400)将控制指令发出，驱动伺服电机(MSMJ022G1U)的转动。伺服电机驱动水平连杆从而控制摆杆在指定位置；水平连杆角度θ1通过电机转台相连接的编码器1(OVW2-06-2MD)反馈回伺服驱动器及运动控制卡，摆杆的角度θ2通过与其相连的编码器2送回运动控制卡，运动控制卡再将这些信息反馈给控制程序，实现闭环实时控制。图8所示为实验控制设备及环形倒立摆。

图8 环形倒立摆实时控制实验

通过Simulink平台可以很方便地将运动控制卡送来的信息保存起来，方便进一步分析。图9为PID控制算法及极点配置法用于实时控制的实验结果曲线。和仿真实验一样，也为方便对比，实时控制实验过程中摆杆的起始角度θ2(0)=0.1 rad。由于仿真时采用的各种信号都为理想信号，实验结果曲线与仿真曲线存在一定差异，但从总体趋势中可以看到实验与仿真结果基本一致。从两组曲线中我们可以看到PID控制下的摆杆响应更快、更稳定。验证了我们利用Pro/E与SimMechanics联合建模的这种方法对于环形倒立摆控制研究具有方便、可靠、直观、高效的特点。

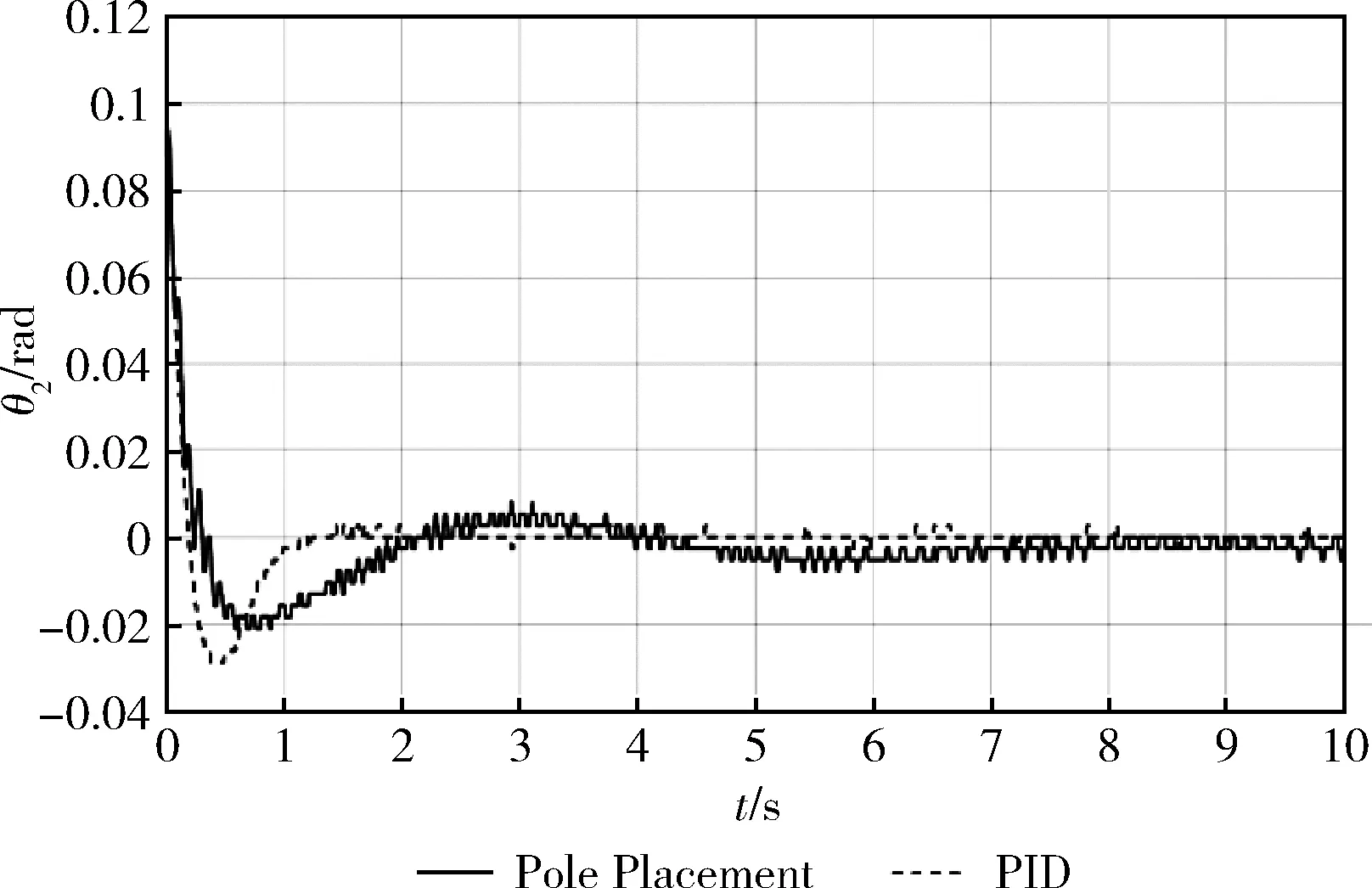
图9 环形倒立摆实验结果曲线

4 结束语

通过三维建模软件Pro/E建立环形一级倒立摆三维模型，配合Matlab插件搭建了基于SimMechanics的物理模型，并在Simulink中建立了环形倒立摆控制仿真平台，通过PID控制和极点配置法两种控制算法进行仿真，得到了较好的仿真效果。配合仿真参数，在相同的控制条件下进行了实时控制实验，实验结果与仿真数据基本一致，达到了预期效果。

仿真和实验结果表明，利用ProE/SimMechanics建模方法可以解决复杂模型的建模问题，缩短建模时间、提高建模质量，而且模型参数修改简单方便，使研究人员更能专注于控制算法研究，并在仿真过程中可以直观地看到动态效果，为机械系统建模、仿真和控制以及控制算法验证都提供了一种很便利的工具。