改进Kmeans算法的海洋数据异常检测

蒋 华，季 丰，王慧娇，王 鑫，罗一迪

(桂林电子科技大学 计算机与信息安全学院，广西 桂林 541000)

0 引 言

近十几年来我国海洋监测领域有了长足发展，获取了大量Argo浮标监测数据。但是据Argo资料的应用研究显示，Argo浮标由于自身所携带的电导率传感器，在运行过程中由于系统漂移而导致出现错误的监测数据，需要在海洋Argo浮标监测数据处理过程中尽可能的将异常数据剔除。

在“无监督学习”(unsupervised learning)中，Kmeans算法是应用最广研究最多的聚类算法之一。研究者们在传统Kmeans基础上提出了许多改进算法，如MinMaxKmeans算法[1]、KMOR算法[2]、Seeded-KMeans[3]和IWO-KMeans算法[4]等，聚类效果相较于传统算法有了明显改善，在此基础上进行的异常值检效率也更高。文献[5-10]提出了K模式聚类的两种不同的初始化算法，但不能保证初始中心点均匀分布，且算法复杂度较高。文献[11-13]提出了3种分阶段聚类方法，但时间复杂度高，人为设置约束信息使聚类变成有监督聚类。聚类和异常检测[14,15]作为数据挖掘的两个重要研究方向，可以很自然地结合起来共同研究。

为解决海洋Argo浮标数据中存在异常值问题，第一步，提出DMKmeans算法，通过计算给定邻域范围内数据点密度值，按密度值大小降序排列数据集，剔除低于平均密度值的数据点。排除密度稀疏点，在剩下的数据点中选取初始聚类中心点。第二步，基于DMKmeans算法对海洋监测数据进行异常检测研究，根据数据点距离所在簇簇心的最近距离与平均距离比较，结合数学模型来判断异常点。DMKmeans算法优化了传统Kmeans算法选取初始中心点的方法，降低了聚类迭代次数并达到全局最优结果，有效提高海洋监测数据异常检测率。

1 相关理论研究

1.1 传统Kmeans算法

传统的Kmeans算法是“无监督学习”算法，即对未标记的数据集进行聚类分析。算法思想：首先随机选取k个初始聚类中心，每一个聚类中心代表一类数据集簇；然后将数据点划分到最近的数据簇；重新计算数据簇中心点，直到聚类准则函数收敛。收敛函数定义请参见文献[15]，函数如下

(1)

式中：E为Kmeans算法针对样本D={x1,x2,…,xk}聚类所得簇C={C1,C2,…,Ck}划分的最小化平方误差，ui表示为

(2)

式中：ui是簇Ci的均值向量。直观来看，式(1)在一定程度上刻画了簇内样本围绕簇均值向量的紧密程度，通常E值越小则簇内样本相似度越高。

Kmeans算法描述见表1。

表1 Kmeans算法描述

传统的Kmeans算法对于大量数据集聚类有一定的效果，是研究者广泛研究的聚类算法之一，仍然存在初始聚类中心点的随机选定造成聚类结果局部最优问题。

1.2 密度分布函数

在数据空间Rd中，存在数据对象x和x′，数据点x′对数据点x的影响函数定义为DensityB(x,x′)，本质上该影响函数由两个数据点之间的距离决定，如欧氏距离函数。高斯函数是经典的影响函数，其定义如下

(3)

而数据点x的密度函数则是邻域参数δ范围内所有最近邻居对其影响函数之和，即若给定n个数据对象X=(x1,x2,…,xn)对于数据点x的密度函数可定义如下

(4)

式中：xi∈X,d(x,xi)为数据点x到其第i个最近邻点的最小距离，直观的通过密度函数式(3)可以看出d(x,xi)值越小Density(x)的值越大则数据点x的密度越大。

1.3 贝塞尔公式

贝塞尔公式是常用的标准偏差δ估计方法，在实际应用常常是对有限的数据样本量做标准偏差估计，但由于它并不是一个总体的标准偏差而只是一个近似估计值，因此用s表示

(5)

1.4 拉伊达准则

在整理聚类结果数据时，往往会发现总有一些数据会存在偏差较大或者分布较为突出的数据，这些数据很可能是异常值(Outliers)或噪音数据，拉伊达准则主要用以判别这些数据是否异常值从而可以决定是否保留这些数据。若存在一组聚簇样本D=(x1,x2,…,xn)，算出其在某一准则如距离簇心最近距离下的平均值x以及待检测数据元素的值xv，若是能够符合下列关系

Tabn=|xv-x|≥3s

(6)

则判断其为异常值点，其中s值为该样本的标准偏差估计，可通过式(5)计算得出。

2 基于DMKmeans算法的异常检测

2.1 DMKmeans算法

在本文的第二部分相关理论研究中，对传统Kmeans算法进行深入研究，该算法快速简单容易实现，对于大量数据集有较好的聚类效果，自行优化迭代次数比较适合大型数据集等优点。但同时也存在一些缺点，最主要的是初始聚类中心的随机选择可能使聚类效果受到离群数据的影响，造成聚类结果的局部最优而非全局最优。针对Kmeans算法的这些不足提出了DMKmeans算法，计算Rd空间上数据集X中的每一个数据点x在给定邻域半径δ范围内的最近邻居点集合G(x)，计算数据点x的密度函数Density(x)得到其密度值，并且按照升序放入集合X′中，剔除密度值小于平均密度值的数据点，从集合X′中选出密度值最大的数据点为聚类中心点，以选定的初始聚类中心点开始聚类，这样聚类结果相对稳定并可以保证全局最优。

DMKmeans算法步骤如下：

(1)在空间Rd上的数据集X={x1,x2,…,xn}中的每一个数据点xi,其中xi∈X，计算其在给定邻域半径δ内的最近邻集合Gk(xi)，即d(xi,xj)≤δ且xj∈Gk(xi)，其中k为xi在邻域范围内最近邻数据点个数；

(2)计算数据点xi的密度函数值

(7)

式中：xj∈Gk(xi)，当xi在邻域范围内的最近邻点xij的密度值小于平均密度值时，即满足下列条件

(8)

则将数据点xij视为稀疏数据并剔除掉，从而得到密集点集合X′；

(3)从密集点集合X′中，选取密度值最大的点Densitymax(x)，为第一个初始聚类中心C1；然后取距离C1最远的数据点作为第二个聚类中心C2；对于第s个中心点的选取则是满足如下条件的数据点xs且xs∈X′，取满足xs与以选中的聚类中心Cs的距离值最小的数据点作为中心点，即max(dmin(xs,C1),dmin(xs,C2),…,dmin(xs,Cs-1))其中3≤s≤k，直到最终得到所需k个初始聚类中心点，并代表k个类簇ωl,l∈(1,…,k)；

(4)计算数据集X中数据点xi至各个聚类中心点的欧氏距离

(9)

式中：i=1,2,…,n且j=1,2,…,k；如果d(xi,Cj)为最小距离值，则将数据点xi归入中心点Cj所代表的数据簇ωj中，重复该过程直到最终聚类完成；

DMKmeans算法，使用密度函数来计算出数据集中各个数据点的密度值，结合最远距离原则在高密度数据集合中选取初始中心保证其均匀分布，避免噪音数据对取定初始聚类中心的影响，使聚类迭代过程从数据高密度区域出发，有效提高迭代效率，减少迭代次数。

2.2 基于DMKmeans算法的异常检测

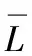
(10)

算法过程如下：

(1)设置空间Rd上的数据集X中数据点的邻域半径δ值；

(2)在空间Rd上的数据集X={x1,x2,…,xn}中的每一个数据点xi，其中xi∈X，计算其在给定邻域半径δ内的最近邻集合Gk(xi)，即d(xi,xj)≤δ且xj∈Gk(xi)，其中k为xi在邻域范围内最近邻数据点个数；

(3)据点xi的密度函数值

(11)

式中：xj∈Gk(xi)，当xi在邻域范围内的最近邻点xij的密度值小于平均密度值时，满足下列条件

(12)

则将数据点xij视为稀疏数据并剔除掉，从而得到密集点集合X′；

(4)从密集点集合X′中，选取密度值最大的点Densitymax(x)，为第一个初始聚类中心C1；然后取距离C1最远的数据点作为第二个聚类中心C2；对于第s个中心点的选取则是满足如下条件的数据点xs且xs∈X′，即max(dmin(xs,C1),dmin(xs,C2),…,dmin(xs,Cs-1))其中3≤s≤k，直到最终得到所需k个初始聚类中心点，并代表k个类簇ωl,l∈(1,…,k)；

(5)计算数据集X中数据点xi至各个聚类中心点的欧氏距离

(13)

式中：i=1,2,…,n且j=1,2,…,k；如果d(xi,Cj)为最小距离值，则将数据点xi归入中心点Cj所代表的数据簇ωj中，计算其最小化平方误差E，并对ωj中所有数据点计算距离均值从而得到新的聚类中心点；

(6)重复过程(5)直到聚类准则函数收敛，即前后两次迭代所得出式(1)中E的值的差小于等于阈值η即|E-E′|≤η，聚类中心点不再改变，至此聚类过程结束，得出聚类结果；

(7)计算最终数据簇ωp中数据点xi到簇心Cp的平均距离

(14)

(8)若待观察序列U中的数据点xa∈U到簇心的距离值da满足条件

(15)

则判定该数据点为异常点，将其保留在数据集U中，否则的话将不满足条件的数据点放回原来聚类数据簇中，重复上述过程直到最终异常值检测完成并输出异常值点。

基于DMKmeans算法的数据异常检测算法，在全局最优聚类结果基础上使用拉伊达准则，贝塞尔公式等数学模型来进行数据异常检测，异常检测率较高。

3 实验及结果分析

通过DMKmeans算法与传统Kmeans算法以及MinMaxKmeans算法的海洋监测数据仿真实验对比，验证算法的可靠性和稳定性，实验评估指标主要有运行平均时间、迭代次数、聚类准确率、异常检测率等。

实验环境：Matlab2016a、Windows7 64 bit、CUP 2.67 GHz、内存6 G。所使用数据集为海洋Argo浮标监测数据集，数据来源于中国Argo实时资料中心公开数据集。实验参数δ=0.5，K=5，η=0.01。

图1为本文所提DMKmeans算法海洋监测数据异常检测仿真实验，图2为MinMaxKmeans算法海洋监测数据异常检测仿真实验，图3为传统Kmeans算法海洋监测数据异常检测仿真实验，以上3个实验图形中均有5个聚类数据簇，其中‘+’代表检测出的异常点。与其它两种对比算法相比较，DMKmeans算法在聚类效果上聚类数据簇更加紧密清晰，类簇分布更加均匀，基于DMKmeans算法的海洋监测数据异常检测相比传统Kmeans算法以及MinMaxKmeans算法准确率更高。

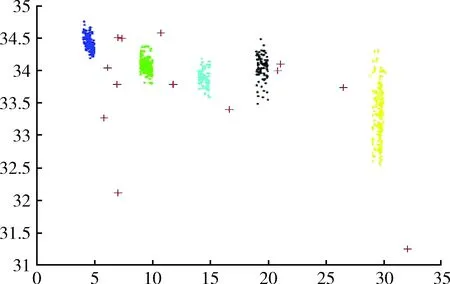
图1 DMKmeans算法异常检测

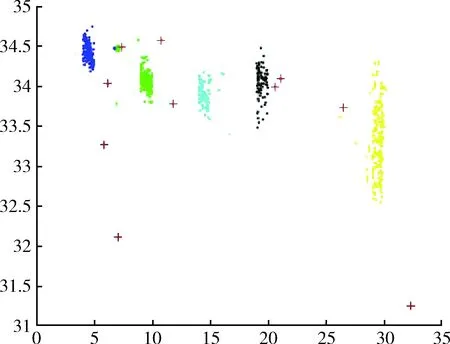
图2 MinMaxKmeans算法异常检测

图3 传统Kmeans算法异常检测

从表2、表3实验数据可以看出，本文提出的DMKmeans算法在迭代次数和聚类准确率上都优于MinMaxKmeans算法和传统Kmeans算法，在此基础之上所做的海洋监测数据异常检测仿真实验，平均运行时间比MinMaxKmeans算法以及传统Kmeans算法更短，异常检测率较其它两种算法要高。结合以上仿真实验结果和数据分析可以得出结论，DMKmeans算法比MinMaxKmeans算法以及传统Kmeans算法在聚类和异常检测方面更加优化，可以满足实际应用的需求，有助于海洋Argo浮标数据集聚类以及异常检测。

表2 聚类实验结果对比

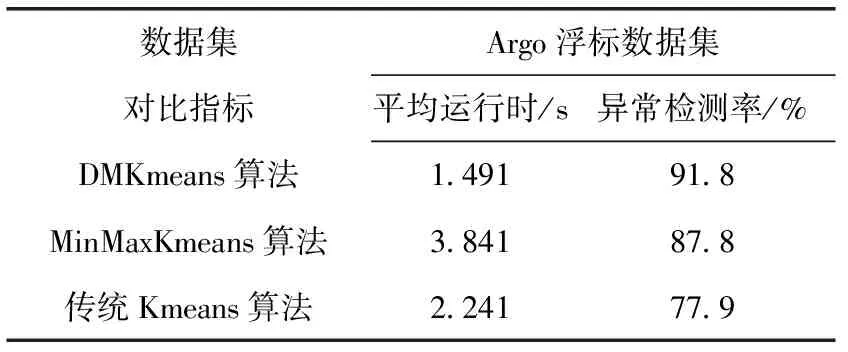
表3 异常检测实验结果对比

4 结束语

DMKmeans算法解决了传统Kmeans算法初始聚类中心随机选取造成聚类结果局部最优的问题，选择密度分布较高的数据点作为初始聚类中心可以有效排除离群点对初始聚类的干扰，初始聚类中心均匀分布，减少迭代次数，使最终聚类结果全局最优，基于DMKmeans算法的海洋监测数据异常检测可以有效检测出海洋Argo浮标数据集中的异常值。

通过DMKmeans算法与传统Kmeans算法及MinMaxKmeans算法的海洋监测数据异常检测仿真实验对比分析，DMKmeans算法在运行时间、迭代次数相比传统Kmeans算法和MinMaxKmeans算法更少，聚类速度更快，对异常数据检测更加稳定。DMKmeans算法的聚类准确率和异常检测率高于其它两种对比算法。本文提出的DMKmeans算法能更好地检测出海洋Argo浮标数据集中的异常数据。随着大数据时代到来，使用大数据平台对更加海量的数据集和高维数据集的异常检测将会成为本文下一步研究的重点。