超宽带滤波器的稀疏贝叶斯正则化逆向神经网络建模
2018-10-24南敬昌王梓琦高明明
南敬昌 王梓琦 高明明 王 颖
(辽宁工程技术大学电子与信息工程学院 辽宁 葫芦岛 125105)
0 引 言
随着无线通信的快速发展,射频微波器件扮演着关键角色,因此对其建模、仿真算法和设计分析方法等也提出了更高的要求。传统的射频微波器件设计与分析方法采用基于计算机的辅助设计方法,最常见的优化方法是EM电磁仿真软件法,但它往往需要经过长时间的优化来得到各个目标参数,计算代价较大。
神经网络具有很强的非线性逼近和优化求解能力,对于大型复杂问题能快速建模求解,在射频微波领域得到了广泛的应用[1]。通常将其对射频微波器件的建模问题归为两类:一类被训练用来模拟原始电磁问题,称为正向建模,训练好的正向神经网络能够依据器件结构参量精确地得到系统响应;另一类被训练用来设计器件,称为逆向建模,可以通过给定的目标参量综合出对应的结构参量[2-3]。
对于直接逆向神经网络,它可以通过交换网络的输入输出数据来获得,其优点是建模速度快,但是由于输入与输出参量之间的多值映射关系,难以保证其收敛性和唯一性[4]。文献[3]提出一种在训练前对数据进行分组处理的逆向建模方法,根据分组规则,消除多解问题,将各子逆模型的输出作为正向模型的输入,如果正向模型的输出与子逆模型的输入在一定的误差范围内,则按照一定规则合并,应用于波导滤波器的设计中。此方法模型分组和子模型合并的过程加大了建模的复杂度,一旦其中一步精度差,整个逆向模型的精度也较差。文献[5]则提出了对多输入模型建立一系列候选逆模型,将具有最小误差的候选逆模型作为理想逆模型与原始模型互补,得到精确逆模型的梯度逆向建模方法,并应用于传输线和螺旋电感建模中。对于正则化神经网络算法,文献[6]证明了带L2正则化项的逆向迭代算法的确定性收敛;文献[7]证明了带光滑L1/2正则化项的神经网络逆向迭代算法能保证输入向量序列在训练过程中的稳定性及稀疏性;文献[8]指出可以通过贝叶斯正则化方法来提高BP网络的泛化能力;文献[9]提出一种基于稀疏贝叶斯的半监督极速学习机分类算法,并证明了其可以避免Moore-Penrose广义逆方法求解产生的过拟合问题,具有较好的稀疏性和泛化能力。
针对以上研究现状以及已有的逆向建模方法过程复杂、模型精度难以保证、BP逆向建模方法网络泛化能力差的问题,提出一种稀疏贝叶斯正则化逆向神经网络建模方法。此方法通过L1/2范数引入新的权系数,使得网络结构更加稀疏化,并实现对输入样本的扩展,网络输出解更具稀疏性,同时通过贝叶斯正则化方法调整网络权系数避免过拟合现象,网络输出更加平滑,且泛化能力更强。以模型实际输出与目标输出之间误差的最小化为目标在输入空间内搜索全局最优解,具有唯一性。将此逆向神经网络应用于超宽带滤波器加载谐振器的建模中,可以更加精确、快速地得到其逆模型,效率更高。
1 稀疏贝叶斯正则化逆向神经网络迭代算法
1.1 正则化方法
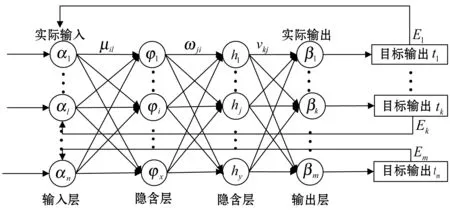
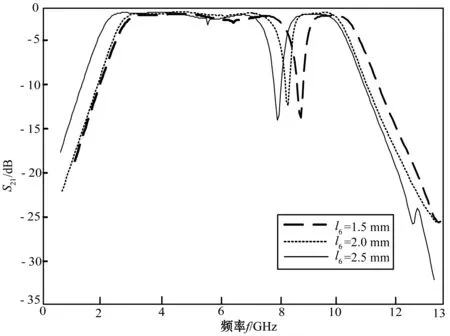
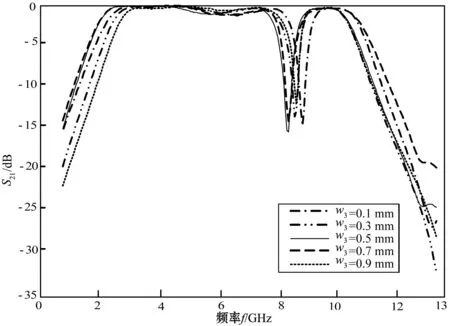
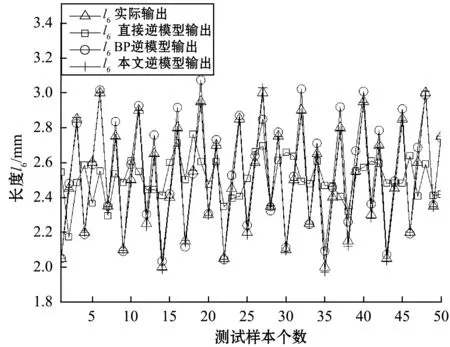
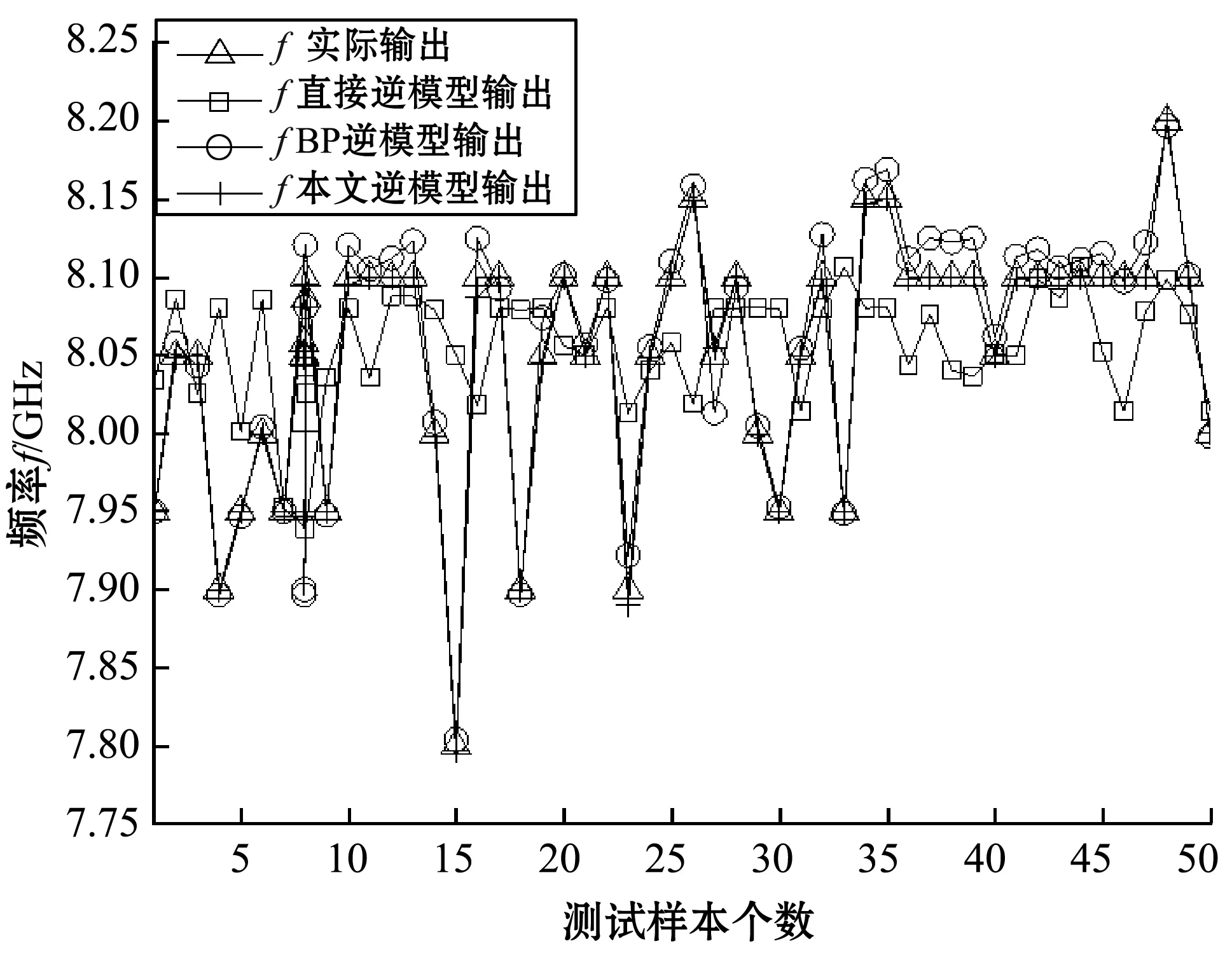
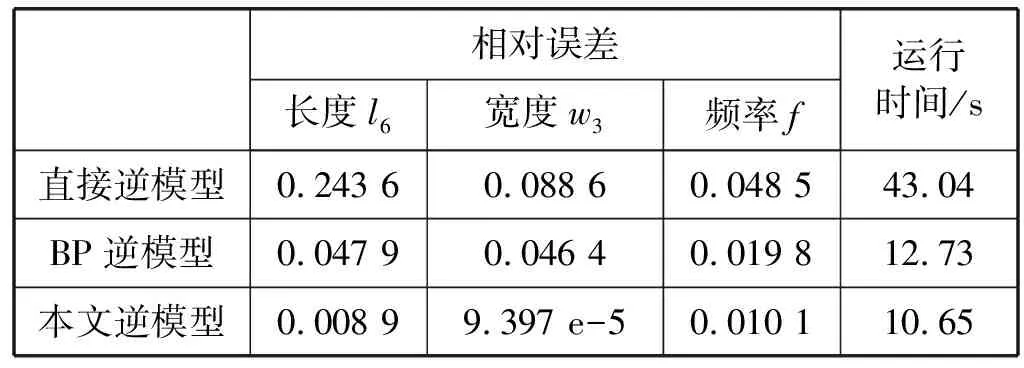
从神经网络的精度角度而言,稀疏化的研究意义在于保证精度的同时降低训练成本避免过度训练,L1/2惩罚项能够代替算法中的Lp(0 贝叶斯方法利用概率对事物进行描述,为一个随机数,用概率分布描述的大小,在未知数据时,用来描述的概率分布情况称为先验概率分布。贝叶斯公式为: (1) 当样本x出现后,人们对进行调整,π(θ|x)即为对应的后验分布[14]。 这里采用典型的具有一个输入层,两个隐含层和一个输出层的逆向神经网络结构,如图1所示。 图1 逆向神经网络结构图 其中α=(α1,…,αl,…,αn)是输入向量,β=(β1,…,βk,…,βm)是输出向量,μil是输入层第l个神经元和隐含层第i个神经元之间的权值,ωji是隐含层第i个神经元到隐含层第j个神经元的权值,vkj是隐含层第j个神经元到输出层第k个神经元之间的权值;φiq为第一个隐含层第i个神经元输出,hjq为第二个隐含层第j个神经元输出,E是目标输出向量t与实际输出向量β之间的误差函数,其中传递函数采用tansig函数T(·),T(·)的导数为T′=1-T2。因此,神经网络输出按下式计算: βk(rl)=2/(1+exp(-2×(rl)))-1 (2) 式中,rl是加权输入。神经网络的相对误差函数Eq可以描述为: (3) 式中:N为样本总数,q表示第q组测试数据,Eq代表第q组数据的误差,tkq表示第q组第k个目标输出向量。常规的贝叶斯正则化方法是在误差函数后加上权衰减项: (4) 因此,本文提出的稀疏贝叶斯正则化神经网络的性能函数描述为: (5) 通过贝叶斯正则化方法可以在网络训练过程中调整正则化系数λ的大小,自动缩小网络规模,使模型网络输出更加平滑[14]。增加L1/2范数,引入新的权值向量,使得网络结构更加稀疏化,同时在逆向迭代性能函数中实现对输入向量扩展,使得模型可以得到具稀疏性的解,提高了网络泛化能力。 不同于正向建模中改变网络的权值,神经网络逆模型的误差是由输入参量引起的,因此需要不断修正输入参量的值。更新后的输入参量使得实际输出与目标输出之间的误差最小,可描述为: (6) 式中:η>0为学习速率。 为了求得稀疏贝叶斯正则化神经网络的逆向迭代算法,需要求解式(5)性能函数关于输入参量α的导数,因此将其分解为以下两项: (7) (8) 第一个隐含层第i个神经元输出值φiq可由下式计算: (9) φiq对第l个输入值αlq的偏导为: (10) 同样可求,第二个隐含层的第j个输出值hjq对输入值φiq的偏导为: (11) 隐含层输出hjq对输入值αlq的偏导为: (12) 同理,第k个输出值βkq对hjq的偏导为: (13) 误差函数Exq对于输入参量αlq的偏导为: (14) 设式(14)中的第一个因子如式(15): (15) 将式(12)、式(13)、式(15)代入式(14)可得: (16) 误差函数Eyq关于输入参量αlq的偏导为: (17) 式中:sgn(·)为符号函数。 因此,由式(16)、式(17)可得: (18) 将式(18)代入式(6)中,对输入参量迭代更新,实现逆向求解过程。 对于神经网络逆向建模,如图2所示。具体步骤如下: 1) 利用EM电磁仿真或从实物中获取实验数据,分为训练集和测试集。 2) 对数据进行归一化处理,利用训练数据训练神经网络正模型,获得权值并保存。 3) 代入正向网络获得的权值,利用本文提出的稀疏贝叶斯正则化神经网络逆向迭代算法更新输入参量α,实现逆向求解过程。 4) 若达到性能函数E要求或最大迭代次数,则结束更新。最后以实际输入和目标输入之间的误差大小来评价模型性能的好坏。 采用三维电磁仿真软件Ansoft HFSS 13.0建立加载谐振器的超宽带滤波器模型[15-16]。超宽带滤波器结构如图3所示。 图3 加载谐振器的超宽带滤波器 图3中的超宽带滤波器在选择结构支节的尺寸时,经计算与优化,耦合线的长度l1,耦合线之间的距离w1,谐振器的宽度w2,谐振器长度为l2的值初步确定。主要需要考虑其加载的谐振器在陷波中心频率f处,长度l6、宽度w3(单位:mm)对滤波器插入损耗S21的影响。在Ansoft HFSS 13.0中所建模型如图4所示。 图4 超宽带滤波器HFSS模型 图5为在HFSS中保持支节l1-l5和宽度w不变,对支节l6分别取1.5 mm、2.0 mm、2.5 mm时的扫描结果,随着l6的增大,陷波的中心频率逐渐左移,插入损耗S21也随之改变。同样,保持支节l及宽度w1、w2的值不变,w3取值分别为0.1 mm、0.3 mm、0.5 mm、0.7 mm、0.9 mm时,扫描结果如图6所示,陷波中心频率和插入损耗S21也随之改变。 图5 长度l6与S21的关系 图6 宽度w3与S21的关系 利用图4根据超宽带滤波器的插入损耗S21随谐振器结构参数变化时的仿真结果,提取1 200组数据用于训练和测试,其中l6取值范围为:2~3 mm,间隔为:0.05 mm;w3取值范围为0.3~0.7 mm,间隔为0.02 mm;对应的f取值范围为7.8~8.4 GHz,S21范围为10.8~16.4。 对于不同的l6和w3与S21之间关系如图7所示。可以看到一个S21分别与多个l6值和多个w3值相对应,当把已知S21作为输入,会有多个l6和w3值与其对应,即存在多解问题。 图7 S21与l6和w3的对应关系 在使用HFSS软件进行优化的过程中,需要不断调整谐振器在陷波中心频率处的结构尺寸来得到理想S21的值,需要花费大量时间,增加了设计代价。为了能够快速地通过目标插入损耗S21的值逆向求解陷波中心频率f处的结构参量长度l6、宽度w3的值,采用本文提出的稀疏贝叶斯正则化逆向神经网络建模方法对此超宽带滤波器进行建模。 在MATLAB 13.0软件中编程实现稀疏贝叶斯正则化神经网络逆向迭代算法,选择1 000组作为训练数据,50组作为测试数据。 为了加快学习训练速率,首先对所需数据进行归一化处理,使量纲保持一致。本文采用min-max标准归一化方法: (19) 式中:α*∈Rn,αmin=min(α),αmsx=max(α)。 根据实验情况,此逆模型采用4层神经网络结构,确定各层节点数为3-23-20-1,输入层三个节点,分别为l6、w3、f,输出层一个节点,为S21,误差限设为1e-6,最大迭代次数为500,通过仿真模拟发现当学习速率η取0.02,正则化系数λ取0.68时,误差最小。 采用本文所提的逆向建模方法对超宽带滤波器进行建模,模型输出结果分别与电磁仿真软件HFSS实际输出、直接逆向建模方法输出和BP逆向建模方法输出进行对比,三种方法采用相同的网络结构,对比结果如图8-图10所示。 图8 长度l6拟合图 图9 宽度w3拟合图 图10 频率f拟合图 从图8-图10可以看出由于多解问题的存在,直接逆模型的拟合效果较差,而本文提出的逆向建模算法所得结果可以较好地拟合电磁仿真结果,模型精度较高。 直接逆模型、BP逆模型与本文逆模型网络输出的对比结果如表1所示。与BP逆向建模方法相比,本文逆模型求得的与插入损耗S21对应的长度l6、宽度w3、频率f的相对误差分别减小了81.4%、99.8%、48.9%,网络运行时间减少了16.3%。 表1 三种逆向建模方法仿真结果对比 将稀疏贝叶斯正则化逆向神经网络应用于超宽带滤波器的建模中,通过目标电参量能够快速综合出对应的结构参量。L1/2范数使得逆模型更易得到稀疏性解,贝叶斯正则化方法调整网络权系数,可以有效避免过拟合现象,网络泛化能力及稀疏性更好。此逆向神经网络通过迭代过程取代了连续搜索的程序优化方法,不存在多解问题,与直接逆向建模方法和BP逆建模方法相比,此逆向建模方法更加准确和高效。1.2 稀疏贝叶斯正则化性能函数
1.3 稀疏贝叶斯正则化逆向神经网络算法推导
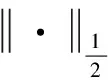
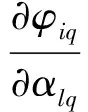
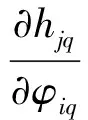
2 神经网络逆向建模过程
3 超宽带滤波器的逆向神经网络建模
3.1 超宽带滤波器模型


3.2 关键参数提取

3.3 超宽带滤波器的稀疏贝叶斯正则化逆向神经网络建模
4 仿真结果分析

5 结 语
