基于信息熵加权的FCM交通状态识别研究

曹 洁 张丽君 侯 亮 陈作汉 张 红

1(兰州理工大学计算机与通信学院 甘肃 兰州 730050)2(甘肃省制造业信息化工程研究中心 甘肃 兰州 730050)

0 引 言

如何准确地对城市路网的交通状态进行识别是智能交通(ITS)的重要研究内容之一[1]。该内容在出行者信息系统(TIS)和交通管理系统(TMS)等ITS子系统中应用较广泛[2]。通过对路网交通状态的识别，可以从全局角度实时反映交通流总体运行状态，对交通控制和交通诱导起着先导作用。

由于交通状态的特性是具有模糊性和不确定性[3]，通常可使用一些交通数据对其变化情况进行定量的说明及反馈。而聚类分析作为一种无监督机器学习算法，能够在没有任何先验知识的情况下实现交通流数据的模式分类[4]。因此，该算法在交通状态识别领域中受到广泛应用。文献[5]在感应线圈所采集到的交通数据基础上，提出一种基于模糊聚类的交通状态判别算法及评价方法；文献[6]结合高速公路拥堵的特点，建立了基于FCM粗糙集的城市高速公路交通状态识别模型。以上方法虽然能够快速识别高速路段和城市路段的交通状态，但对交通流在交叉口处的间断性与复杂性考虑得不够全面。文献[7]通过分析交通流的特征并对交通状态进行划分，提出一种基于FCM聚类算法实时识别交通状态的方法；文献[8]基于大数据驱动技术并结合FCM聚类算法构建了一种交通状态聚类模型。以上方法虽然实现了交通状态的快速识别，但对评价指标在交通状态识别结果中的权重影响问题考虑得不够全面。文献[9]将交通流的3个参数(流量、速度、占有率)作为样本数据的评价指标，提出基于FCM聚类算法的交通状态实时判别方法；文献[10]在FCM聚类算法的基础上，通过设定交通评价指标的权重，提出基于不同参数权重的交通状态识别方法。以上方法虽然根据评价指标的权重对交通状态进行了识别，但对评价指标权重的确定具有一定的主观性，影响到最终的识别结果。

针对以上问题，本文将路网中关键交叉口和其上游路段作为一个交通状态识别单元，引入概率论中的信息熵确定每个评价指标的权重，提出基于信息熵加权的FCM聚类交通状态识别方法。利用理论分析与实验仿真验证本文所提出方法的有效性。

1 交通状态识别与FCM算法

交通状态识别是解决交通拥堵问题的首要任务。其步骤如下：首先，选取路网中关键交叉口和其上游路段作为交通状态识别单元并采集该识别单元的交通数据；其次，根据不同交通状态的交通评价指标阈值不同，利用信息熵对选取的评价指标进行权重计算，以解决评价指标对交通状态影响程度不同的问题；最后，利用改进FCM算法对采集的交通数据进行仿真，输出交通状态的聚类结果。整个流程如图1所示。

图1 交通状态识别流程图

1.1 识别单元的建立与状态划分

传统交通状态的识别单元是单一交叉口或单一路段，但在城市路网中由于交叉口的交通供给不足，会影响到上游路段的通行能力[11]。因此，为了有效地度量路网的交通状态，本文将路网中关键交叉口和其上游路段作为交通状态识别的单元，如图2所示。

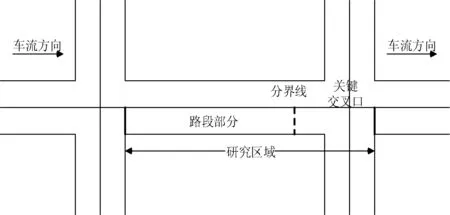
图2 交通状态判别的研究区域

交叉口的不同交通状态会引起车辆的排队长度不同[12]，具体表现为：当交叉口畅通时，车辆可能需要一个绿灯时间通过交叉口，此时排队长度为该时间内通过的车辆数；当交叉口严重拥堵时，车辆可能需要两个或两个以上的绿灯时间通过交叉口，此时排队长度为多个绿灯时间通过的车辆数。因此，本文选取交叉口评价指标(饱和度、排队长度)和其上游路段评价指标(平均行程速度、时间占有率)来进行交通状态的准确识别。

为了确定以上4种交通状态识别指标的阈值，本文将《交通工程学》、《城市道路交通管理评价指标体系》与国内城市交通状态的研究相结合，得出的结果如表1所示。

表1 交通状态识别指标阈值

1.2 FCM聚类算法

模糊C均值FCM(Fuzzy C-means)的原理是将聚类定义为一个约束的非线性规划问题，并通过不断迭代优化使其目标函数取得最小值，实现样本数据集的划分和聚类[13]。

假定一个数据样本集为X={x1,x2,…,xn}，每个样本xi有m个评价指标，即xi={xi1,xi2,…,xim}。其中，样本集X的一个子集为模糊簇集V1,V2,…,Vc。FCM的目标函数为：

(1)

式中：各个数据样本与相应聚类中心隶属度构成的隶属度矩阵为U；聚类中心矩阵为V；样本数据矩阵为X；第j个数据样本的第i个聚类中心隶属度为uij；q是一个隶属度的因子，表示属于样本的轻缓程度；第i个聚类中心到第j个数据样本的欧式距离为dij，定义如下：

(2)

1) 随机初始化uij。随机地选取q值，同时对于每个点xi和每个簇Vj，隶属度uij取0和1之间的值。为了形成合理的模糊伪划分，uij满足约束条件：

(3)

2) 计算质心。对于簇Vj，对应的质心vj由下式定义：

(4)

3) 更新模糊伪划分。

(5)

FCM算法不断重复地计算每个簇的质心和模糊伪划分，直到划分达到稳定状态(迭代终止条件为“所有uij变化的绝对值低于指定的阈值”)。

2 改进方法

2.1 信息熵加权

在传统交通状态的识别方法中，将不同评价指标的权重视为相等或主观确定其大小，从而影响到识别的准确性。为了解决该问题，本文引入概率论中的信息熵来确定不同交通评价指标的权重。

信息熵的实质是对系统无序程度的一种度量方式[14]，其度量准则为：信息熵越大，系统的无序程度越高，提供的信息就越少[15]。从信息论与交通状态相结合的角度来看，各个评价指标权重的熵值并不是为了评价该指标的实际熵值(信息量)大小，而是体现其在交通状态识别中提供有用信息的多少，反映每个评价指标的相对重要性。基于此,本文计算交通评价指标权重的过程如下：

1) 通过评价指标的阈值表，建立交通状态识别系统的评价矩阵：

(6)

式中：需要识别的交通状态有c(c=4)种类别，m(m=4)个交通评价指标，xij为第i类交通状态的第j个交通评价指标的阈值。

2) 对评价矩阵X进行归一化处理。为了解决交通指标量纲不同的问题，用以下公式对矩阵X进行归一化处理：

(7)

3) 计算熵值。交通状态类别关于各个属性指标j的熵值为：

(8)

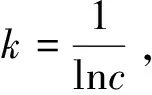
4) 计算评价指标的偏差度。第dj=1-Ej,j=1,2,…,m个交通评价指标的偏差度为：

dj=1-Ejj=1,2,…,m

(9)

5) 计算每个交通评价指标的权重大小。用熵测度来表示第j个指标的权重系数为：

(10)

式中：第j个交通评价指标rij(j=1,2,…,m)值的分布情况可以衡量该指标对交通状态的影响程度。其衡量准则为：rij值分布越分散，相应的dj值越大，该指标对交通状态的影响程度越高；相反，rij值分布越集中，相应的dj值越小，该评价指标对交通状态的影响程度越低。

6) 确定分类样本的特性指标矩阵。设有n个交通状态识别单元，样本集为X={x1,x2,…,xn}，每个xi有m个评价指标，利用信息熵确定每个特性指标的权重大小，即n个待分类样本的特性指标矩阵为：

(11)

当交通特性指标选取m(m=4)时，上述矩阵的列分别是饱和度、平均排队长度，平均行程速度和时间占有率；矩阵的行代表识别单元样本。

通过信息熵理论对表1中交通状态评价指标的权重进行计算，得出以上4个评价指标的权重向量为W={w1,w2,w3,w4}={0.128 4,0.301 8,0.188 4,0.381 4}。

2.2 加权的FCM聚类算法

引入信息熵确定出各个指标的权重后，通过计算误差的平方和来确定每个样本数据和类中心间距最小的隶属度矩阵以及c个聚类中心，改进的FCM算法的目标函数定义如下：

(12)

(13)

本文通过信息熵理论对交通状态指标进行权重的计算，并采用加权的欧氏距离来优化FCM聚类算法的目标函数，最后，通过改进算法对城市路网的交通数据进行聚类仿真。具体实现步骤如下：

Step2根据交通数据的性质，对模糊参数q和迭代停止阈值ε进行设置；

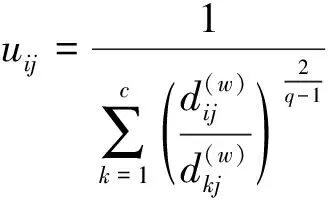
Step5当‖V(l+1)-V(l)‖≤ε时，则算法终止。此时，V*=V(l+1)为最终所求聚类中心；否则，令l=l+1，返回Step3继续迭代。

3 实验与分析

3.1 实验数据采集

为了验证改进后FCM算法的有效性，选择城市局部路网的实测数据进行交通状态识别仿真，路网如图3所示。

图3 路网结构图

将路网中关键交叉口A3和其上游路段作为交通状态的识别单元，对其进行数据采集。数据采集时间为工作日上午6:00-11:45(70组/天，共350组)，时间间隔为5 min，每组数据样本包括状态识别单元的4个评价指标(饱和度、平均排队长度、平均行程速度和时间占有率)。通过MATLAB平台对采集的交通样本数据进行畅通、稳定、一般拥堵和严重拥堵四种状态的聚类仿真。根据样本数据的性质，本文选取模糊指数q=2.25[16]，迭代终止阈值ε为0.01。

3.2 改进前后聚类结果的比较

实验选取其中一个工作日的70组交通数据，分别输入到改进前后的FCM聚类算法中，得出4种交通状态的聚类中心矩阵。

1) 传统FCM算法的聚类中心矩阵：

2) 加权后FCM算法的聚类中心矩阵：

上述聚类中心矩阵中，列表示一类交通状态的4个评价指标，行表示一个评价指标在4种交通状态下的值，且矩阵元素与交通状态参数的阈值相符合。

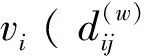
通过对路网采集的数据集进行实验仿真，得到改进前后算法的隶属度函数如图4所示。

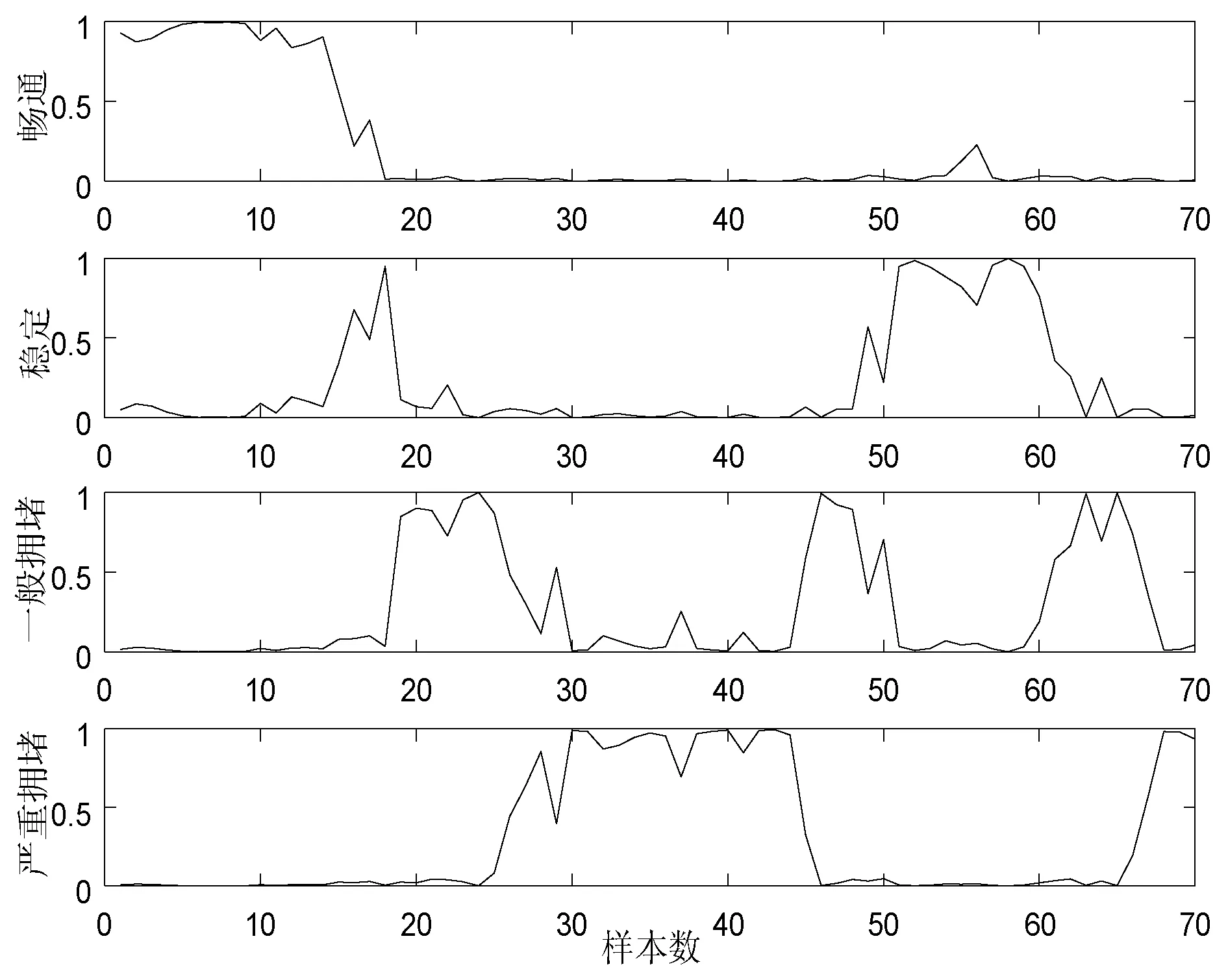
(a) 改进前算法的隶属度函数

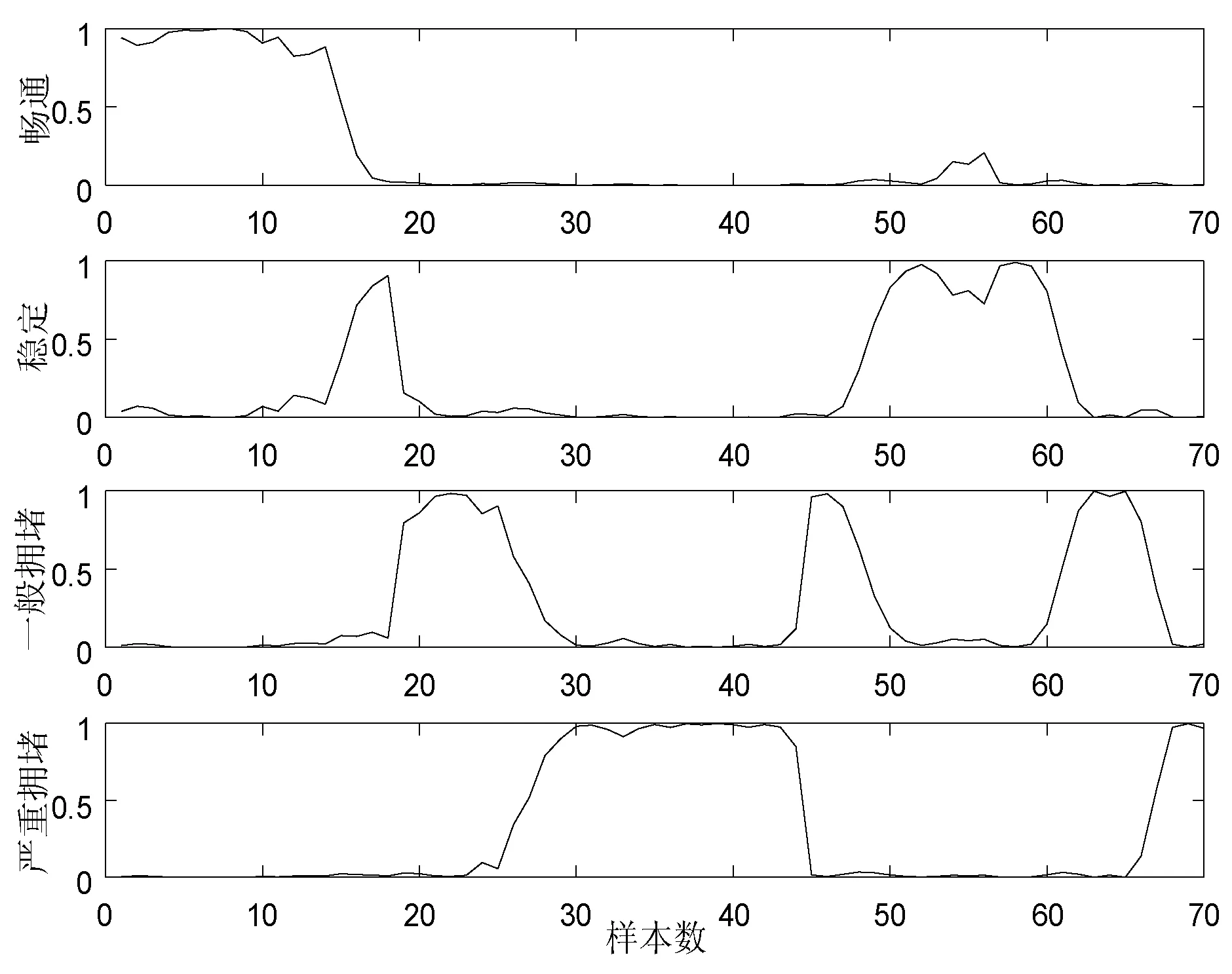
(b) 改进后算法的隶属度函数图4 改进前后算法的隶属度函数

由图4可知：(1) 改进后算法的隶属度函数在四类交通状态的曲线较改进前更加平滑；(2) 改进后算法的隶属度函数在四类交通状态的值较改进前接近于1的样本数有所增多。实验结果表明：基于信息熵加权改进的FCM算法聚类效果更佳，分类性能提高。

FCM算法的目标函数由相应样本的隶属度值与该样本到各个交通状态聚类中心的距离相乘组成的。衡量算法聚类中心能否准确表示各个交通状态中心的指标是算法产生的目标函数。其衡量准则为：聚类产生的目标函数值越小，聚类中心越能更好地代表各个交通状态的中心。

通过对路网采集的数据集进行实验仿真，得到改进前后算法的目标函数如图5所示。

图5 改进前后算法的目标函数

由图5可知，在第一次迭代时，改进后算法的目标函数值(约630)远远小于改进前算法的目标函数值(1 000)。在迭代过程中，两种算法的目标函数都在持续减小，但改进后算法达到目标函数最小值的迭代次数(10次)小于改进前算法达到目标函数最小值的迭代次数(15次)。迭代完成时，改进后算法目标函数的最小值(约100)小于改进前算法目标函数的最小值(约160)，降低了约37.5%。实验结果表明：基于信息熵加权改进的算法以更少的迭代次数达到更小的目标函数值，改进算法的效率和性能有所提高。

3.3 改进前后识别率的比较

本文所选取路网的关键交叉口靠近公交车站且车流量较大，根据视频检测器中对交通状态的判断，得出该工作日在采集时间段内的实际路网交通状态为：畅通(6:00-7:05)，稳定状态(7:05-7:25)，一般拥堵状态(7:25-8:00)，严重拥堵状态(8:00-9:40)，一般拥堵状态(9:40-10:05)，稳定状态(10:05-11:00)，一般拥堵状态(11:00-11:30)，严重拥堵状态(11:30-11:45)。

在交通状态的隶属度波形图(图4)中，将样本隶属度值最大所对应的交通状态定义为该样本的交通状态。通过对采集时间段内路网的实际交通状态与算法改进前后识别的交通状态进行对比，得出如图6所示的结果。其中，交通状态的等级分别为1-畅通、2-稳定、3-一般拥堵及4-严重拥堵。

图6 实际状态与改进前后识别状态

由图6可知，改进前FCM聚类算法对交通状态识别不准确的时间段分别是8:25-9:45和9:50-10:05。改进后FCM聚类算法对交通状态识别不准确的时间段是9:55-10:05。实验结果表明，改进后算法识别不准确的时间段较少，更接近于实际的交通状态。

为了进一步明确改进算法的识别率大小，将隶属度值在0.5～1之间且符合实际交通状态的数据样本视为正确识别的样本。表2是改进前后算法对5个工作日采集的所有数据(350组)的聚类结果。

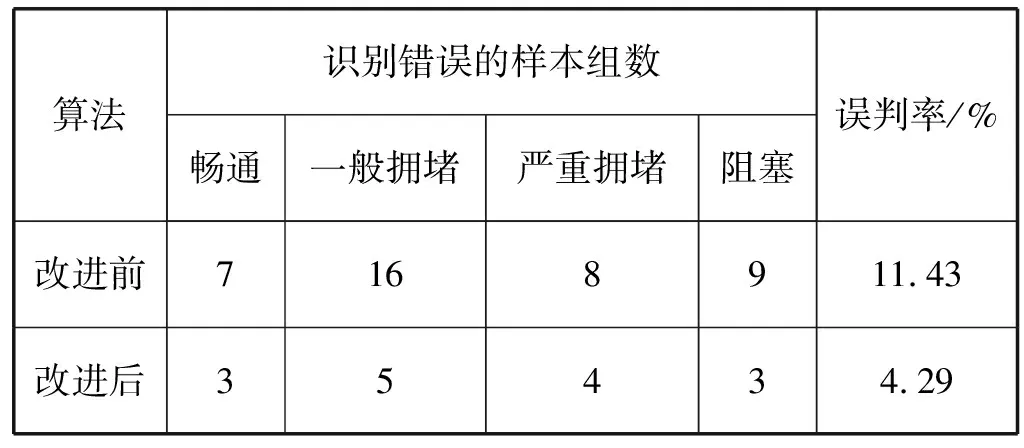
表2 聚类结果分析

由表2可知：文中采用信息熵理论对识别指标进行权重计算，相比于传统FCM聚类算法，改进后算法识别错误的样本总组数少于改进前识别错误的样本组数，误判率降低了7.14%。实验结果表明，文中改进的聚类算法是有效的，避免了因主观确定权重而造成识别不准确的后果。

4 结 语

本文在传统FCM聚类算法的基础上，考虑到评价指标对交通状态的影响程度不同，采用信息熵理论计算交通状态评判指标的权重，提出了一种基于加权的FCM聚类算法的交通状态识别方法。通过采集城市局部路网的交通数据，并用改进前后的算法进行仿真，实验结果表明，改进后的聚类算法能有效识别路网的交通状态。但聚类中心个数的选取会影响到算法的性能，因此，下一步将致力于其个数的优选研究。