在“思辨”中发展立体几何思维的严密性——以“线面平行的判定”为例

☉江苏省徐州市第二中学 马姗姗

新课改后，立体几何定位于培养和发展学生的几何直观能力、空间想象能力和推理论证能力等，淡化了对几何严格证明的要求，但数学是一门以严谨著称的学科，那么缺失了严格证明的立体几何教学，其严密性如何保障，如何让学生真正理解立体几何中的重要定理、性质？这就需要在教学中强化“思辨”能力的作用.思辨能力顾名思义就是思考辨析能力，即通过分析、推理、判断等思维活动对事物的情况、类别、事理等的辨别分析.下面笔者就以“线面平行的判定”一课为例，谈谈对此的看法.

一、结合生活现实，“思辨”解决方案

我们生活的世界不仅被形形色色的几何现象与模型所包围，大到高楼大厦、公路桥梁，小到橡皮铅笔、螺丝尺具，而且很多生活问题本质上就是立体几何问题，通过对生活问题的“思辨”，我们能够获得蕴藏在其中几何原理.比如，木工用一把直尺在桌面上随处置放，如果尺上有两点在桌面上，而有其他不在桌面上，则就说明桌面不平整，否则桌面就是平的；在装箱子的盖子时，用到两块铰链与一把锁，从而把盖子固定在箱子上.上述两个例子就蕴含着立体几何的两大公理.不仅如此，现行教材的编写也是遵循从“生活模型中发现”的思路，空间中的位置关系基本上都是从生活实例中提炼出来的.因此，结合生活现实进行“思辨”是立体几何教学的第一步，它有助于明确问题的解决方案.

师：如何保证教室里所安装的日光灯与地面平行？

生1：测量一下日光灯两端到地面的距离，看它们的长度是否一样.（根据生活经验，学生很快想到了办法）

生2：只要保证日光灯两端的绳子的长度一样就行.

师：我们发现教室里的日光灯确实是这样安装的，那你能把这个实际问题转化为数学问题吗？其中蕴含着什么数学原理？

生3：这就是线面平行问题，通过这个现象，我们可以得到一个结论：如果直线上有两点到平面的距离相等，则这条直线与平面平行.

师：你们认为这个结论在空间中成立吗？

生4：不成立，如果直线与平面相交，照样可以找到两点到平面的距离相等.

师：为什么在生活中是正确的经验，到了数学中就不对了呢？

生5：因为直线可以无限延伸，而日光灯的长度是有限的.

师：那在空间中如何判定线面平行呢？如果直线上有三个点到平面距离相等，你认为能否判定直线与平面是否平行？

生6：好像也不对.如果直线在平面内，那么直线上有无数个点到平面的距离相等.

师：那如何改进判定方法呢？

生7：“平面外”的一条直线有三个点到平面的距离相等，则直线与平面平行.

当学生对空间图形认识不清时，基于错误的空间认识进行推理就会得到错误的结论.借助现实的具体模型与生活现象进行“思辨”，不仅有利于促进学生对于空间问题的理解，而且有利于架起学生的生活经验与数学原理联系的桥梁.通过不断的“尝试”，不断的“思辨”，学生逐步明确了解决问题的方案.

二、联系已有经验，“思辨”论证方向

建构主义认为，知识不能简单地由教师进行“复制”再“粘贴”到学生的头脑中，而只能是每个学生依据已有的知识和经验主动地加以建构的过程.学生已有的经验是课堂教学的“出发点”，也是知识的“生长点”，这在立体几何“公理化”的论证思想中体现的淋漓尽致.所谓“公理”是“人们普遍认为正确的结论”，毫无疑问，公理依赖于“经验”，从公理出发通过演绎证明从而获得新的定理、性质、推论.其论证思想也可以直接理解为从“已有的经验”出发获得更多的“新的经验”.

师：刚才有同学提出“‘平面外’的一条直线有三个点到平面的距离相等，则直线与平面平行”.这个结论正确吗？

生：正确，三点到平面距离相等就可以得到直线上的每一点到平面的距离都相等.

师：这个判定方法在实际操作中方便吗？

生：需要测量三个点的距离，不好操作.

师：在空间中，作出点到面的距离并不是件容易的事，因此这个判定方法需要进一步改进.大家回忆一下，在初中我们是如何判断线线平行的？

生8：利用角度关系，比如内错角相等、同旁内角互补等.

生9：利用平行四边形的性质，平行四边形对边平行.

师：这说明判断平行的思路有很多，可以借助角的关系，也可以借助线的关系.那么，刚才我们是利用“距离关系”判定线面平行，能否换一个几何关系？

生10：可以利用线线平行来判定线面平行.我发现日光灯与它在地面上的影子是平行的，从中可以得到如果能够在平面内找到一条直线与平面外的直线平行，那么这条直线就与平面平行.

师：观察的很细致，大家认为这个结论正确吗？

生：正确.

师：为什么？

生11：如果平面外一条直线平行与平面内的一条直线平行，那么这条直线上的每一点到平面的距离都相等，这和我们借助“距离”的判定方法是等价的.

随着立体几何学习的深入，学生会获得越来越多的“经验”.有三大经验贯穿立体几何学习的全过程，一是“降维的经验”，将空间问题平面化，把立体几何问题转化为平面几何问题；二是“化无限为有限的经验”，在判断线面空间位置关系中，往往把“任意一条直线”转化为“两条相交直线”；三是“引进第三个几何元素作为中介来刻画两个几何对象的关系的经验”，比如，利用线线平行来刻画线面平行、借助线面垂直来刻画面面垂直等.因此，联系已有的经验，通过“思辨”，有助于更快地明确几何论证的方向.

三、构造模型对比，“思辨”结论的完备性

立体几何模型是对立体几何知识的集中概括，是凝结在学生头脑中的一系列的加工和认识对象，学习立体几何就是学习各种各样的几何模型“打交道”.在立体几何教学中借助模型进行“思辨”不仅能够使学生直观地发现蕴藏在图形内部的定理与性质，而且有助于学生精准地用数学语言把这些定理与性质表述出来.

师：通过对原先方法的改进，我们得到判定线面平行，只需要判定线线平行.在生活中有这样的例子吗？

生12：开门、关门时，门框线始终与墙面平行，因为门框线与门轴平行，而门轴在墙面上.

生13：翻开书本中的某一页时，这页的边始终与书本保持平行，它的原理与开门、关门类似.

师：那么这个判定方法一定正确吗？

生：感觉是正确的，但无法证明.

师：我们可以借助模型加以理解，如图1所示，两平行线AC、BD分别交平面α于A、B两点，可以把这两条平行线想象成“滑竿”，现将平面α内的直线AB顺着这两根“滑竿”滑到平面α外MN处，如果MN始终与AB保持平行，那么MN与平面α平行吗？

意图：借助“滑竿”模型进行“思辨”有助于学生把平面外的直线与平面内的直线联系起来，有利于学生在后续的学习中更好地掌握和运用“线面平行”的判定定理.

生：一定平行.

师：我们可以这样理解，平面α可以看成由直线AB平移中形成的轨迹，也就是说无数条与AB平行的直线构成了平面α，如果MN与AB平行，那么MN就与平面α内无数条直线平行，且不会有交点，那么直线MN就一定与平面α平行.

师：如果MN不与AB平行，那么直线MN会与平面α平行吗？

生14：不平行，如果MN不与AB平行，则MN一定与AB相交，那么MN就会与平面α有交点

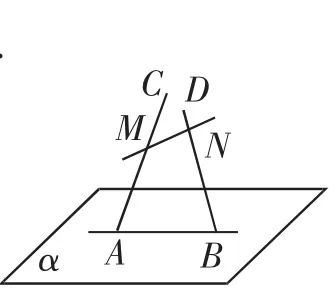
图2

师：我们再换个模型，若直线AC、BD是两条异面直线（如图2），其余条件不变，则直线MN与直线AB还有可能平行吗？直线MN与平面α还有可能平行吗？为什么？

意图：对线面平行判定进行更为深入的“思辨”：平面外的直线与平面内的某一条直线不平行，并不代表它和平面内的其余直线都不平行，因此不能判定直线与平面一定不平行，平面内符合定理要求的直线“存在”即可，这也是应用定理的关键

生15：直线MN与AB不平行，如果平行的话，MN与AB就共面，即直线AC、BD共面，这就与题目条件矛盾.

生16：MN可以与平面α平行，只要能够在平面α内找到一条直线与MN平行就可以了.

师：经过上述分析，你能准确描述线面平行的判定定理吗？

……

四、拓展应用，“思辨”解题的套路

图1

“线面平行的判定”可以说是立体几何的“起始课”，因为，从这一课开始学生正式经历用几何论证的方法研究空间中点、线、面之间的位置关系.掌握线面平行的判定方法只是其中一方面，更为重要的是通过这节内容的学习，使学生了解研究空间中几何对象之间位置关系的一般“套路”，而这种套路的掌握对于后续面面平行、线面垂直、面面垂直的判定具有重要的借鉴意义.因此，以典型例题为载体，探究判定定理的应用技巧，引导学生“思辨”解题的套路，促进学生的几何论证思维趋向严密.

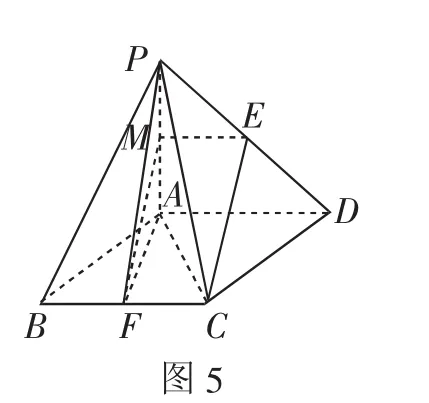
题目如图3，在四棱锥P-ABCD中，底面ABCD是平行四边形，E、F分别为线段PD和BC的中点，求证：CE∥平面PAF.

意图：通过探究，对线面平行问题的解题套路进行深入的“思辨”.首先是考虑怎么证明线面平行？接下去考虑判定定理怎么用？需要什么条件？最后考虑有几种不同的实现路径.

线面平行的判定，关键是在平面内找到与已知直线平行的直线.一般有两种方法：一是利用中位线的性质找平行线；二是构造平行四边形找平行线.这两种方法对于本题都适用，分别如图4、5所示.

图3

对本题的解题方法的“思辨”最终使学生掌握解决线面平行证明的一般套路，如图6所示.

图6

“思辨”本质上是对问题的一种理性的思考，数学学习离不开“思辨”.空间中的几何位置关系错综复杂，通过“思辨”拨开重重“迷雾”找到问题的真相，从而促进思维趋向严密，实现深度学习.