利用数学直观解决问题的几点思考与案例研究

☉江苏省宜兴市和桥高级中学 杜 健 张 菁

一、引言

很多学生往往在讲过多次、练过多次的题目上还会失分，细细想来，这应该是学生对诸多解题之法并没有真正理解与掌握的缘故，思及至此.笔者不禁对自己的解题教学进行了回忆与审视，对一些过于形式化、解析化的解法进行了新的思考.本文结合实际例题对追求形式化的技巧到寻求直观上的解法这一理解加深的过程进行了新的审视.

二、样例

集中体现教材与学生认知水平之间矛盾与冲突的范例更加容易引起学生的认知冲突，使学生在浓厚的兴趣中获得关于事物关系的经验并认识到更加抽象或概括性的规律.

问题1A，B两地是铁路线上相距100km的一个路段，工厂C与A处相距20km，AC⊥AB，为了节约运输过程中的时间，现在AB线上选定一点D并从D处修出一条直通工厂的公路，铁路上货运与公路上货运的运费之比是3∶5，从B处运货到工厂C点运费最少的话应将D点选在何处？

评析：设AD=xkm，则设铁路货运费用为3k/km，公路货运费用为5k/km，则运费为其中0≤x≤100，然后对函数求导数并取极值求得函数的驻点，即为D点的位置.这是比较常见的，另外还能引入三角变换，设x=20tanθ，由0≤20tanθ≤100，得出则300，处理需用这一“二合一公式”，不过学生对这一公式的运用往往不很熟练，学生对这一解法所隐含的意义也不能很好了解.因此，教师可以引领学生对一些富含深刻意义的直观解法进行探寻和理解.

解法1（折算法）：如图1，E是C关于AB的对称点，铁路货运与公路货运之比是3∶5，因此可以理解成铁路货运5km的费用花在公路货运上只能走3km，则铁路DB段费用折算成陆地DF上费用有总费用则为y=5k·CD+3k·DB=5k（CD+DF），求出点C到直线BE的距离即为费用的最小值.此时C、D、F三点共线且CD⊥BE，则有

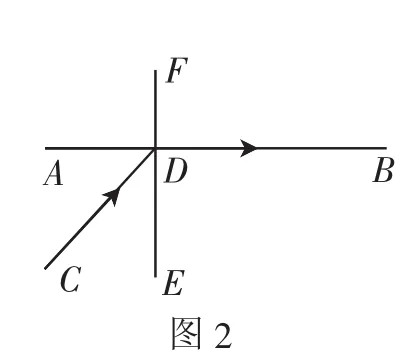
解法2（物理解法）：光线在光学介质中从A点至B点所走的实际路程是连接A，B两点的所有曲线中最短的，光线自动选择光程最短路径进行传播的光行最速原理也可以用于本题的解决.将陆路上、铁路上的运输与光行最速原理结合起来思考，借助c=vn（c代表光在真空中的光速，v代表光在折射率是n的介质中的传播速度）这一公式，将“费用”看成为速度，则“一定的费用”即可看成为光速，则铁路每公里的费用3k与公路每公里的费用5k即相当于光在其中的速度分别为3k和5k，从公路到铁路的运输也就相当于光线从某一介质到另一介质所发生的全折射.

高中数学教学很多时候需要这一直观解决问题的方法起到一定的支撑与指导作用，2003年的全国高考数学理科卷以及2007年的湖南高考数学理科卷就重复出现类似的问题，对当时的考生都造成了较大的困扰.

不过，我们从上述两种直观解法上也不难看到数学形式化技巧背后所隐藏的丰富含义.数学形式化、符号化之后的丰富含义一旦得到揭示，数学理论与其他自然学科之间的有机联系便能够更好地展露出来，数学理论的普适性与有机统一才能在更有意义的范畴内获得统一.

问题2已知圆盘x2+y2≤a2，求其绕x=-b（b＞a＞0）旋转所成旋转体的体积是多少？

评析：此题的形式化解法共有两种，一是将两个旋转体的体积看成为这两条曲线绕x=-b所旋转成的几何体的差，即另一解法是将该几何体看成为“面”旋转而成的，根据对称性可考虑圆的上半部，则该旋转体的上半部即可看成为很多形如图3中DEGF的“面”旋转积累而成的几何体.假设点E的横坐标是x，EG=dx，则体积微元近似于

这是微积分在几何中的应用，那么此题的解决可有直观化的解法吗？

解：x2+y2≤a2的圆盘面绕直线x=-b旋转一周形成了一个几何体，其环圆心O绕直线x=-b旋转则形成了一个周长为2πb的圆周.采取一定方式将环切开能够得到一个直圆柱体，其底面积是πa2，高是2πb，则该直圆柱体的体积为πa·2（2πb），即该环的体积为2π2a2b.

这是一个开普勒在微积分发展之初就思考过的问题，开普勒的想法是运用无数同维无限小元素的和对曲边形面积、旋转体体积进行确定，不仅如此，开普勒将球的体积也看成为无数顶点在球心的小圆锥的体积之和，球面的一部分可以看成是底面积，则球的体积能够看到形式背后的直观才意味着解题者掌握这一知识已经达到熟练化、深度理解的层面.

问题3若ξ～B（n，p），则Dξ=npq，q=1-p.

评析：二项分布方差的推导在一般的概率统计教材中都有呈现，有的推导过程相对来说稍微复杂一些，以下推导法是一种比较简单的方法.在两边同时对x求导，有两边同乘以x可得对上式中的x同时进行求导，有令x=p，有Eξ2-（Eξ）2=npq.这一推导法在计算上的量显然更小一点，不过，大多学生并不容易想到这一方法，但很多复杂事件都可以理解成众多系列性的基础事件的组合，因此，在具体的解题操作中完全可以将简单事件的性质联系起来并以此为基础来把握复杂事件所具备的性质，以简驭繁的解题目的也就更加容易达成了.

解：假如随机变量ξ～B（n，p），因此可以将ξ看成n重贝努里试验中事件A所出现的次数，将A每次在试验中出现的概率假设为p，则可以令在第i次试验中A出现的次数ξi为1，令在第i次试验中A不出现的次数ξ1为0，则ξ1（1≤i≤n）为服从0-1分布的随机变量，所以另一方面则

这一分解合成法和力的分解合成相比显现出了异曲同工的巧妙之处，事件的分解合成、线性微分方程解的构造、数论中孙子定理的推导、某些不等式的证明、拉格朗日插值公式等内容都可以运用这一方法.

三、结束语

数学家怀特尼曾经提倡大家对工作的研究应尽量自然，我们在具体问题的解决中也应该力求自然和直观.背景、图像等给人的感觉相对都更加直观，值得注意的是，“图像”并不一定就是我们通常联想的具体画面，很多概念的心理成像能力也包含在“图像”的范畴之中，此处所说的心理成像能力即为解题者将某一事物想像成为其他事物或其他样子的能力.事物复杂性的图形得到具体有效的展露，学生对于具体事物所包含的概念才能形成充分的理解.由此可见，从某种意义来讲，对所要学习或研究的事物的思考想象能力也是“图像”的一种具体体现.概念与事实在这一方式的展露中变得不再是外在于人的存在，学生通过心理成像便能够更好地发挥出数学思考与想象的创造力.“真实的概念意味着能够呈现客观事物复杂性的图像”，这一维果茨基的名言对于我们高中数学的教学实践来说存在着相当深远的含义，我们在实际教学中应不断研究复杂问题的直观化解法以帮助学生在化简驭繁的解题中真正理解知识.