纳米尺度孔边裂纹裂尖Ⅲ型应力强度因子研究
2018-10-22肖俊华崔友强徐耀玲张福成
肖俊华 崔友强 徐耀玲 张福成
1.燕山大学河北省重型装备与大型结构力学可靠性重点实验室,秦皇岛,066004
2.燕山大学亚稳材料制备技术与科学国家重点实验室,秦皇岛,066004
0 引言
机械零部件上常常含有孔洞,如螺栓孔、铆钉孔、键槽和减重孔等[1-2],在冲击载荷和高频率振动等复杂服役条件下,孔边应力集中现象非常明显,极易形成微裂纹[3-4]。在外载荷作用下,孔和裂纹相互作用,会显著影响结构的强度性能[5]。
国内外针对孔边裂纹问题强度性能的研究,从研究方法来看有细观力学理论分析、试验测试和数值模拟等,其研究成果在机械制造、航空航天结构、压力容器和土木工程等工程结构和材料的强度设计、安全可靠性分析和缺陷评定规范中得到广泛应用。
当孔边裂纹的尺寸在纳米尺度时,孔边应力场分布和裂尖应力强度因子受其表面效应影响显著。对于纳米尺度裂纹问题,高克玮等[6]基于原位拉伸观察研究了纳米级解理微裂纹的形核和扩展行为;利用分子动力学方法,MACHOVÁ等[7]研究了含纳米尺度裂纹时体心立方铁的韧性和脆性特征;邢永明等[8]应用纳米云纹法测量单晶硅微裂纹尖端变形,得到了准解理微裂纹裂尖的纳观应变场;邵宇飞等[9]通过准连续介质方法模拟了纳米多晶体Ni中裂纹的扩展过程;LE等[10]基于概率理论研究了准脆性和脆性结构的强度、静态裂纹萌生、寿命及尺度效应;JONES等[11]提出了纳米复合材料内疲劳裂纹萌生的机理模型和预测表达式;LI等[12]基于晶粒旋转和晶界剪切耦合迁移方法探究了耦合裂纹的钝化机理;LUO等[13]研究了考虑界面应力时偏转纳米线的应力场和裂纹成核行为;GAO等[14]利用相位晶体法研究了纳米尺度裂纹扩展过程。
在表征纳米尺度微结构的诸多理论中,Gurtin-Murdoch表面弹性理论[15]通过引入表面应力,将连续介质力学中的宏观特征尺寸与纳米缺陷的特征尺寸跨尺度响应进行了统一描述,该理论及其推广理论被广泛应用于纳米非均匀材料力学性能研究中。基于Gurtin-Murdoch模型和格林函数法,WANG等[16]讨论了表面性能对各向异性双材料界面裂纹的影响。NGUYEN等[17]利用有限元和伽辽金边界元耦合方法研究了三维线性弹性介质中I型片状裂纹的尺寸依赖行为。XU等[18]分析了反平面载荷作用下纳米夹杂和纳米裂纹应力场的相互干涉。WANG等[19]讨论了具有表面弹性性能时Ⅲ型桥接裂纹的断裂性能。WANG等[20]进一步研究了考虑表面效应时Ⅲ型速率依赖性桥接裂纹的桥接力和裂纹张开位移等问题。
本文基于Gurtin-Murdoch表面弹性理论[15]和保角映射技术,利用复变弹性理论,研究纳米尺度下圆孔孔边裂纹的反平面剪切问题,获得了该类非均匀材料应力场的解析解,给出了裂尖Ⅲ型应力强度因子的闭合解,分析了孔边应力场分布规律,讨论了裂尖应力强度因子的尺寸依赖效应以及圆孔相对尺寸对应力强度因子的影响规律。
1 纳米尺度孔边裂纹模型和基本方程
图1为纳米尺度圆孔孔边裂纹示意图,远场受均匀反平面剪切载荷。以圆心为坐标原点,圆孔半径为R,圆孔区域用Ωc表示,边界用S表示,基体区域用Ωm表示,基体剪切模量为Gm,裂纹CD长度为L。下标c、m分别表示圆孔和基体。
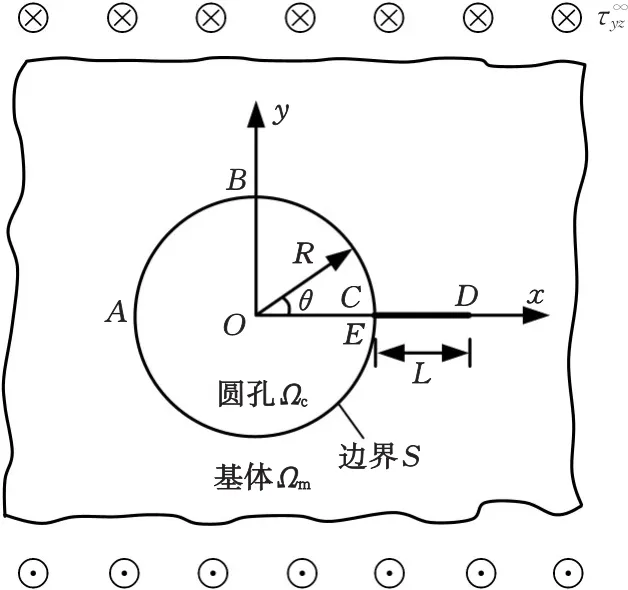
图1 纳米尺度圆孔-孔边裂纹反平面剪切问题示意图(z平面,z=x+iy)Fig.1 Schematic diagram of nano crack emanating from a circular hole under antiplane shear(z-plane,z=x+iy)
用w=w(x,y)表示纵向位移,基体内的平衡方程和本构方程满足:

由复变弹性理论可知,在复平面内纵向位移w、应力分量τxz和τyz可用一个解析函数Ψ(z)(z=x+iy)来表示:
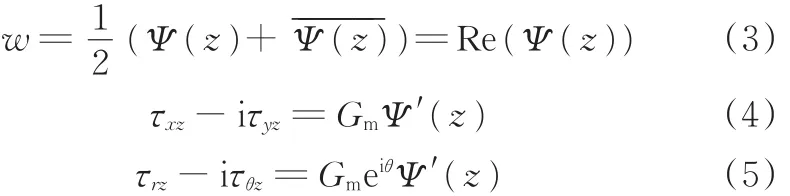
式中,τrz、τθz分别为柱坐标系中两个切应力分量。
纳米尺度圆孔边界上的位移和应力边界条件为[21]
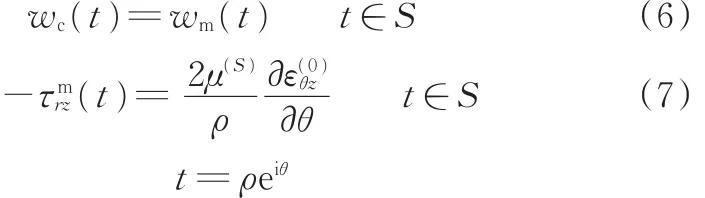
式中,μ(S)为表面弹性常数;(ρ,θ)为纳米尺度圆孔边界上点的极坐标为界面应变分量。
2 问题转换与应力场解答
将图1所示含孔边裂纹圆孔外部分保角变换为图2所示半径为R的圆外部分,变换函数[22-23]
如下:


图2 保角映射(ζ平面)Fig.2 Conformal mapping

将解析函数Ψ(z)在ζ平面内展开成Laurent级数形式[24]
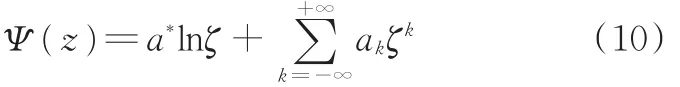
式中,a*、ak为待定常数。
由分析可知采取下述有限项级数形式就可以得到问题的解:式
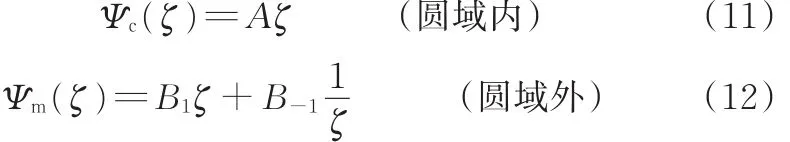
中,A、B1和B-1为复常数。
利用远场条件,由式(4)和式(12)可得

由界面条件式(6)和式(7)可得
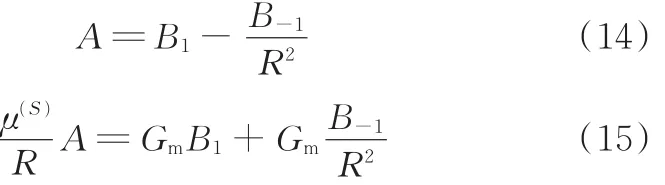
联立式(13)~式(15)可得

由式(4)、式(11)~式(13)、式(16)和式(17)得到基体内的应力场表达式为
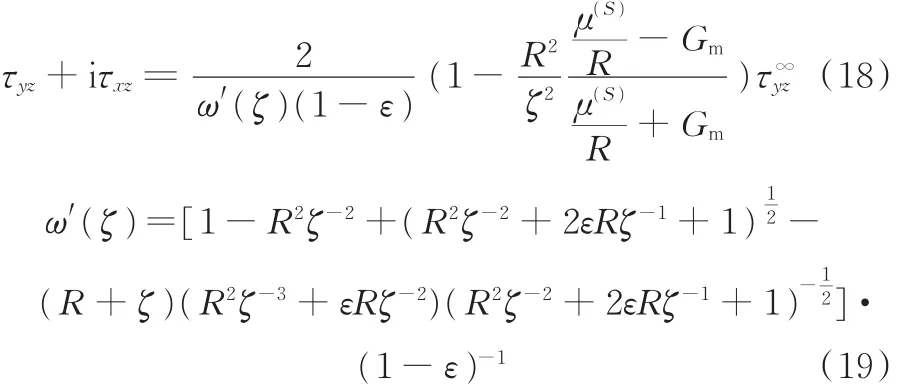
3 裂纹尖端Ⅲ型应力强度因子
在图1所示z平面内定义裂尖处应力强度因子如下:
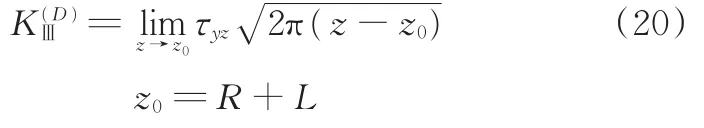
将式(18)代入式(20),在ζ平面内,可得

注意到裂尖处ω′(R)=0,对式(21)利用洛必达法则,可得式中,L′为等效裂纹长度。

故K(D)*为裂纹尖端等效量纲一应力强度因子,
若不考虑表面效应,即μ(S)=0时,式(23)退化为

式(24)与文献[22]中纯弹性变形情形结果一致。
4 算例与讨论
4.1 孔边应力场分布
表面弹性常数μ(S)的量级为1 N/m,可以通过原子模拟得到,其数值可正可负。定义参数α=μ(S)/Gm,α的取值范围一般在(-2~2)×10-10m之间[21]。
图3给出了孔边不同位置下应力集中系数的分布情况,取R=3 nm,L=R,可知,当孔边位置角θ从0o变化到180o时,孔边应力从零开始先增大然后减小最后再增大。当θ约为30o和90o的位置时应力分别取极大值和极小值,在θ为180°位置时应力取最大值。θ从0°变化到90°过程中,纳米圆孔的表面效应(α取值对应力的影响)逐渐显著;θ从90°变化到180°过程中,表面效应先减弱而后增强。上述结果表明:表面效应对孔边不同位置应力的影响程度不同。
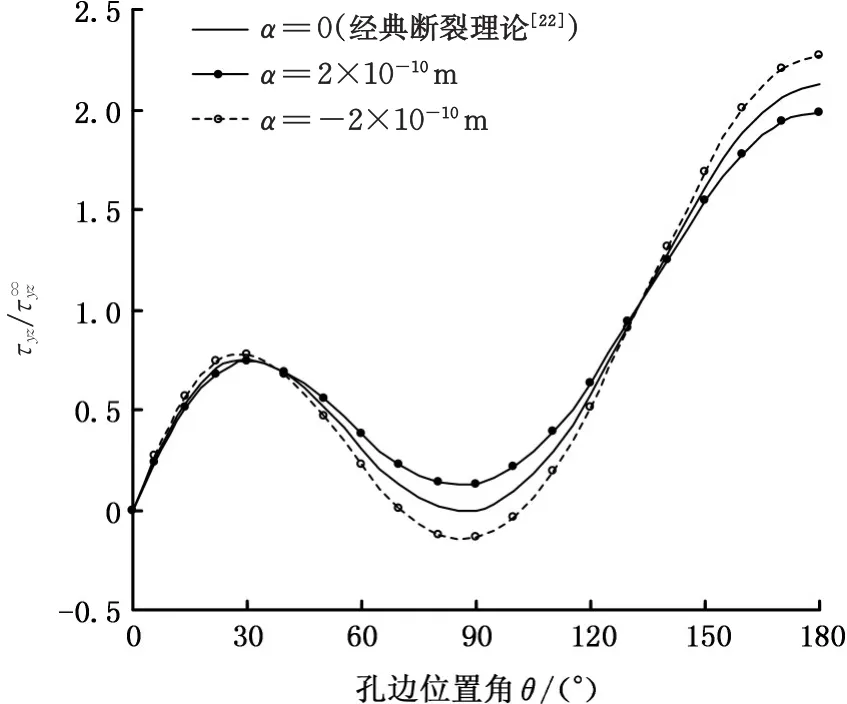
图3 孔边应力集中系数分布Fig.3 Distribution of the stress concentration factor at the hole
4.2 应力强度因子的尺寸依赖效应
图4 给出了裂尖量纲一应力强度因子K(D)*随圆孔裂纹尺寸的变化趋势,其中L=R。

图4 圆孔裂纹尺寸对裂尖量纲一应力强度因子的影响Fig.4 Influence of size of the hole-rack on the dimensional stress intensity factor at crack tip
由图4可以看出,不考虑表面效应时(α=0,经典断裂理论),应力强度因子与圆孔裂纹的尺寸无关;考虑表面效应(α≠0)且圆孔裂纹的尺寸在纳米量级时,应力强度因子具有显著的尺寸依赖效应。随着圆孔裂纹尺寸的增大,表面效应的影响逐渐减弱,本文结果趋近于经典断裂理论解。
4.3 圆孔相对尺寸对应力强度因子的影响
圆孔相对于裂纹尺寸比值R/L对应力强度因子的影响曲线见图5,其中L=5 nm。图中显示一个有趣的现象,即:圆孔相对尺寸对应力强度因子的影响规律受表面效应α取值的制约。随着比值R/L的增大,当不考虑表面效应时(α=0),量纲一应力强度因子从1开始先略微增大随后减小;当α取正值时,量纲一应力强度因子先增大而后减小;当α取负值时,量纲一应力强度因子单调减小。
图5还显示,当圆孔相对尺寸较小时(R/L<1),改变α显著影响应力强度因子;当圆孔相对尺寸较大时(R/L>1),不论α取值如何,应力强度因子趋于相同值。这表明,表面性能对应力强度因子的影响也取决于圆孔相对尺寸R/L,非常大的圆孔相对尺寸屏蔽了表面性能对应力强度因子的影响。

图5 圆孔相对尺寸对应力强度因子的影响Fig.5 Influence of relative size of the hole on the dimensional stress intensity factor
5 结论
(1)当圆孔裂纹的尺寸在纳米尺度时,裂尖应力强度因子具有显著的尺寸依赖效应;随着圆孔裂纹尺寸的增大,纳米尺度圆孔的表面效应逐渐减弱,本文结果趋于经典断裂理论解。
(2)圆孔表面弹性常数μ(S)不同时,裂尖应力强度因子随圆孔相对裂纹尺寸R/L的变化规律迥异:随着比值R/L的增大,不考虑表面效应时(α=0)量纲一应力强度因子从1开始先略微增大随后减小,当α取正值时量纲一应力强度因子先增大而后减小,当α取负值时量纲一应力强度因子单调减小。同时表面性能对应力强度因子的影响也取决于圆孔相对尺寸:当圆孔相对尺寸较小时(R/L<1),改变表面性能显著影响应力强度因子,当圆孔相对尺寸较大时(R/L>1),不论表面性能如何,应力强度因子趋于相同值,非常大的圆孔相对尺寸屏蔽了表面性能对应力强度因子的影响。
