酸洗连轧生产线机组轧制功率建模及工艺参数优化

杨 杰 宋 健 胡 琦 张超勇 孟磊磊

1.中国地质大学（武汉）机械与电子信息学院，武汉，430074

2.华中科技大学数字制造装备与技术国家重点实验室，武汉，430074

0 引言

我国冷轧生产所用的设备主要是各类大型机器装备，其额定功率远远大于普通机床装备的额定功率，大部分设备的额定功率是通用数控机床额定功率的十几倍到几百倍不等。受当前市场因素影响，企业更加关注交货期和产品质量，忽视高能耗下能源利用率低的问题，且对冷轧工艺能效提升技术的研究较少。本文引入能量流方法分析冷轧生产线中酸轧工艺的能耗评估，研究能耗与工艺参数之间的关系。

目前，关于冷轧节能降耗的研究非常少，江东海等［1］对六辊单机架冷轧节能降耗技术进行了探讨，对减少电耗、辊耗、油耗的措施进行了讨论。其他研究中，有的针对非冷轧工艺，如LU等［2］提出了热连轧加热炉的能量分配模型，获得了带钢在不同加热炉的能量消耗规律；有的针对设备的改进，如KARANDAEVA等［3］提出利用节能晶闸管进行轧机驱动。

能量流作为一种评估制造业能效的工具，较早出现在数控机床系统能耗研究中，并且在该领域的研究已比较成熟。王秋莲等［4］针对数控机床多能量源的特性，从能量源构成出发对其能量流的数学模型进行了研究。酸洗连轧生产线同机床系统类似，是一个复杂的多机电系统，故能量流的方法可以借鉴用在酸洗连轧生产线的能耗研究上。

本文利用能量流的理论方法，针对酸洗连轧生产线，建立电功率能量流模型，获得轧制能耗能量输出与工艺参数之间的关系，用于描述酸洗连轧生产线的能量消耗情况，以及指导后续的能量优化研究。

加工过程中合理调节工艺参数可节约能量和资源，提高能量效率。目前已有与酸洗连轧轧制工艺相关的工艺参数优化研究，但研究存在以下两点不足：一是单参数优化，只考虑压下量的优化问题而忽略其他工艺参数对功率的影响；二是能耗模型过于简单，无法用常规的数学方法进行求解。对于非线性优化问题，本文采用一种改进的粒子群算法，对五机架连轧机的功率模型中的参数进行优化。

1 基于能量流的机组功率模型

本研究针对酸洗连轧生产线（简称“酸轧产线”）建立轧制能量流模型。五机架连轧机是酸轧产线的核心机组，用于将热轧坯料轧制成符合要求厚度和宽度的薄板，轧制工艺能耗占酸轧产线能耗的主要部分。以五机架连轧机组为研究对象，利用直接建模法建立机组轧制输出能量与参数之间的平衡方程。模型相关参数如下：轧制工艺所需功率Pz、上下两轧辊共同作用的轧制力矩Tz、轧辊转速ni、电机传动到轧机的传动效率η、轧制压力p、轧制力臂长度α、平均单位压力pˉ、力臂系数ψ（与轧制工艺有关）、轧件平均宽度bˉ、不考虑弹性压扁时的接触弧长度l、考虑弹性压扁时的接触弧长度l′、与工艺有关的系数m、轧制时的前后平均张力qˉ、轧件的变形抗力k、轧辊与带钢之间的摩擦因数f、轧件轧制前后的平均厚度hˉ。

1.1 轧制工艺功率模型建立

酸轧产线机组众多，本文只选取电机功率最大（5 250 kW）的轧机机架进行建模分析，其余机组建模方法与单个轧机机架的建模方法类似。

轧机将厚度为1.5～6.0 mm的热轧钢板原料轧制成厚度为0.2～2.0 mm的薄板，其轧制工艺可简化为考虑弹性压扁的带钢弹塑性形变模型［5-7］，见图1。轧制的能耗即在生产过程中的工艺能耗，轧制工艺所需功率

图1 考虑弹性压扁的弹塑性变形模型Fig.1 Elastic plastic deformation model concerned elastic flattening

得出轧制所用力矩

故

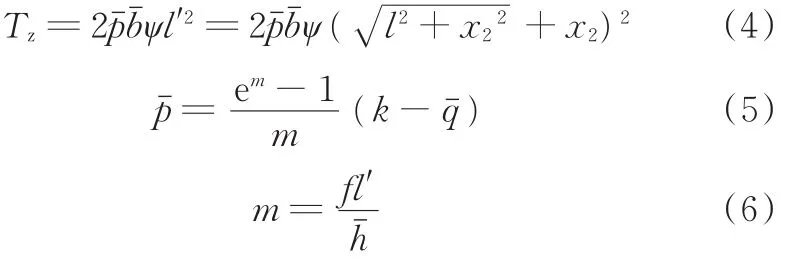
公式中，轧件的变形抗力k采用周纪华-管克智的变形抗力计算模型［8］。

由于l′待定，故上述方程中pˉ也无法确定。通过式（5）和式（6）迭代求得l′，迭代过程见图2。

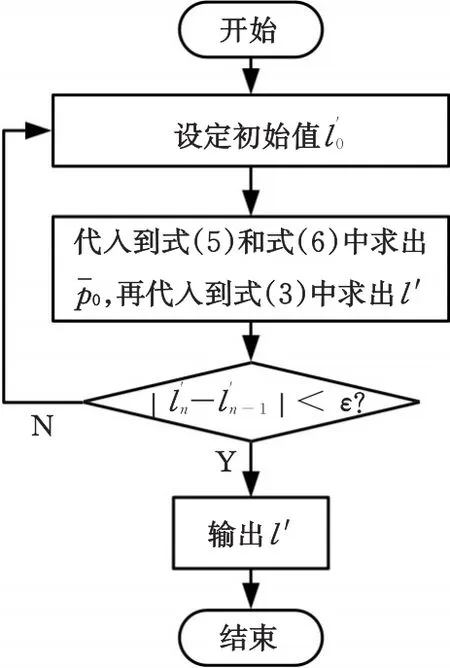
图2 迭代法示意图Fig.2 Iteration diagram

根据金属秒流量相等的原则计算轧辊转速ni，即单位时间通过的带钢体积相等。第一机架的轧制速度可根据工艺要求获得，则带钢的运行速度vi可由下式求得：

那么轧辊的转速可由下式求得：

图3中，1～5表示1号到5号轧机，6表示卷取机，根据单个机架轧机的功率模型，可以得到带钢厚度、压下量、钢种的弹性模量等参数与轧制功率的函数关系。根据钢卷轧制的要求以及钢卷的机械性能，轧制过程中轧机所需功率

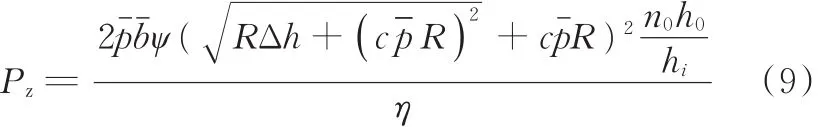
式中，R为轧机机架的工作辊的半径；Δh为压下量；c为中间系数。

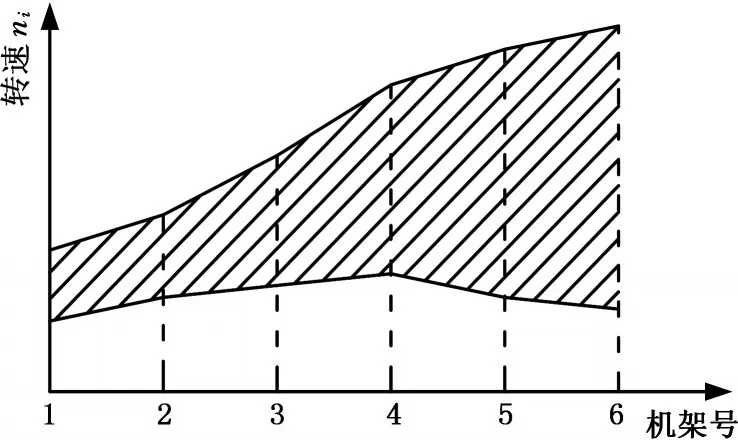
图3 五机架连轧机速度锥Fig.3 Speed cone of five stand with rolling mill

1.2 轧制工艺功率模型的校核

酸洗连轧属于流程式生产，具有连续性的特点，一旦启动将不能随意停机，受目前技术限制，轧机的实时功率无法通过实验方法直接获取。本文通过代入实际参数计算轧机所需的某一最大功率，然后与轧机容量进行比较，来校核模型的可靠度。本文的功率模型是基于某冷轧厂的酸洗连轧产线建立的，涉及的机组参数数据由该冷轧厂提供。校核用钢种的参数以SUS304钢种为例，与工艺有关的参数通过文献［9］获取。功率模型中出现的机组工艺参数见表1。

表1 模型中参数值Tab.1 Value of parameters in model

最大压下量

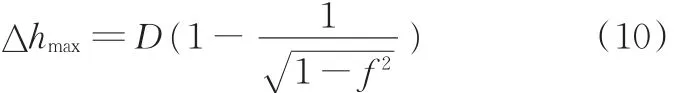
假设在1号机架进行轧制，采用式（10）计算最大压下量，并假设样本的宽度与工作辊长度相等，力臂系数取0.4，将表1中数据代入式（9），可得

最终得出轧制SUS304钢种对应的轧机所需功率为4 029 kW。表1中1号机架的电机容量M=4 174 kW。

模型计算数据的绝对误差

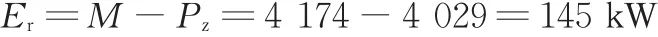
模型计算数据的相对误差

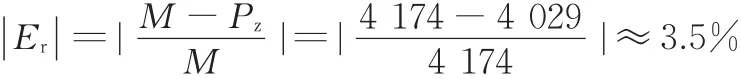
模型计算得出的结果显示，模型仍有一定的误差，绝对误差为145 kW，相对误差为3.5%。如果数据来自其他钢种，则变形抗力有所不同，计算结果也会不同，因此模型具有一定的可靠性，但仍有待进一步改进。

2 基于功率模型的工艺参数优化

轧制功率Pz是一个关于压下量∆h、前后平均张力qˉ、轧制转速ni的一个高次非线性的方程。要减小轧制所需功率，需要获得最优参数，同时设定三个参数在合理的值域内，因此轧制工艺参数优化可以看成是一个多维度的寻优问题。

2.1 板型优化问题描述

在优化工艺参数使能耗最低的同时，还需考虑板形质量问题。板形的缺陷主要来自于应力作用，尤其是带钢内部存在的内应力，当它大到一定程度后，会使带钢产生明显的板形缺陷，通常表现为中浪或者边浪。

造成带钢板形缺陷的外在因素主要是轧制力，当轧制力过大时会造成轧辊发生挠曲变形，使得施加在带钢上的力分布不均匀，无法满足带钢板形良好的要求。板形良好的基础是保证轧制前后断面形状一样，见图4，He是轧制之前边缘厚度，he是轧制之前中部厚度,H(x)是带钢轧前沿宽度的厚度，h(x)是带钢轧后沿宽度的各处厚度，假设轧前带钢的长度为L(x)，轧后长度为l(x)，则有

图4 带钢轧制断面图Fig.4 Cross-section diagram of strip steel when rolling

由上述条件推出常用保证板形良好的条件如下：

式中，CH、Ch分别为轧制前和轧制后的带钢凸度；Hv、hv分别为轧制前后带钢的平均厚度。

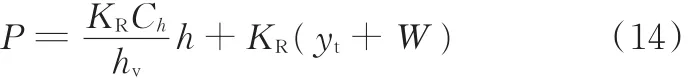
式中，KR为轧辊刚度系数；yt为工作辊的热凸度值；W为原始辊形凸度值。

为保证板形良好的要求，轧制力P必须满足：

式（14）在图5中表示阴影区域的中线，粗轧时对板形的要求不是太高，落在阴影区即可。

图5 轧制力对板形的影像图Fig.5 Influence of rolling force on shape of plate

2.2 优化函数模型设定

根据式（9）的计算过程可以得出，在轧机工作过程中，与轧机功率有关的参数主要为压下量、轧制速度和平均张力，这三个参数也是主要的优化参数。为保证板形良好，即轧制前后凸度相同，需要保证轧制力在一定范围内。

约束条件主要有：①产品质量；②生产时间和生产效率；③机组能力。超出合理范围的工艺参数会影响机组的使用寿命，导致机组提前损坏。

函数模型如下：

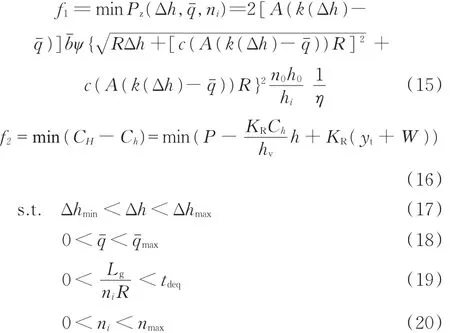
式中，Lg为某一带钢的长度；tdeq为设定的最大加工时间；nmax为轧辊要求最大转速；A代替式（5）中的其他参数。

式（15）为能耗优化函数，其中∆h、qˉ、ni为优化参数，k是以∆h为变量的函数。式（16）为板形优化函数，即保证在轧制力取值范围内轧辊不产生较大挠度。式（17）为压下量约束，基于对轧机的保护，以及对轧制产品的质量保证，轧制规程规定每一轧制道次的压下量不能超过某一数值，其中∆hmax由咬入条件确定，最小压下量∆hmin用来防止轧制后带钢晶粒粗大。式（19）、式（20）为最长轧制时间及最大轧制速度约束，当轧制速度减小时，轧制时间随之延长，若轧制时间过长，则无法保证某些订单的交货期，因此轧制速度不能小于某一值，同时由于轧机能力有限，轧制速度也不能过大。

该优化问题为含有2个优化目标和4个约束条件的多目标优化问题。本文采用约束法对工艺参数进行多目标优化，将板形优化目标转化为约束条件。

2.3 采用的算法及主要步骤

现有轧制工艺参数优化算法有动态规划算法、极限差值法，这些方法在考虑机架间压下量分配问题时比较适用，但在单个机架上求解高次非线性问题时却并不适用［10］。

针对冷轧轧制优化问题的高次非线性以及实际生产数据量大的特点，本文采用一种改进的粒子群算法对单个轧机机架的工艺参数进行优化。在原有基础上，引入一种非线性权重递减策略［11］，以解决粒子群算法容易陷入局部最优解的问题。该策略使得搜索初期的惯性权重值ω尽可能地大，使得设定群的粒子能够飞跃整个搜索空间，以得到较好的多样性，避免过早陷入局部极值；当算法搜索到种群的全局极值附近时，应该及时快速地减小惯性权重值ω，并且在搜索后期保持比较小的ω，使得该种群以较强的局部搜索能力收敛到全局极值。基于三角函数特征动态调整惯性权重ω，其变化公式为

式中，a为递减系数；g为迭代次数；gmax为最大迭代次数。

采用约束函数判断法来实现对目标函数的约束，个体译码后，计算相应的各参数值并代入约束函数。如果不等式不成立，则令该个体适应值为0；否则继续计算下一约束，直到所有约束被满足，再计算个体的目标函数值。

算法实现的基本流程如下：

（1）基本参数设置。主要有最大迭代次数gmax、最大加工时间tdeq、最大轧制速度nmax、最大平均张力qˉmax、最大以及最小压下量Δhmax和Δhmin。

（2）依照粒子群的初始化过程对粒子群的初始位置和初始速度进行随机初始化。本文的优化模型含有多个变量，因此属于多维优化问题，初始化内容如下：

式中，p0为粒子每个参数的初始位置；v0为粒子每个参数的初始速度。

（3）计算适应度。由于本文的优化问题为最小化问题，因此适应度函数为待求解函数乘以-1。

（4）遍历所有粒子。若每个个体的适应度Fj(x)比其最佳位置pbest(j)大，则pbest(j)=Fj(x)，将每个粒子的最佳位置pbest(j)与全局最佳位置gbest(g)进行对比，当pbest(j)＞gbest(g)时，gbest(g)=pbest(j)，并判断是否满足约束。

（5）根据以下公式更新个体的速度与位置：

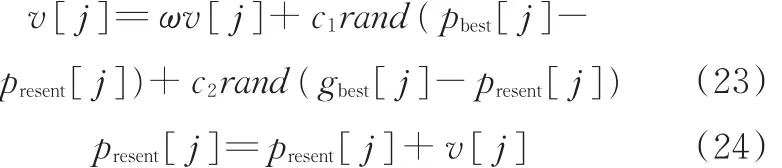
式中，c1、c2为学习参数；present[j]为第j个粒子的当前位置。

（6）重复步骤（3）～步骤（5），达到最大迭代次数gmax时，终止算法，并输出最优值。

3 结果分析

本文引入了非线性递减策略，经过多次尝试，当式（21）中系数a=0.05时，优化效果最好，惯性权重ω变化曲线见图6。

图6 惯性权值非线性递减图（a=0.05）Fig.6 Nonlineary decrease of inertia weight（a=0.05）

其他工艺参数取值见表1。同样以SUS304钢为例，出口厚度为1.0 mm，宽度为1 175 mm，设初始速度为9 m/s，初始张力为90 MPa（9 000 000 kgf/m2），初始压下量为最大压下量。假设在1号机架进行轧制。根据式（21），利用MATLAB语言对算法进行编程，优化结果见表2。

由表2可以看出，压下量为0.15 mm时轧制功率最低，而轧制速度的值越小越有利于轧制功率的降低，平均张力越大也越有利于轧制功率的降低。

表2 工艺参数优化结果Tab.2 Result of Process parameter optimization

为便于直观分析表2中优化结果，利用MATLAB得到能量流模型（式（9））所含的3个工艺参数与能耗的关系曲线，对其中任意一个参数作图时，另外两个参数固定为常数，结果见图7～图9。其中，a5是一个与变形抗力有关的系数，-p为平均单位压力。

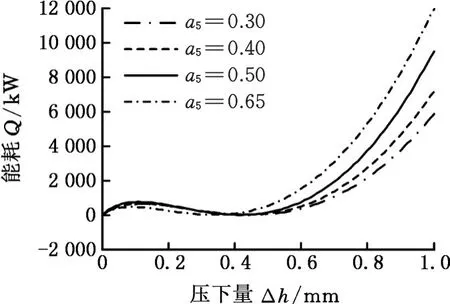
图7 压下量与能耗的关系Fig.7 Relationship between Δh and Q

图8 轧制速度与能耗的关系Fig.8 Relationship between niand Q

图9 平均张力与能耗的关系Fig.9 Relationship between q and Q

由图7可知，当固定速度和平均张力时，压下量在某一段范围内有一极小值点0.4 mm（该极小值由于参数人为固定和人为设定，故无实际意义），在极小值点附近轧制能耗随压下量增大先增大再减小，在此之后又继续增大，正好对应表2中最优压下量0.15 mm。由此得出，冷轧单个机架能耗随着压下量从0增大，会经历一个极小值点，满足约束的最优压下量在极小值点附近。由图8可知，轧制速度越大，轧制能耗越大，增大的速率受其他参数影响。由图9可知，随着平均张力增大，轧制能耗呈线性降低，降低的速率与其他参数无关，符合表2中的优化结果。本文的实例只分析了一种钢，而实际冷轧生产接近多品种小批量生产，带钢的品种达上千种，各钢种的能耗极小值点也不固定，因此在实际的能耗优化中，应建立工艺数据库，随时读取数据计算。

本文建立了轧制功率与压下量、轧制速度、平均张力之间的数学模型，采用改进的粒子群算法对模型中的3个工艺参数进行优化求解。从表2中的数据可以看出，3个工艺参数最终趋于固定值以使轧制功率最优，这说明提出的模型是合理和可靠的，同时说明使用引入非线性权重系数递减策略的粒子群算法在寻优时具有良好的收敛性，适用于单个机架的工艺参数优化研究。

4 结论

本文针对机组众多、工艺参数复杂的酸洗连轧生产线，建立了功率模型，并以轧机机架和酸洗槽为典型例子进行了分析。模型可以通过给定钢卷的工艺参数给出各工艺所需功率。通过代入实际参数后计算轧制功率，与冷轧厂提供的电机容量进行对比，对模型进行校核。根据建立的能量流模型，利用改进的粒子群算法，对模型中的压下量、轧制速度和平均张力3个工艺参数进行优化求解，得出了最优工艺参数存在的范围。后续的研究将进一步针对冷轧的镀锌、连退、精整等工艺开展能量流建模，并继续优化冷轧产线能耗。