复合材料开口有限元建模方法研究
2020-08-12熊美蓉陈琳刘传军
熊美蓉,陈琳,刘传军
(1.中国商飞上海飞机制造有限公司,复合材料中心,上海 200123;2.中国商飞北京民用飞机技术研究中心,民用飞机结构与复合材料北京市重点实验室,北京 102211)
0 引言
复合材料开口产生的局部应力集中会引起结构强度下降,应力集中与层压板铺层比例、载荷情况、缺口尺寸和形状、缺口约束情况有关。
在比较主流的分析方法中,对于单轴载荷下复合材料开口结构,可采用基于断裂力学模型Mar-Lin准则[1]进行层合板剩余强度分析,将开口定义为损伤,通过获得不同铺层下的复合材料断裂韧性、奇异性参数、构型因子等,拟合得到不同开口尺寸下的层合板剩余强度;另一种方法是采用基于应力失效模型的Withney-Nuismer方法[2],获得圆孔层合板在圆孔中心线上垂直于远场载荷方向的应力分布,再通过点应力或平均应力方法开展失效分析。对于复杂载荷下,可采用Lehknitskii理论[3]中提出的复变函数计算含椭圆孔(圆孔)的正交各向异性无限大板,在复杂远场载荷作用下的孔边应力分布,再通过点应力或平均应力方法开展失效分析。
常见的飞机复合材料开口结构和其载荷状况都较为复杂,一般采用精细有限元建模后提取孔边最大应力或应变开展分析。而开口区的复杂应力分布对孔边网格要求较高,网格尺寸、数量和质量等都会直接影响数值计算的结果精确性,同时网格尺寸过小也影响计算效率。本文主要研究复合材料开口结构在单轴和双轴两种载荷状态下复合材料开口结构孔边网格尺寸对有限元计算精度的影响,为开展复合材料开口有限元建模和分析提供指导。
1 单轴载荷分析
本文选用T800级碳纤维复合材料开口层合板,其铺层为[45 °/135 °/0 °/90 °/90 °/0 °/135 °/45 °],层合板为100 mm× 100 mm 方板,圆孔直径为25.4 mm,主要分析层合板单轴载荷作用下,孔边的应力应变分布情况。
1.1 分析方法
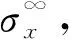
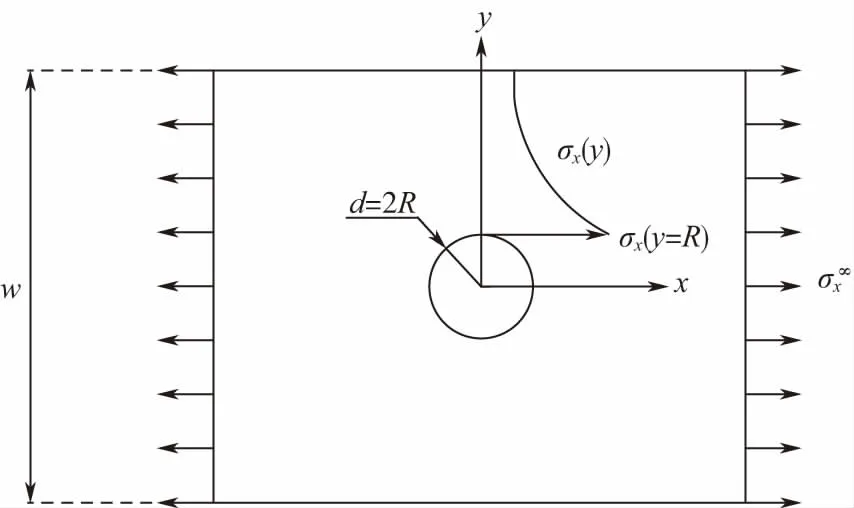
图1 在单向拉伸作用下、含圆形孔开口区应力分布示意图
对有限宽板,沿y轴方向的应力σx(y)表达式:
(1)
(2)
其中β为有限宽度修正系数,修正系数根据材料(各向同性和各向异性)和开口类型(圆孔或椭圆孔)变化;KT为孔的应力集中系数。
1.2 孔边应力计算
采用1.1节中Withney-Nuismer方法计算在100 MPa沿X轴作用下,层合板孔边沿Y轴的应力分布。
图2 孔边Quad单元与节点示意图
当采用四节点的Quad单元划分有限元网格时,对模型求解得到的孔边最大应变,即为孔边一圈所有单元中的最大应变。如图2所示,可通过节点位置处的应变估算得到001单元的应变值,计算图中1、2、3、4节点位置处应变的平均值,作为单元的中心点的应变,这样即可预测不同有限元网格尺寸下孔边的最大应力和应变。
取开口直径为25.4 mm的复合材料层合板,计算网格大小为0.000 1 mm、0.001 mm至10 mm时,孔边单元对应的最大应力、最大应变及相对于孔边最大值精确解的误差(表1)。从图3中也可以看出,开口直径为25.4 mm时,当网格尺寸在0.000 1 mm到0.01 mm时,孔边的最大应变趋于收敛,精度不超过0.1%。随着网格尺寸增大,孔边最大应变略微下降,计算精度也逐渐降低。
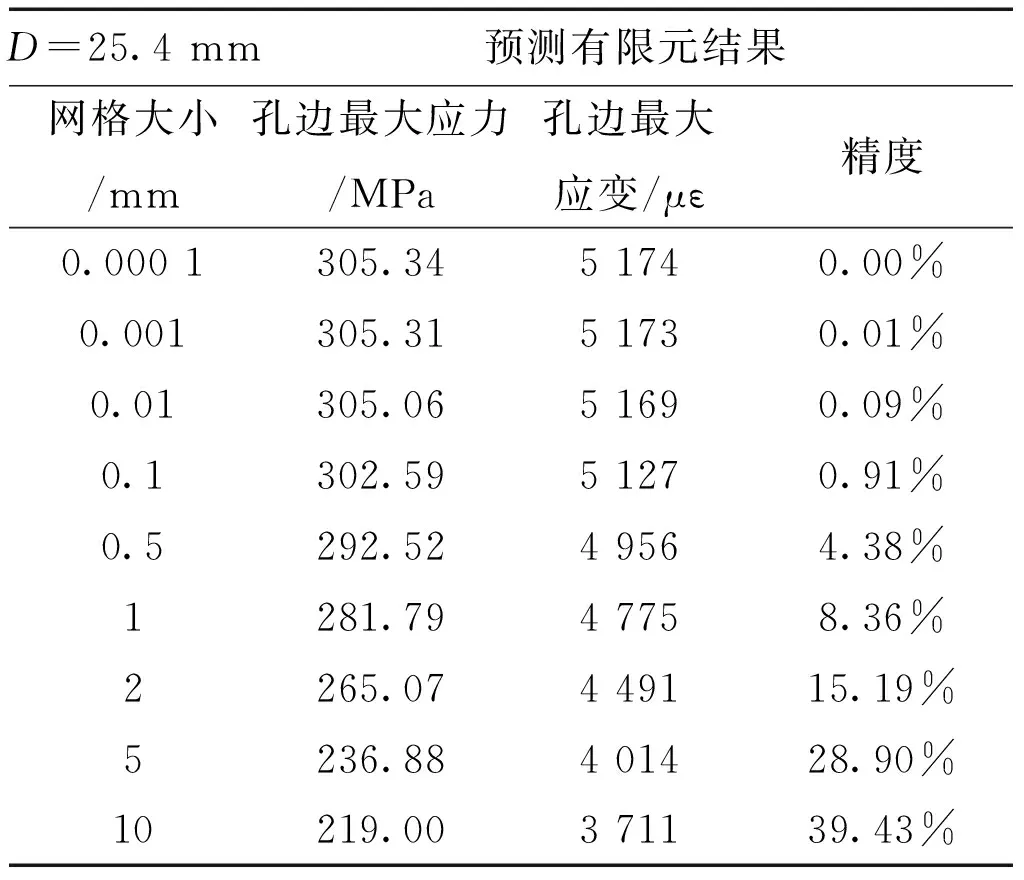
表1 单轴载荷网格尺寸对计算精度的计算
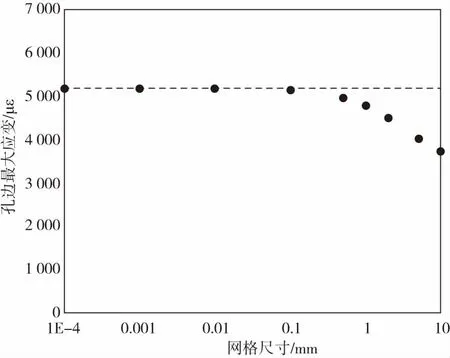
图3 不同开口区网格尺寸对孔边最大应变的影响
1.3 开口尺寸及铺层影响
从Withney-Nuismer方法的解析公式可以看出,孔边应力分布主要是开口尺寸与层合板铺层的函数,根据1.1中对有限元模型中孔边最大应力应变的估算方法,可以分析不同开口直径下不同网格尺寸的精度大小。如图4所示,图中曲线为针对准各向同性层合板开口直径分别为6.35 mm、12.7 mm、25.4 mm、50 mm、100 mm及200 mm下不同网格尺寸下的精度大小。可以看出,开口直径越小时对孔边网格大小越为敏感,对较小直径如6.35 mm的开口,孔边网格为0.1 mm时,最大应变精度为3.54%,而较大直径下200 mm的开口,孔边网格为0.1 mm时,最大应变精度依然较高为0.58%。当直径大于100 mm后,孔边网格小于1 mm可获得5%以上的精度。
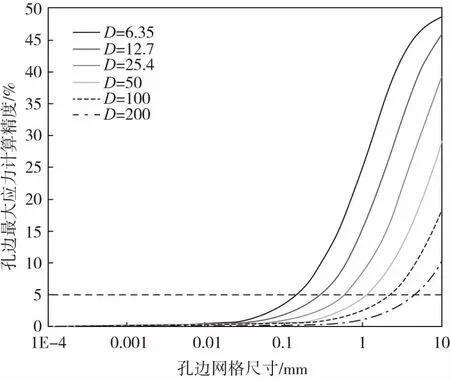
图4 单轴载荷不同开口直径下网格尺寸对计算精度的影响
复合材料层合板铺层主要影响孔边应力集中系数,从而影响孔边应力应变分布。图5主要分析了四种铺层比例下不同网格尺寸的精度大小。对于开口直径为25.4 mm的层合板,当AML(AML=±45 °铺层百分比-0 °铺层百分比)越小,即0 °铺层比例越高时对孔边网格大小更为敏感。对绝大多数铺层,在孔边网格尺寸在0.01 mm时精度可以控制在0.21%以下。相对于开口尺寸,铺层的影响要较小一些,因此可以主要根据开口直径和精度要求估算出孔边网格大小,再针对铺层作简单分析来确定有限元模型网格划分,以满足强度计算要求。
2.2.5 水煎煮提取工艺正交试验 根据上述的药效筛选结果,对水煎煮提取工艺进行正交试验,以君药黄芪中黄芪甲苷含量(Y1)和固形物质量(Y2)为评价指标,并分别赋予权重系数0.6和0.4,计算综合评分值[Y,Yi=(X1i/X1max×0.6+X2i/X2max×0.4)×100],对影响煎煮的加水量(A)、煎煮时间(B)和煎煮次数(C)进行优选。因素与水平见表3。

图5 单轴载荷不同铺层比例下网格尺寸对计算精度的影响
2 双轴载荷分析
本文选用T800级碳纤维复合材料开口层合板,其铺层为[45 °/135 °/0 °/90 °/90 °/0 °/135 °/45 °],层合板为100 mm× 100 mm 方板,圆孔直径为25.4 mm,主要分析在双轴应力100 MPa作用下,孔边的应力应变分布情况。
2.1 分析方法
双轴载荷下开口分析采用Lehknitskii方法,Lehknitskii模型如图 6所示。分析假设如下:
(1)材料主轴方向12与椭圆孔主轴方向xy一致。
(2)平板尺寸与椭圆孔或者圆孔尺寸相比可认为是无限大。
(4)考虑平面应变或者广义平面应力情形。

图6 在远场力作用下、含开口的无限大平板
孔缘的应力由远场应力和扰动应力构成,形式如下,
(3)
(4)
式中:Re——复数的实部;
Zk——复数变量,形式为Zk=x+yμk(k=1,2);
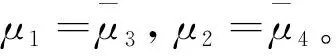
Φk(Zk)为复应力函数, 由椭圆孔存在引起的扰动应力对应的应力函数为:
(5)
2.2 孔边应力计算
根据2.1中对有限元模型中孔边最大应力应变的估算方法,取开口直径为25.4 mm的复合材料层合板,采用Lehknitskii方法,计算复合材料开口层合板在计算在X轴远场载荷100 MPa与Y轴远场载荷100 MPa作用下,网格大小为0.000 1 mm、0.001 mm至10 mm时,孔边单元对应的最大应力、最大应变及相对于孔边最大值精确解的误差。从表2中也可以看出,对于开口直径为25.4 mm时,当网格尺寸在0.000 1~0.01 mm时,孔边的最大应变趋于收敛,精度不超过0.1%,与单轴载荷趋势一致。
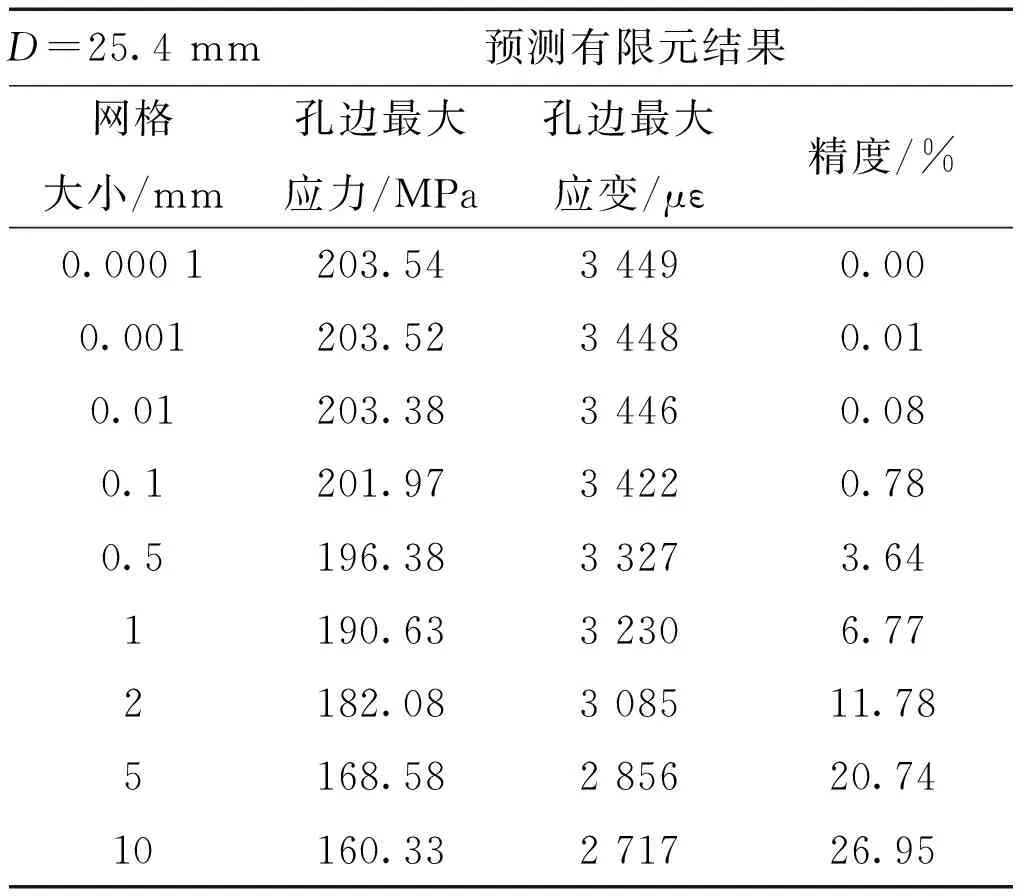
表2 双轴载荷网格尺寸对计算精度的计算
2.3 开口尺寸及铺层影响
在双轴载荷下,复合材料层合板开口孔边的应力应变分布受铺层影响较大。对于25 °/50 °/25 °准各向同性铺层的层合板,在100 MPa、100 MPa双轴载荷作用下,其0~180 °孔边的应力分布如图7所示,可知最大主应力出现在孔边0~360 °所有方向上。而对于纯±45 °铺层层合板,在100 MPa、100 MPa双轴载荷作用下,其0~180 °孔边的应力分布如图8所示,可知最大主应力出现在孔边45 °、135 °、225 °、275 °方向。此外,应力应变分布还与x轴、y轴载荷比例有关,本文暂不做具体分析。
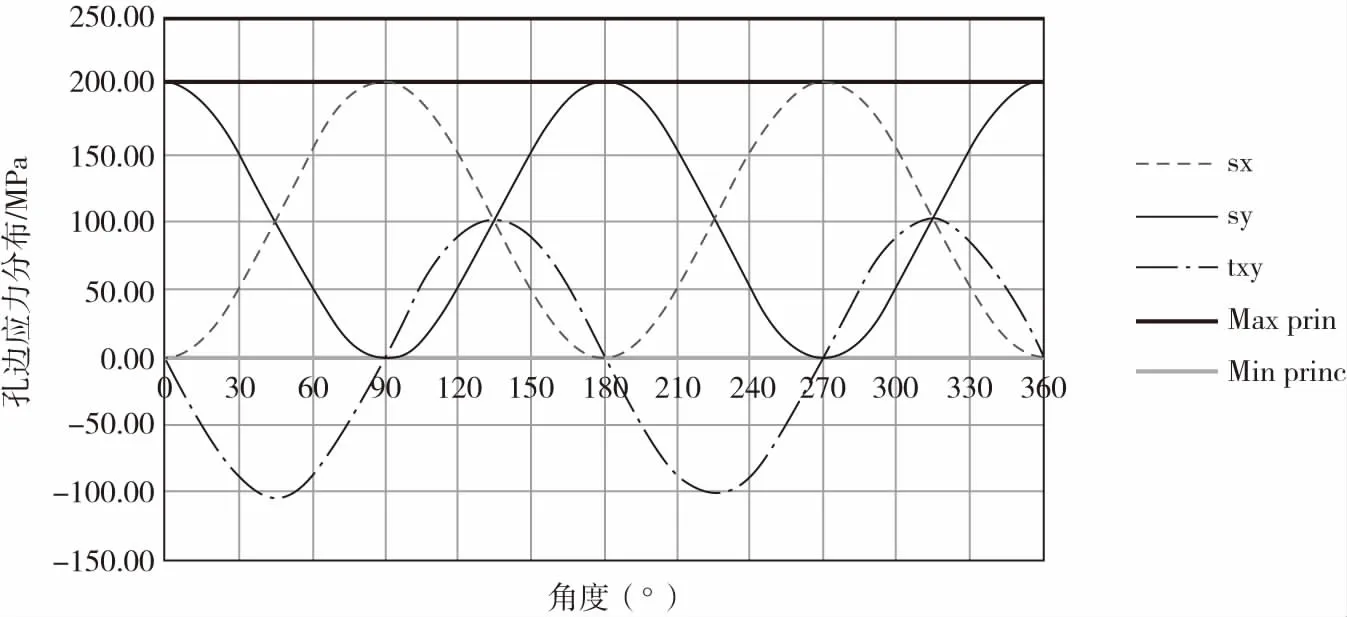
图7 准各向同性层合板孔边应力应变分布(σx ∶σy=1 ∶1)
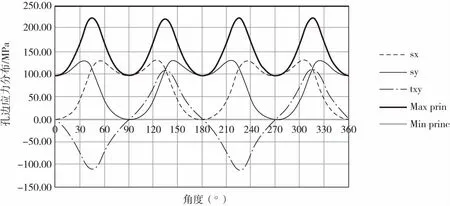
图8 纯±45 °铺层层合板孔边应力应变分布(σx ∶σy=1 ∶1)
根据2.1中对有限元模型中孔边最大应变的估算方法,可以分析不同开口直径下不同网格尺寸的精度大小。如图9所示,图中曲线为针对双轴载荷下的准各向同性层合板,开口直径分别为6.35 mm、12.7 mm、25.4 mm、50 mm及100 mm下不同网格尺寸下的精度大小。可以看出,开口直径越小时对孔边网格大小越为敏感,对较小直径如6.35 mm的开口,孔边网格为0.1 mm时,最大应变精度为3.54%,而较大直径100 mm的开口,孔边网格为0.1 mm时,最大应变精度依然较高为0.58%。当直径大于100 mm后,孔边网格小于1 mm可获得5%以上的精度。相比于单轴,不同开口直径层合板在双轴载荷下精度略高,主要原因是层合板的泊松效应一定程度降低了孔边的应力集中,应力分布受网格尺寸的影响也略为降低。
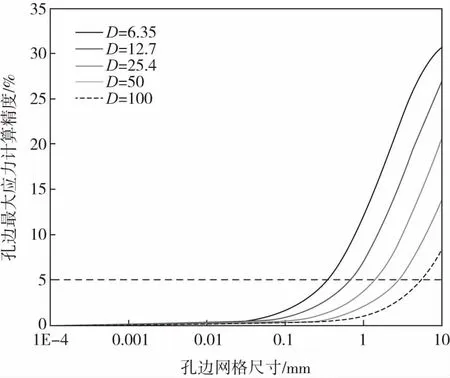
图9 准各向同性层合板不同开口直径开口网格尺寸对孔边最大应力的影响(σx ∶σy=1 ∶1)
采用同样方法,对双轴载荷下的纯±45 °铺层层合板开展分析,取45 °方向最大应力,分析不同开口直径下不同网格尺寸的精度大小如图10所示。可以看出,与前文中分析结果一致,开口直径越小时对孔边网格大小越为敏感。当开口直径为6.35 mm和12.7 mm层合板时,图中可明显看出,当网格尺寸>1 mm后曲线出现拐点,主要原因为±45 °铺层层合板在x,y轴双轴加载时,沿着45 °方向离孔中心超过5 mm后,应力有所升高,如图11所示。

图10 纯±45 °铺层层合板,不同开口直径开口网格尺寸对孔边最大应力的影响(σx ∶σy=1 ∶1)

图11 纯±45 °铺层层合板,E11随距离孔边位置变化趋势(σx:σy=1 ∶1)
通过对比两种铺层下不同开口的精度分布,可发现纯±45 °铺层相比准各向同性铺层对孔边网格尺寸更为敏感,且铺层比例影响孔边最大应力点的分布位置。因此对双轴载荷的复合材料开口结构建模时,需按实际铺层进行估算,以确定有限元模型网格划分,以满足强度计算要求。
3 有限元网格尺寸
为验证上述分析方法,本文在ABAQUS CAE中建立了复合材料开口结构有限元模型,定义载荷和边界条件,对模型网格划分,并对孔周边网格进行细化。图12与图13分别为准各向同性铺层层合板在双轴载荷下的孔边最大主应力和最大应变的分布云图。在最大主应力的分布云图中可知,孔边最大主应变为3 466ε,E11方向最大应变为3 458ε,与解析法计算的E11最大应变相差9ε,偏差在0.26%。
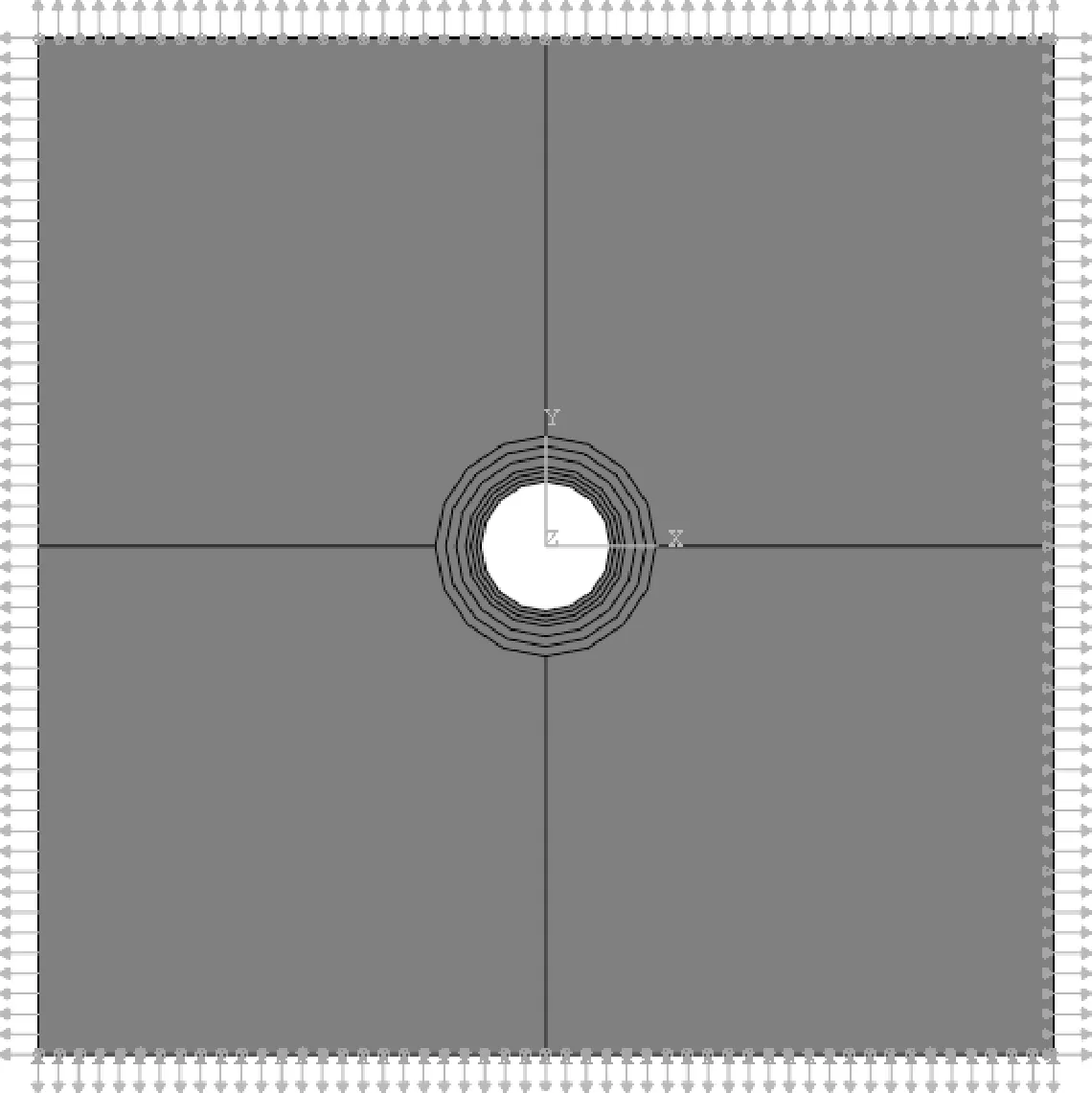
图12 复合材料开口结构双轴加载有限元模型

图13 复合材料开口结构双轴载荷的最大主应力和最大应变分布云图
本文同时开展了单轴载荷下有限元方法、Withney-Nuismer方法和Lehknitskii方法计算结果的对比,如图14所示。从图14可看出,解析解和数值解的计算结果一致性较好,有效验证了解析方法计算的合理性。
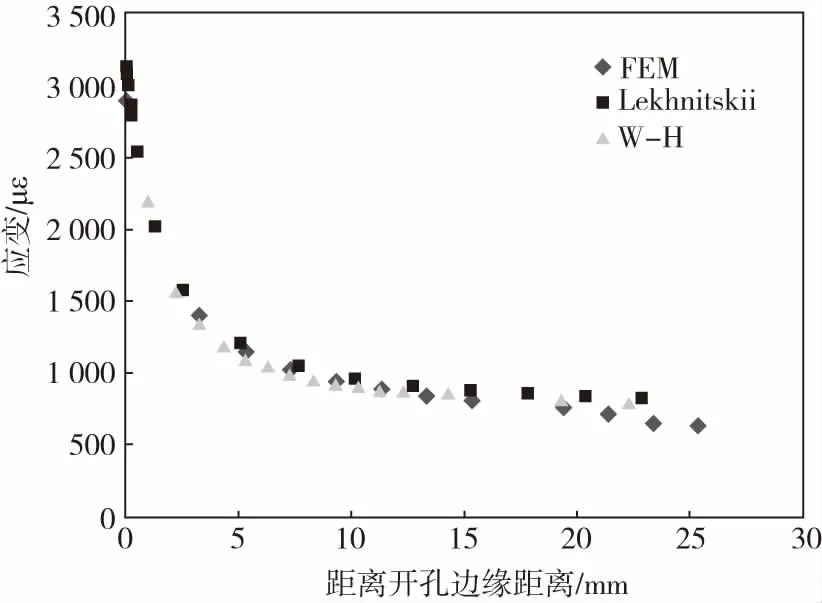
图14 有限元方法和解析法计算结果对比
4 结论
本文通过研究复合材料开口层合板在不同载荷状态、开口尺寸及铺层比例下,有限元网格尺寸与数值计算精度的关系,通过分析,得到如下主要结论:
(1)在单轴载荷下,开口直径越小时对孔边网格大小越为敏感,0 °铺层比例越高时对孔边网格大小更为敏感。对开口直径25.4 mm、大多数铺层的层合板,在孔边网格尺寸0.01 mm时精度在0.21%以上。
(2)在双轴载荷下,开口直径越小时对孔边网格大小越为敏感;相对单轴载荷,存在一定泊松效应降低应力集中,降低网格敏感度。孔边最大应力位置与铺层比例和载荷状态相关。
