轻量化设计中的NVH性能自动优化方法

王 磊，王学智

（爱驰汽车有限公司，上海 200082）

汽车轻量化设计是一个重要的研究方向，在汽车轻量化研究过程中，会给众多性能的优化带来更多的困难和要求，在满足同样或更好的性能指标的同时还要减轻质量，因此多学科联合优化显得更加重要。

目前多学科联合优化设计已被广泛应用在汽车设计领域，最具代表性的是兼顾车身刚度、模态、碰撞性能的轻量化设计。但多数关于轻量化和多学科联合优化的文献，在对NVH性能的自动优化过程中，只考虑了模态这一单一指标，并未考虑动刚度、噪声传递函数（Noise Transfer Function，NTF）和振 动传 递函 数 （Vibration Transfer Function，VTF）等性能指标[1-8]。研究表明，在自动优化过程中，如果只考虑刚度和模态性能，可大幅减轻车身质量；如果只考虑各种碰撞性能，轻量化的效果下降，但可以通过材料优化提升其效果；如果只考虑动刚度、NTF、VTF等NVH性能，轻量化效果会大打折扣[9]。因此，轻量化设计过程中，NVH性能指标成为短板，需要进行自动化的全局优化。

以某白车身模型的零件厚度为设计变量，以针对动刚度性能进行轻量化优化为例，介绍了在轻量化设计过程中的NVH性能自动优化方法。NTF与VTF性能的自动优化方法与之相同，只是作为约束条件的响应点数量不同，因此不再累述。该方法可与车身模态、刚度等其它性能的自动优化流程[10]联合使用，实现多学科联合优化并减轻质量。

1 模型描述

白车身动刚度分析模型中共有32个不同位置的加载点，如图1所示，每个加载点分别施加x、y、z三个方向的1～250 Hz激励，读取每个方向激励下所对应的加载点在加载方向上的响应，则每个模型状态会有96条曲线作为考察指标。

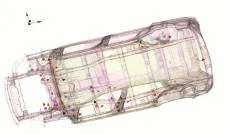
图1 分析模型

如果对NTF和VTF进行分析，需要读取每个方向激励下多个测量点在x、y、z三个方向上的响应，则每个模型状态下作为考察指标的曲线将会更多。

2 结果评估准则

NVH性能自动化优化需要以合理、可行的评估准则为基础。将每条曲线在50～250 Hz范围内分成4段，每段的平均值作为一个评价指标，则分析白车身动刚度时将有384个数值评价指标。

多目标优化问题的数学模型可描述为：

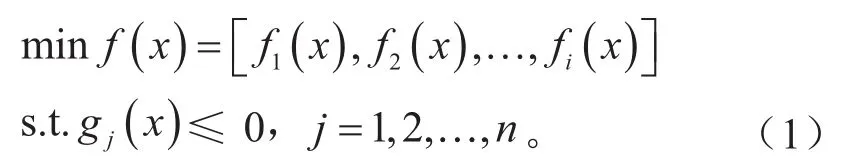
式中：f(x)为目标函数；g(x)为约束条件。将所有考察点的评价指标设为约束，仅质量设为目标，使复杂的多目标优化问题转化为简单的单目标优化问题。

不考虑轻量化的NVH性能优化中，每个指标只需要跟目标值进行比较，其评估结果有两种或三种状态：满足要求（绿）、不满足要求（红），或者再增加一个接近目标值可接受的状态（黄）。而在轻量化设计过程中的NVH性能优化，不仅需要将每个评价指标与对应的目标值比较，还要跟初始结果进行比较。在满足目标值要求的情况下，即使性能大幅下降，也是可接受的结果；而在不满足目标值要求的情况下，如果性能下降的幅度较小，仍是可接受的结果，评估的总体原则如图2所示。

点对多点的传输模式，主要是为了方便配置和合理的应用，在网络中设置了服务器和客户端的概念，而且存在主备切换。雷达设备通过不时地向空中发送检测数据，将收集到的数据发送到雷达数据处理机，再通过雷达数据接收机将同步数据通同步数据端口发送至FA16-T设备，FA16-T设备在TCP/IP通过广播的方式发送至远端的多台FA16-T设备，再分别传送至多个雷达自动化系统，最后由管制人员在终端上监控雷达数据。

图2 评估标准

3 近似模型精度

任意选取70个零 件的厚度作为变量，如图3所示，其中对称的两个零件为一个变量，共40个变量。使用iSIGHT软件通过计算试验设计（Design of Experiments，DOE）样本，建立近似模型，使用近似模型进行单目标优化的方法进行优化。

图3 作为优化变量的零件

研究的重点在于近似模型的建立，只有保证近似模型有足够的精度，才能准确判断NVH性能的结果，进而得到有效的优化结果。采用Optimal Latin Hypercube方法生成DOE样本，实践证明针对40个变量的规模，若要保证有足够的精度，800个以上的样本是必须的。

经长期的试验和测试后，对于上述问题，除神经网络模型外，Kriging模型、正交多项式模型、响应面模型（包括多阶响应面模型）均无法建立高精度的数学近似模型。

神经网络模型中的椭圆基函数（Elliptical Basis Function，EBF）类似径向基函数（Radial Basis Function，RBF）。但其用椭圆单元代替径向单元，相比于RBF，对所有输入处理都相同，只是EBF使用独立的权重分别处理每个输入。RBF神经网络的特点是训练速度快，EBF神经网络则需要更多的迭代来学习单个输入的权重，所以比RBF更耗时但更准确。

使用EBF神经网络模型建立近似模型，为证明结果的真实性，原始计算结果数据及近似模型已公开，见参考文献[11]（提取码：WANG）。使用10个随机样本检验模型的精度见表1。

表1 近似模型精度

4 性能优化

按照图4所示的判断流程，将评估准则转化为计算机程序：

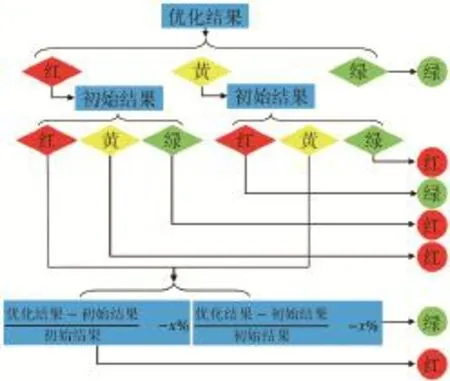
图4 评估及计算机判断流程

iSIGHT软件中独有的Pointer算法是一种复合型数值搜索方法，将遗传算法、下山单纯形法、序列二次规划和线性搜索算法自动组合，在绝大多数情况下，是搜索全局优化解效率最高的算法之一，但是在个别情况下的效果却不理想。此外，自适应模拟退火法（Adaptive Simulated Annealing，ASA）也是效率较高的优化算法，尤其是在解决高度非线性问题和寻找全局最优解方面。

Hooke-Jeeves 模式搜索法相对来说在优化求解中被用到的不多，该优化算法不需要目标函数，它用目标和约束的罚函数作为目标函数。该算法从初始基点开始，进行两种类型的移动——探测移动和模式移动。探测移动的目的在于确定更好的基点和收敛方向，模式移动的目的在于寻找极值[12]。虽然该算法的理论介绍说明其用于无约束优化问题，且不适用于非连续的设计空间和变量较多的模型，收敛速度慢，然而对于动刚度性能的优化无论是在效率还是效果方面却都很出色。

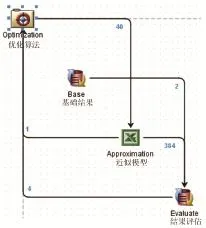
图5 优化流程

基于iSIGHT优化平台软件的优化流程如图5所示。首先，创建Base数据处理区域，用于存放初始模型的计算结果和目标值；然后，利用Excel组件读入EBF神经网络法所建立的近似模型，设置与原始有限元模型完全相同的输入和输出条件；建立Evaluate结果对比评估区域，通过与Base和Approximation之间建立映射关系，传递初始模型和优化模型的计算结果，通过上述评估准则和计算机程序对其进行比较和评估，将评估结果输出给优化主程序；由优化主程序控制Approximation中的变量更改，得到Approximation返回的质量结果和Evaluate返回的动刚度性能评估结果之后，选用不同的优化算法进行迭代优化，寻找全局最优解集。

不同的约束条件和优化算法必然得到不同的优化结果。约束条件为动刚度性能降低5%以内时，使用各优化算法得到的结果见表2（结果在小范围内具有一定的随机性）。

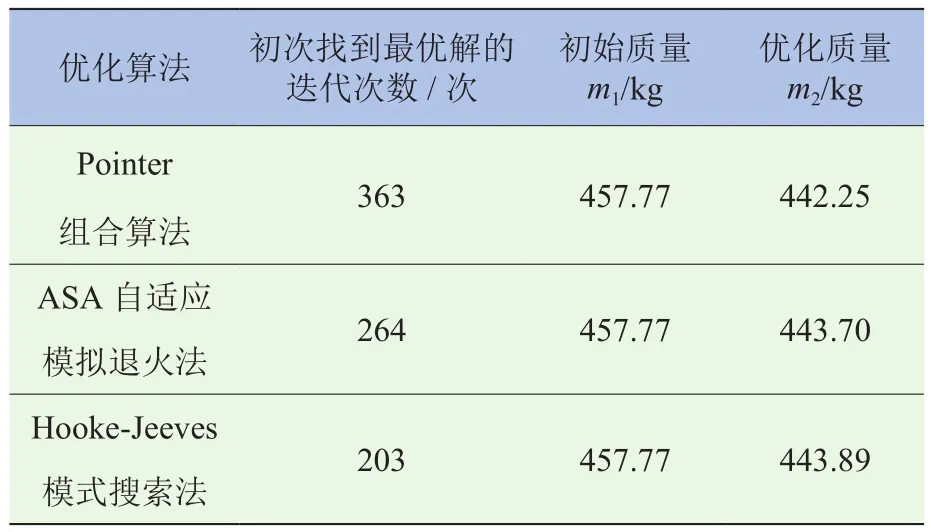
表2 以性能降低小于5%为约束条件的优化结果

由表2可知，当以动刚度单一性能为约束条件，且允许性能降低5%以内时，使用Pointer优化算法可以减轻质量15.52 kg。

给出初次找到最优解的迭代次数的意义在于说明：在搜索全局最优解的过程中，当前时刻根本无法确定其是否为全局最优解，进而需要继续搜索，最后往往需要其几倍甚至十几倍的迭代次数，才能确定已搜索范围内的最优解集。因此，对于所列举的此类优化问题，无论是时间效率方面，还是获取优化结果的保障性方面都不适合使用直接寻优方法，而是需要通过数学模型进行优化。

约束条件为动刚度性能降低1%以内时，使用其它优化算法可能无法收敛，得不到满足要求的减轻质量的结果。使用Hooke-Jeeves算法得到的结果见表3。

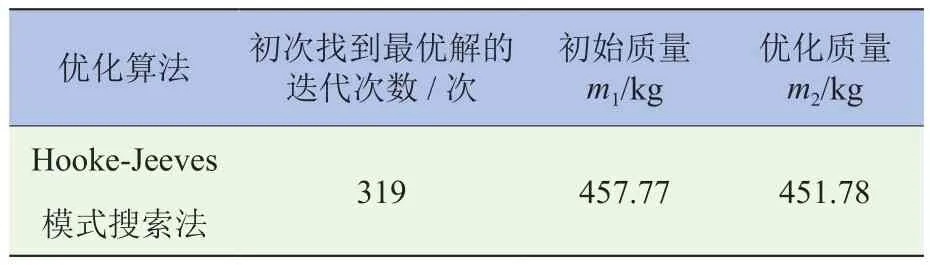
表3 以性能降低小于1%为约束条件的优化结果

当以动刚度单一性能为约束条件，且允许性能降低1%以内时，使用Hooke-Jeeves模式搜索优化算法可以减轻质量5.99 kg。

5 结论与展望

（1）以基于厚度变量的动刚度自动优化方法为例，介绍了在轻量化设计过程中NVH性能的自动优化方法，通过高精度的近似模型和不同的优化算法获得了很好的减轻质量的效果，最终的厚度参数优化方案全部符合工艺要求。可以有效避免在自动优化过程中只考虑刚度、模态、碰撞性能，获取优化结果之后，再对其它NVH性能进行手工验证而导致的质量减轻较少甚至几乎不会减轻的情况。

（2）复杂优化问题由于搜索迭代次数较多，不宜使用直接寻优的方法。由于约束条件的设定可能导致无法获取优化结果的情况，也不宜使用直接寻优的方法。使用数学模型进行优化，可以保证在项目的实际应用过程中，在一定的时间范围内，能够获取相对较佳的减轻质量的方案，避免出现得不到任何优化结果的情况而影响项目进度和质量。

（3）该方法的进一步研究可联合SFE Concept软件进行几何参数的NVH性能自动优化。

（4）基于该方法的进一步研究，可用于高精度的碰撞性能自动优化，进而实现真正意义上的多学科联合自动优化。