基于混沌RBF神经网络的汽油机点火提前角预测
2018-10-22刘东阳李岳林刘博夫
刘东阳,李岳林,葛 进,刘博夫,张 银
(长沙理工大学,长沙 410076)
目前,汽油机上通常采用传统的插值方法确定点火提前角,插值法实现简单、计算速度较快,但精度较低。此外,由于制造误差、使用磨损,以及汽油机在实车上与试验台架上运行存在差异,试验确定的点火提前角对同型号的其它汽油机未必是最佳。张晟恺等[1]采用 BP 神经网络对点火提前角进行训练,根据训练过后得到的权值和阀值,达到预测发动机点火控制的目的。王彦岩等[2]通过试验获取的点火提前角标定试验数据作为样本数据,对RBF神经网络进行训练,建立了基于RBF神经网络的汽油机基本点火提前角预测模型。虽然以上点火提前角预测控制精度都得到了提高,但BP神经网络存在容易陷入局部极小点、收敛速度慢等缺点,其预测精度难以达到预期效果。混沌运动具有不稳定性、规律性和遍历性等特点,神经网络学习规则简单,能够处理系统内在的规律性,具有很强的非线性映射能力鲁棒性以及强大的自学习能力。因此,利用混沌预测算法与神经网络相结合的方法,建立混沌RBF神经网络模型对点火提前角进行预测。仿真结果验证了混沌RBF神经网络模型比BP神经网络模型、传统插值法具有更强的非线性预测能力,实现神经网络的学习全局最优,点火提前角预测精度得到了显著提高。
1 混沌序列预测理论
在混沌动力学中,TAKENS提出的相空间重构理论是重构具有混沌特性的时间序列成一种低阶非线性动力学系统,从而原有系统的混沌吸引子得到近似恢复[3]。汽油机是一个多维非线性动力学系统,可将点火提前角预测问题转化为在相空间中一个短期演变过程来进行研究,为点火提前角混沌时间序列预测提供了前提条件。
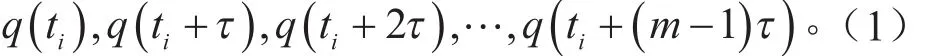
式中:Δt为采样间隔;k为整数;τ=kΔ t为延滞时间。n个相点间的连线描述了m维相空间的演化轨迹,任一相点有m个分量,每一列构成m维相空间的一个相点,相点数n=N −(m−1)τ[4]。
运用文献[5]中所述的C-C方法计算最大Lyapunov指数,判断该系统时间序列具有混沌特性。通过快速傅里叶变换(FFT)计算时间序列的平均周期,而时间序列的平均频率就是后能量加权平均的频率,其倒数即为平均周期。利用上述C-C方法自动搜索式(3)的第一个极小值,即寻找时间序列独立的第一个局部最大值。
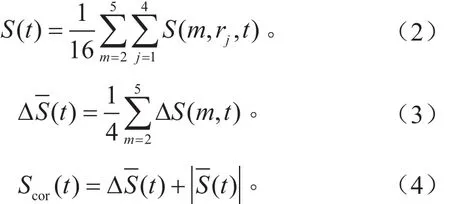
通过式(4)的最小值去获取时间序列独立的第一个整体最大值时间窗口τw=tτs,τs为时间序列的采样间隔,求得τw=14,τ=2,因此时间延迟为2d(d是混沌吸引子的关联维数),再由式(5)计算出相空间重构的嵌入维数为m=8。

然后根据式(6)重构相空间qj, j = 1, 2,… ,M中每一个点ri最邻近点Gauss。
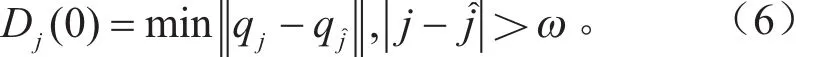
式中:ω=T/Δt,Δt为序列的采样周期。
根据式(7)对该邻点qj在i个离散时间步后的距离Dj(i),可由重构相空间qj, j = 1, 2,… ,M 中每个点qj计算得出。

式中:i=1, 2,… ,min(M − j, M − j^ )。
假设第i个点的最邻近点近似于以最大的Lyapunov指数速率发散,即:

式中:Ci指初始的分离距离常数。对式(8)两边同时取对数,即方程代表一簇斜率为λi近似平行线。
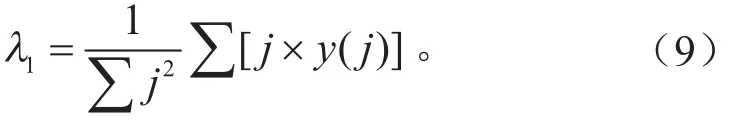
式中:为非零nDi( j )数目。
用以上方法求得,相空间重构的嵌入维数为m= 8 , τ = 2 , τw=14,计算得到最大Lyapunov指数λ1稍大于0,表明该时间序列具有混沌特性,可针对汽油机点火提前角进行短期预测。
2 混沌RBF神经网络点火提前角模型
RBF神经网络[6]是一种三层前向神经网络,输入层到隐层单元之间为直接连接,隐含层到输出层之间为权连接。RBF神经网络的自变量为输入模式与中心向量的距离,采用径向基函数(如Gauss函数)作为激活函数,可映射任意复杂的非线性关系,学习规则简单,具有很强的自学习、非线性拟合能力,RBF神经网络的表达式如下,其结构如图1所示。
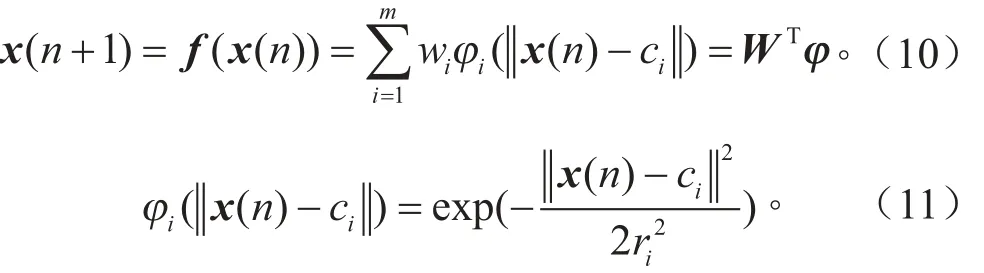
式中:x(n)为输入向量,x( n ) ∈ Rm;f为输出向量,f∈R1;ϕi(•)为Gauss函数; ϕ==[ϕ1, ϕ2,…,ϕm]T为隐含层输出向量;W=[w1, w2,…,wm]T为神经网络输出层的权值向量,m为隐含层单元的个数;ci和ri分别为Gauss函数的中心和宽度[7],i = 1, 2,…,m。以wi和ci作为混沌变量,采用Logistic映射混沌模型,运用混沌算法优化RBF神经网络,使其收敛速度更快,达到全局最优。
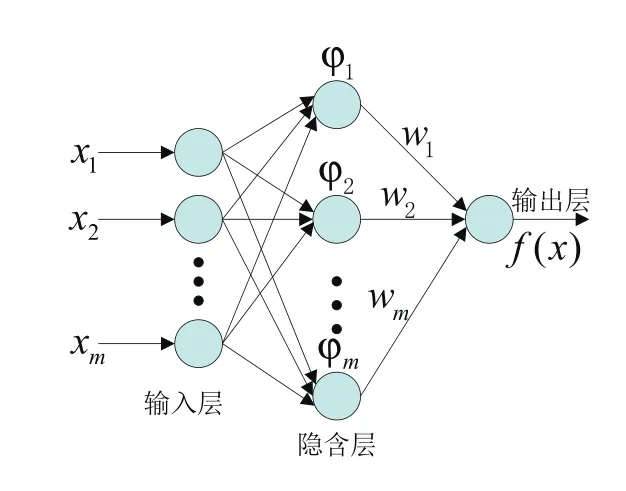
图1 RBF神经网络的结构图
点火提前角的影响因素相对较多,其中有发动机转速(转角)ω、负荷(进气歧管压力Pa)、空燃比A/F、节气门开度ρ、冷却水温度Tm等,而且此类因素都具有随机性、非线性、分散性的特点。转速(转角)ω和负荷(进气歧管压力)Pa是预测点火提前角的两个关键参数,冷却水温Tm等通常是点火提前角的修正因素,只有在精确获取了转速和负荷这两个参数的情况下,才能对点火提前角进行有效的预测。因此,将发动机转速和负荷作为神经网络的输入,所对应的点火提前角作为神经网络的输出。
发动机模型采用 Elbert Hendrieks模型,它是用数个发动机循环中变量的平均值来描述发动机的动态过程,是目前最为常用的模型[8-9]。利用混沌算法优化RBF神经网络的权值和阈值,建立混沌RBF神经网络点火提前角预测模型,使其成为混沌动力学系统。所建立的混沌RBF神经网络点火提前角模型原理如图2所示。图中:U表示喷油脉宽;θ为混沌RBF神经网络所预测点火提前角;ω、Pa、Te和 λ 分别为发动机的转速(转角)、负荷(进气歧管压力)、转矩和空燃比。
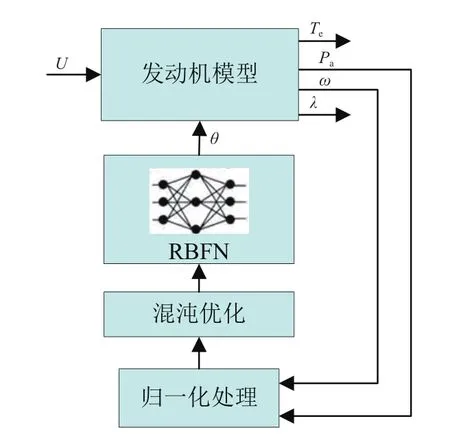
图2 混沌RBF神经网络点火提前角模型原理
3 试验标定与仿真
以发动机的转速(转角)和负荷为对点火提前角的关键影响因素,采取试验标定和软件仿真相结合的方法,验证混沌RBF神经网络预测值的准确性。标定试验在EA113发动机台架上进行,表1为台架试验所用发动机的主要性能参数。
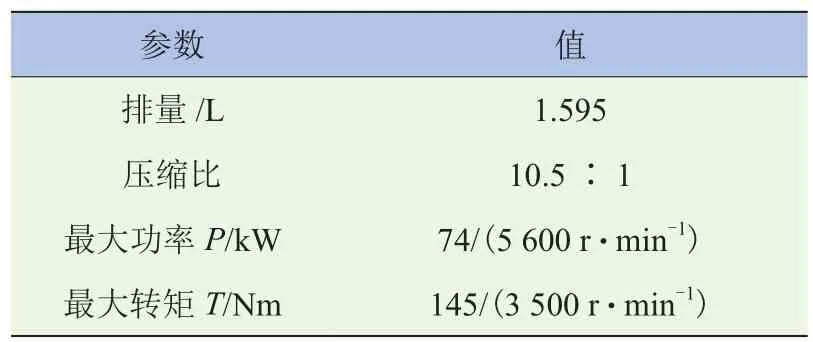
表1 EA113发动机主要技术参数
标定试验所得结果见表2。在不同负荷下,转速为1 600 r/min、2 800 r/min和4 000 r/min作为混沌RBF神经网络测试样本,检验模型的准确性,其余标定数据作为训练样本。基于以上数据,点火提前角MAP图如图3所示。
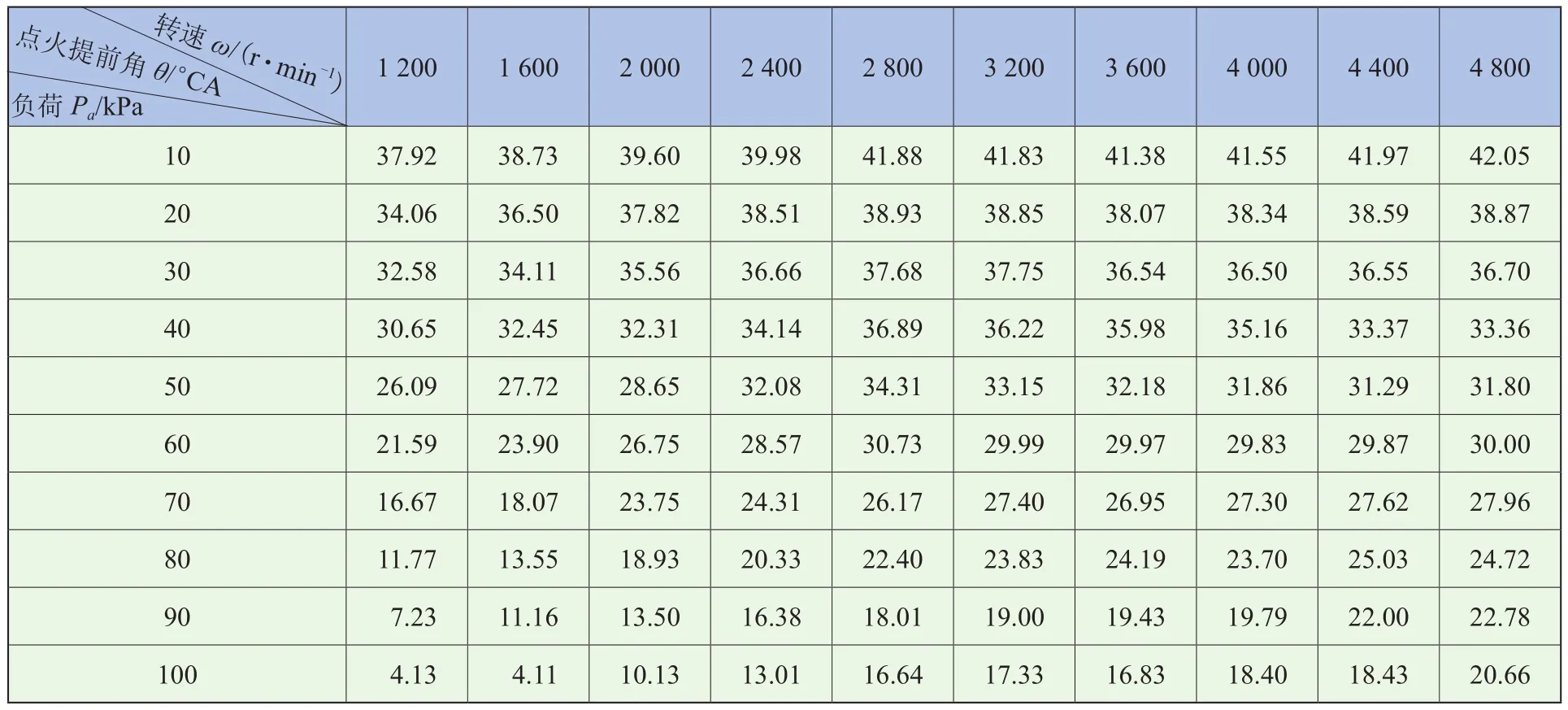
表2 不同负荷不同转速下的点火提前角
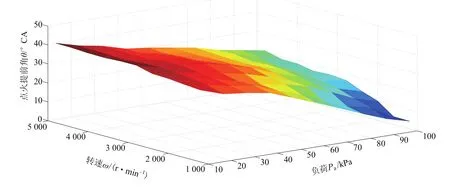
图3 试验标定点火提前角MAP图
据上述方法和理论,利用混沌RBF神经网络对点火提前角进行预测。混沌RBF神经网络模型的层数选为3层,输入层为2,隐含层为12,输出层为1。利用BP神经网络进行预测,选择隐含层个数为2。将转速1 600 r/min、2 800 r/min和4 000 r/min和不同负荷作为BP神经网络的输入,点火提前角的预测值作为输出。表3为混沌RBF神经网络预测值表,表4为BP神经网络预测值表。转速为 1 600 r/min、2 800 r/min和4 000 r/min时,根据其它工况下的试验结果,以不同的负荷为未知条件,利用样条插值法计算出点火提前角,见表5。
因此,根据混沌RBF神经网络、BP神经网络预测值和传统插值法所得值的误差(表6)可知,对于混沌RBF神经网络预测的点火提前角,与试验标定值相比,30个测试样本中均方根误差为0.090 1,平均绝对误差为0.079 0。由图4可知,混沌RBF神经网络点火提前角绝对误差分布相对均匀,且均大大低于BP神经网络预测和传统插值法所得值的误差,更加逼近试验标定值,具有更强的预测能力。

表3 混沌RBF神经网络预测值

表4 BP神经网络预测值

表5 插值法所得点火提前角
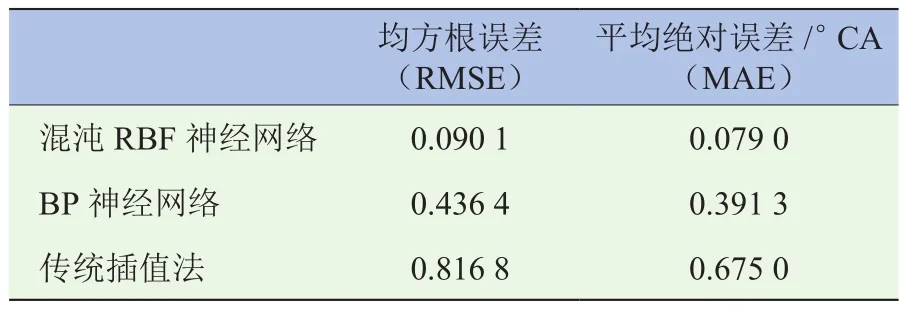
表6 混沌RBF、BP神经网络预测值和传统插值法所得值误差表
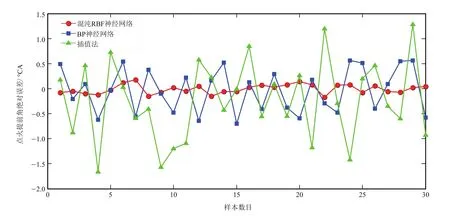
图4 点火提前角绝对误差
4 结论
(1)利用EA113发动机台架对点火提前角进行标定试验,获取了以发动机转速和负荷为影响因素的点火提前角MAP图,根据台架标定试验所得的点火提前角样本数据进行训练和仿真。
(2)运用混沌算法来优化RBF神经网络,加快其收敛速度,达到全局最优的目的,优化RBF神经网络的结构和参数,建立基于混沌RBF神经网络的点火提前角预测模型。
(3)研究结果表明,在预测汽油机点火提前角的问题上,混沌RBF神经网络模型相较于BP神经网络模型和传统插值法,预测精度得到了明显提升,具有较好的实用性和可靠性。
