六自由度道路模拟试验台架控制策略对迭代结果影响的研究

李 伟， 杨 光， 许晟杰

(中国汽车技术研究中心有限公司 汽车工程研究院， 天津 300300)

汽车行业正经历着高速发展，如何能够快速准确地验证新车型的结构疲劳强度是车企急需解决的问题。整车疲劳耐久验证方法主要包括试验场耐久试验、公共道路耐久试验和试验室台架耐久试验。对于前两种方法，气候和现实环境都会影响结果的有效性与准确性，给分析人员带来很大的干扰。而且，受各种因素影响，前两种方法还会导致整车研发周期变长。试验室台架耐久试验则可以避免外部环境的影响，在获得准确结果的同时还大大缩短整车开发周期[1-6]。

目前，在试验室进行道路模拟试验时，国际上普遍采用美国MTS公司推出的RPC(远程参数控制)技术与设备。该系统主要包括计算机、控制系统、传感器和作动器，利用RPC技术，经过数次迭代，在试验台上再现不同路面特征的激励信号。利用载荷谱进行迭代的核心是求取系统频响函数的质量，它关系到后续迭代精度，而不同的控制策略获得的系统频响函数质量不同。本文主要比较两种不同控制策略对迭代结果的影响，时域和频域结果显示迭代结果均满足后续耐久试验要求，但不同通道迭代精度依赖于控制策略的选取。

1 数据采集

在某试验场的搓板路、石块路、鱼鳞坑、扭曲路、长波路等特征路面上采集数据。基于道路试验规范，试验车行驶3圈，为后续数据的选取提供足够的样本数。数据采集系统共54个通道，包括轴头六分力通道(无制动力矩，20个)，轴头三向加速度通道(12个)，车身单向加速度通道(4个)，悬架位移通道(4个)和应变片通道(14个)。

获得所有路面载荷谱信号后对其进行分析、奇异点剔除、消除趋势项，保证载荷谱数据信号的真实性和完整性。由于MTS六自由度道路模拟台架工作频率范围是0.6～50 Hz，在进行台架试验之前对所有信号进行带通滤波处理。图1为搓板路左前轮轴头垂向力处理后的数据。

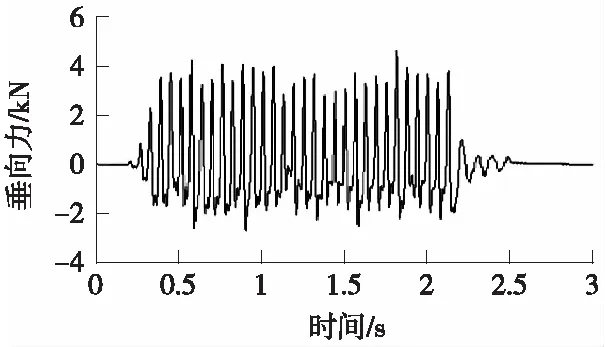
图1 搓板路左前轮轴头垂向力数据

2 系统模型识别

将试验车辆置于RPC台架上，连接所有信号线和站台机柜。建立站台配置文件，设置所有信号通道的单位、量程和极性等，确保台架试验过程中信号采集的状态与路谱采集时的状态一致。对台架的控制通道逐一进行PID调节，使台架控制系统达到最优状态。随后利用MTS提供的RPC方法，在道路模拟台架上完成对某新车型真实路面工况的复现。

2.1 远程参数控制( RPC) 的基本原理

通过设置频率信息和幅值信息，生成白噪声信号并激励系统。根据激励信号及测得的响应信号计算系统的频响函数矩阵H(f)。可以将试验台架和试验车看作一个多输入多输出的线性系统，如图2所示。

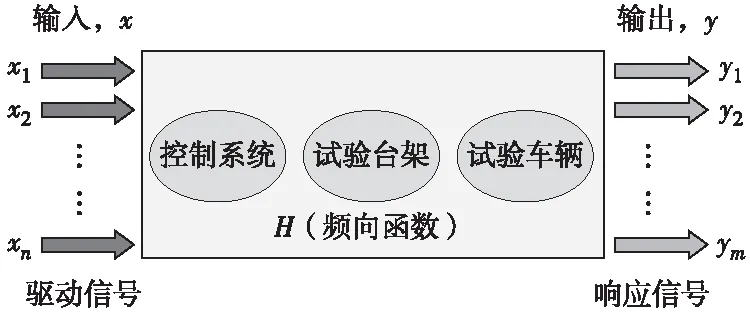
图2 多输入多输出的线性系统

频响函数的计算，实质上是一种带有误差的测试数据的估计问题。频响函数矩阵H(f)的表达式为：

Y(f)=H(f)X(f)

(1)

多输入多输出线性系统功率谱密度矩阵的线性关系式为：

Gxy(f)=H(f)Gxx(f)

(2)

通过白噪声激励信号和台架采集的响应信号可获得整个系统的频响函数H(f)，再将式(1)变形即可获得台架的驱动信号：

X(f)=H-1(f)Y(f)

(3)

由于整个试验系统的各个环节，包括试验车、控制系统等都存在非线性，使得根据线性系统计算得到的响应和目标响应之间存在较大的误差。为了消除非线性的影响，需要通过迭代逐步修正驱动信号，使系统的响应信号趋近目标信号[7-11]。迭代过程如下[12]：

1) 计算迭代首次驱动谱。

X0(f)=H-1(f)·αY(f)，x0(t)= IFFT[X0(f)]

(4)

式中：α为首次迭代设置的通道增益，一般为1。

2) 生成驱动文件。使用x0(t)激励台架和试验车构成的系统，通过数据采集系统获得系统的响应信号y0(t)，计算响应信号y0(t)与目标信号yT(t)之间的误差：

e0(t)=yT(t)-y0(t),E0(f)=IFFT[e0(t)]

(5)

进而获得驱动信号x0(t)的修正值：

ρx0(t)=IFFT[H(f)-1βE0(f)]

(6)

式中：β为迭代过程中的增益。

进而获得下一次驱动信号：

x1(t)=x0(t)+ρx0(t)

(7)

利用新的驱动信号x1(t)去激励系统，测得新的响应信号y1(t)，重复上述步骤。定义迭代指标如下：

R=ERMS/DRMS

(8)

式中：ERMS是目标信号和台架响应信号差的均方根值(RMS);DRMS是目标信号的均方根值。

2.2 两种控制策略

本次试验不涉及到制动工况，因此台架的驱动通道为20个，包括左侧纵向拉压通道，前轮侧向拉压通道等。各通道均是合成通道，各通道间存在耦合关系。路谱采集一共设置了54个通道，分别采用两种控制策略(A和B)获得两种频响函数，基于两种频响函数进行后续迭代工作。

1) 控制策略A将六分力通道作为控制通道(20个)，其他通道不参与频响函数的计算。白噪声驱动信号xi(t)为20×1的列向量，响应信号yi(t)为20×1的列向量，因此根据式(1)获得的H(f)为20×20的方阵。继而可以求得频响函数的逆函数H-1(f)。根据道路采集的目标信号yT(t)和式(4)获得台架驱动信号，据此开展迭代工作。

2) 控制策略B是将六分力通道、加速度通道、悬架位移通道和应变片通道同时作为控制通道(54个)。响应信号yi(t)为54×1的列向量，因此根据式(1)获得的H(f)为54×20的方阵。由于响应信号的个数大于台架驱动信号，因此不能依据式(3)计算台架驱动信号，式(3)需要修正，采用最小二乘法计算初始驱动信号：

X(f)= [H(f)HH(f)]-1H(f)H[Y(f)]

式中：H(f)H为频响函数矩阵的共轭转置矩阵。求取驱动信号x0(t)的修正值的式(6)需要进一步修正：

ρx0(t)=IFFT{ [H(f)HH(f)]-1H(f)HβE0(f)}

根据道路采集的目标信号yT(t)和式(7)获得台架驱动信号，据此开展迭代工作。

3 不同控制策略迭代结果对比

选取长波路、扭曲路和搓板路作为迭代路面。长波路和扭曲路是低频路面，搓板路是高频路面，通过分别迭代，能够更加全面地说明两种控制策略对迭代精度的影响。为了方便后文阐述，将长波路和扭曲路的组合路面简称为低频路面，将搓板路简称为高频路面。本次采集获得的高频路面信号，存在共振的情况，因此高频路面的迭代工作具有挑战性。

由于响应通道较多，选取损伤比重较大的六分力Fz通道(左前轮)作为观察通道。控制策略A下，低、高频路面迭代响应与目标响应信号时域、频域和统计特征值的比较结果分别见图3和图4。控制策略B下，低、高频路面迭代响应与目标响应信号时域、频域和统计特征值的比较结果分别见图5和图6。

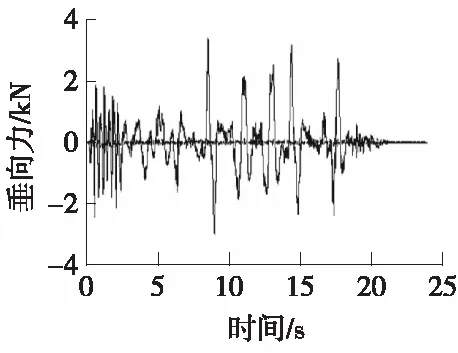
(a)时域曲线对比图

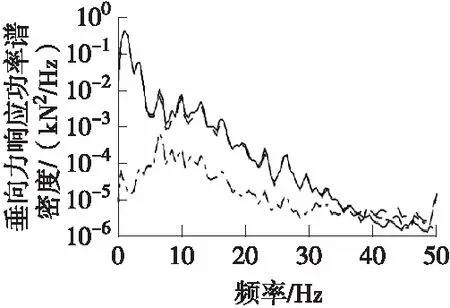
((b)频域曲线对比图

图3 控制策略A下，低频路面迭代响应与目标响应信号时域、频域和统计特征值的比较结果

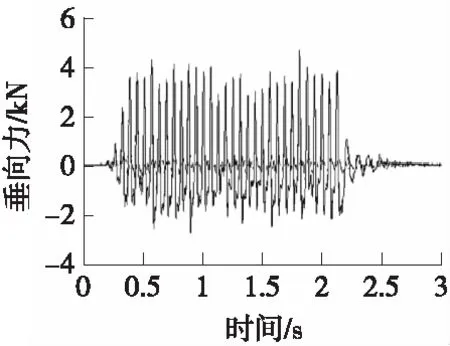
(a)时域曲线对比图

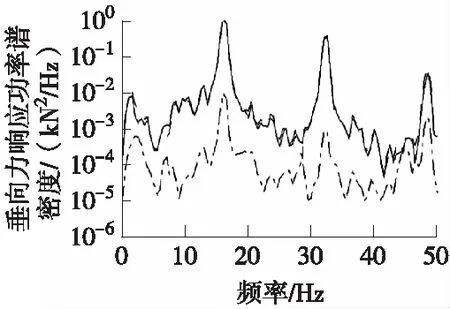
(b)频域曲线对比图

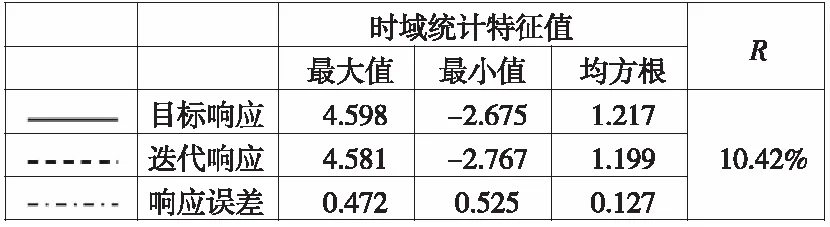
图4 控制策略A下，高频路面迭代响应与目标响应信号时域、频域和统计特征值的比较结果

(a)时域曲线对比图

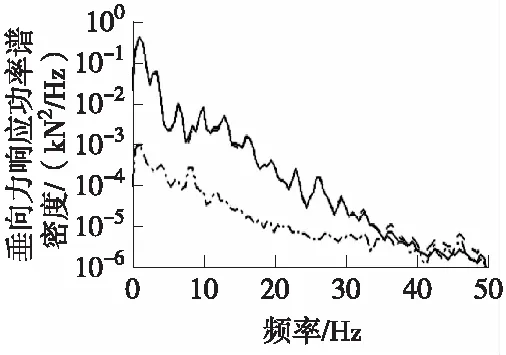
(b)频域曲线对比图

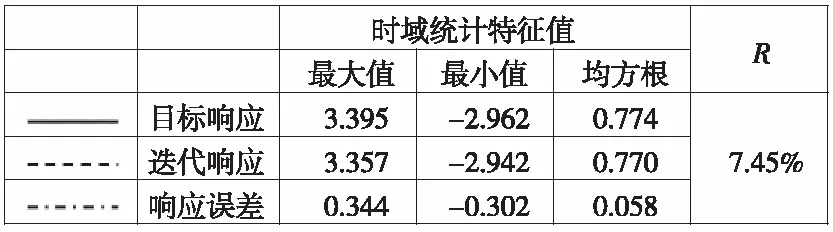
图5 控制策略B下，低频路面迭代响应与目标响应信号时域、频域和统计特征值的比较结果

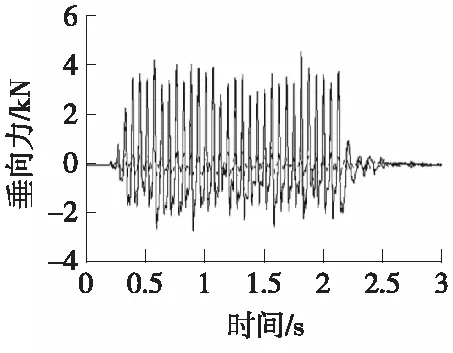
(a)时域曲线对比图

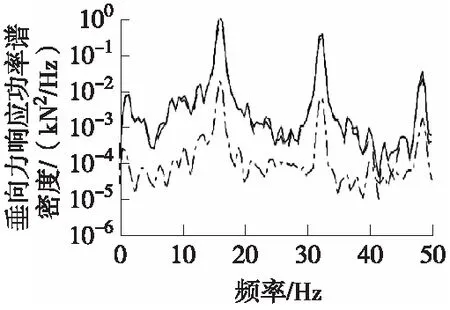
(b)频域曲线对比图

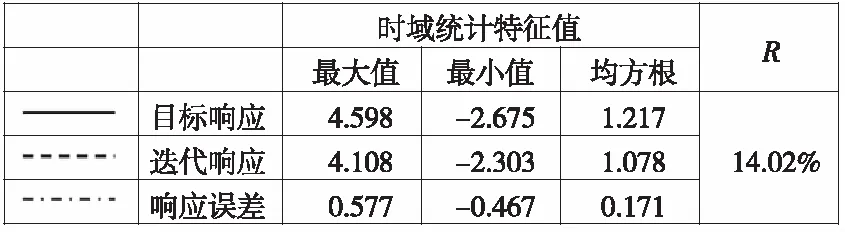
图6 控制策略B下，低频路面迭代响应与目标响应信号时域、频域和统计特征值的比较结果

从图3—图6可以看到，目标响应和迭代响应在时域和频域上几乎重合，说明台架试验能够较好地复现车辆在试车场中的受力状态，迭代精度较高。此外，两种响应的均方根值RMS非常接近，且R值均小于20%，因此六分力Fz通道在两种控制策略下的迭代结果均能满足后续耐久试验的要求。

六分力通道对台架驱动信号影响较大，尤其是每个车轮三向力(纵向、侧向、垂向)所占权重更大。为了进一步验证迭代结果，分别计算两种控制策略下，4个车轮三向力(12个通道)的R值，如图7所示。从图7中可以看到，控制策略A下三分力的R值整体上要小于控制策略B下的比值，表明在信号能量的复现方面，控制策略A要优于控制策略B。

(a)低频路面 (b)高频路面

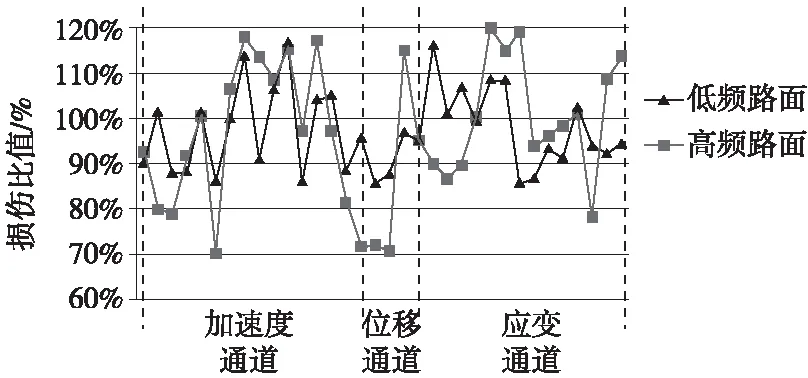
图8 迭代响应与目标响应相对损伤比值

4 结束语

对于控制策略A和控制策略B，本文获得的驱动信号都能够实现实际道路激励的复现。在获取系统频响函数时，控制通道的选取至关重要，直接影响到RPC软件求解的精度和时间。由于六分力通道与驱动信号相关性更大，因此无论如何选取控制通道，都要保证六分力的最终迭代精度。如果对除六分力以外的通道也比较关心，还可以选择其他适当的控制策略，比如可以采用六分力+加速度通道作为控制通道，采用六分力+加速度通道+悬架位移通道等作为控制通道。在进行台架试验时，控制策略的选取依赖于工程师技术水平、验证周期以及是否需要为其他部门提供数据支持等因素。本次台架试验受验证周期影响，采用策略A进行迭代，不仅缩短了迭代时间，最终台架试验结果和实际道路耐久试验结果达到了高度一致。