电感膜片对矩形波导滤波器散射参数的影响

樊琼星 刘含 黄路 蚌埠学院 电子与电气工程学院 安徽蚌埠 233000

引言

速调管的瞬时工作带宽对提高通信、雷达和电子对抗等微波电子系统的抗干扰性能十分重要。它由群聚段的带宽和输出段的带宽两部分决定，而展宽输出段的带宽是实现宽带速调管的关键。输出段的作用是保证速调管产生的高功率微波通过，传输到天线等负载。改善其带宽的主要方法是在输出传输线中设计滤波器结构。

常用的大功率宽带速调管滤波器结构通常采用矩形金属波导作为传输线，因其具有传输损耗小，功率容量大，工作频带窄和工作频率高等优点。并在波导中放置横向电感膜片作为滤波电抗元件以改善传输带宽。

本文利用微波等效电路理论，将内置膜片的矩形波导滤波器等效成微波二端口网络，计算得到二端口网络的转移参量。根据网络参量间的转换关系式，得到反映传输特性的散射参数S21的计算式。并对其进行编程计算，可以得到电感膜片的大小和放置位置对散射参数的影响。

1 等效电路理论分析法

为了保证能量均匀传输，本文选择在波导的对称位置插入大小相等的膜片。其结构如图1所示。其中l为两组膜片的间距，d为两膜片之间的窗口宽度，a和b分别为矩形波导横截面的宽边与窄边尺寸。

图1 矩形波导电感膜片滤波器示意图

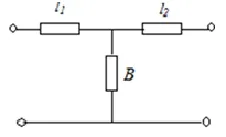
图2 图1的等效电路

由微波等效理论可知，在微波传输系统中插入一系列不均匀区，适当选取参考面后，其等效电路就是一串首尾相连的二端口网络。常取的参考面是距离为λg/2整数倍的远区。图1模型的等效电路可以看作是两段长度分别为l1和l2的均匀传输线与电纳的级联，如图2所示。它的归一化转移矩阵为：

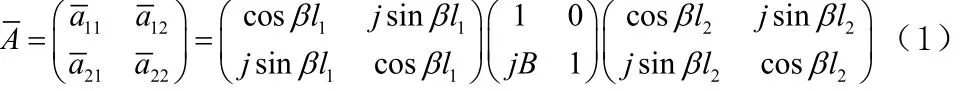
计算可得：

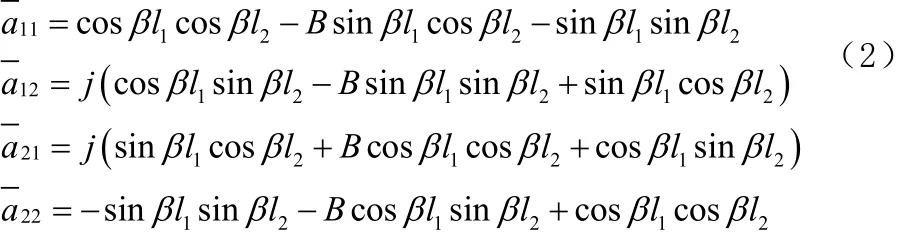
A参量和S参量都可以描述二端口网络的特性，彼此之间可以相互换算。由二者的换算得到S21：

代入式（2）整理可得：

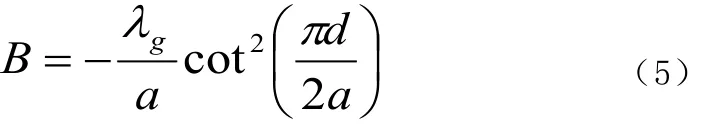
2 Matlab编程计算S21

本文矩形波导滤波器工作频率取f = 9.80GHz，波导横截面尺寸为20mm×8.3mm，横向电感膜片厚度t =1.5mm，波言编程计算了散射参数S21随波导长度l和窗口宽度d的变化关系。

(1)在窗口宽度d=6mm时，用Matlab编程计算散射参数S21随波导长度的变化。

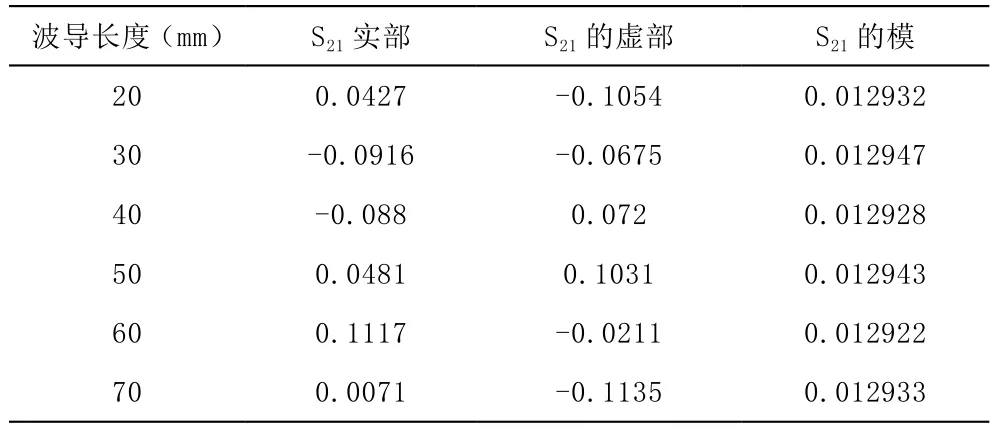
表1 Matlab计算的S21的数值

由表1可知：波导长度从20mm增大到70mm时，S21的模值不变，相位变化。

(2) 在d和l取定值，f从9.5GHz增大到10.1GHz时，S21的模随f的增大而增大。图3是d取不同值时S21的模随f的变化关系。

图3 d取不同值时S21的模随频率变化图

3 S21的仿真分析

三维电磁场仿真软件HFSS可以计算散射参量S[8。选择激励端口后，一次仿真就可以得到该端口对其他所有端口的耦合。对于无耗二端口网络结构，S参量具有对称性，整个S参量可以由一个端口得到。文中研究的模型，激励端口的设置如图4。

图4 端口的设置

(1)l取定值时，S21随窗口宽度d变化关系

根据波导横截面尺寸和内置膜片的尺寸建立模型，在l=60mm的情况下，改变窗口宽度d的大小，得出图5和图6：

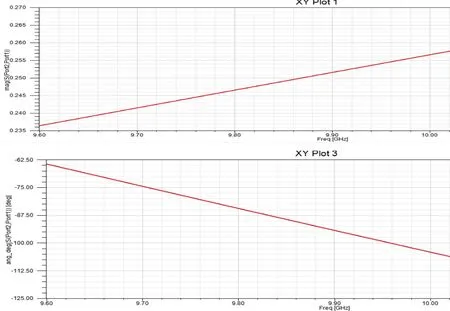
图5 d=8mmS21模值和相位随频率变化的曲线

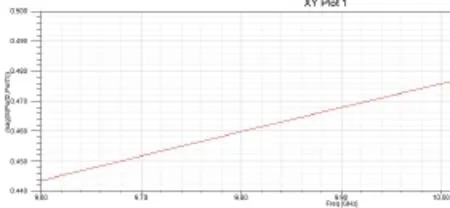
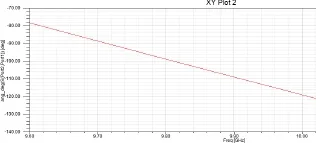
图6 d=10mmS21模值和相位随频率变化的曲线

由图5和6可知：在波导长度一定的情况下，随着窗口宽度d的变化，S21的模值和相位都变化。

(1)d取定值时，S21随波导长度l变化关系

在d=12mm的情况下，改变波导长度l的大小，得出图7和图8：

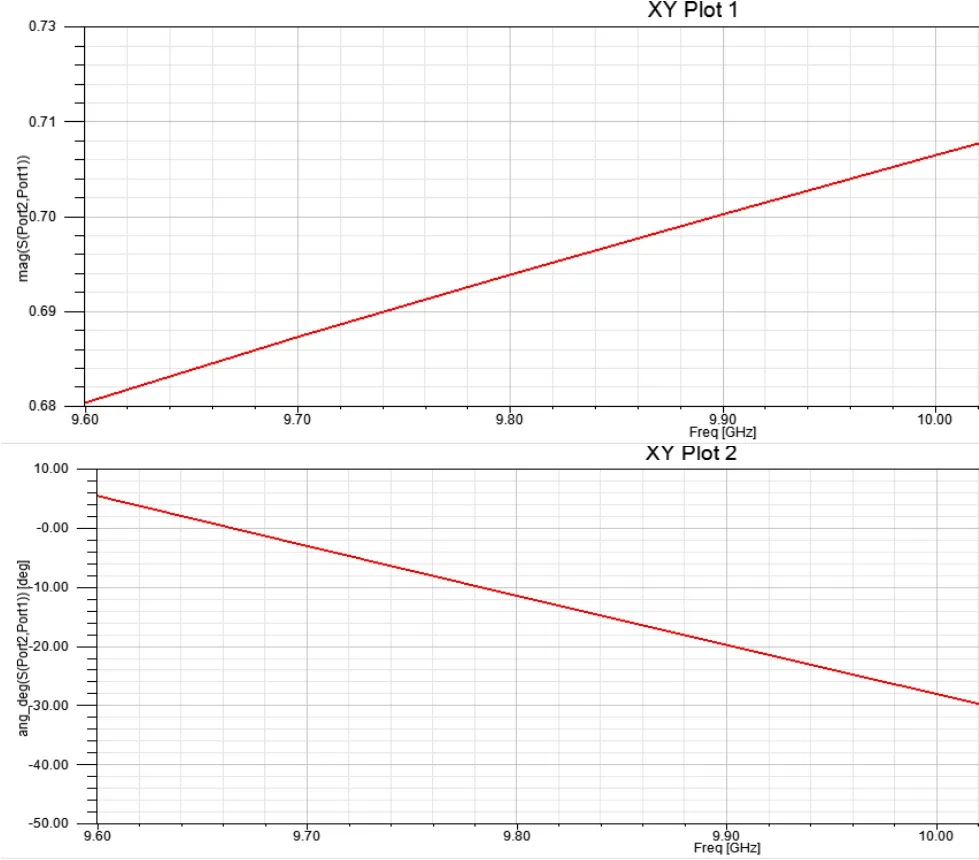
图7 l=48mm S21模值和相位随频率变化的曲线

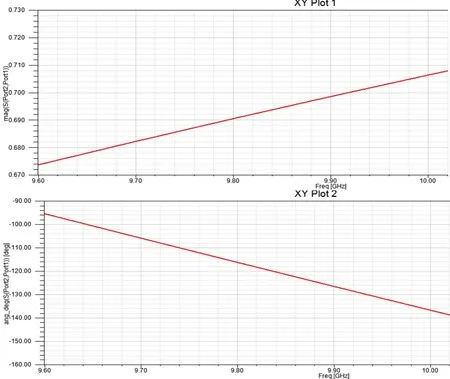
图8 l=60mm S21模值和相位随频率变化的曲线

对比图7和图8：在窗口宽度一定的情况下，改变波导长度，散射参数S21的模值不变但相位变化。即膜片两边波导的长度选取对S21幅度没有什么影响，只会影响其相位。这些仿真分析结果与理论计算结果相符。

结论

运用微波等效电路的近似方法，分析了电感膜片的大小和放置位置对散射参数S21的影响。由HFSS仿真分析得到波导长度的变化不会影响散射参数S21的模值，但波导部分长度的变化会引起入射波相位的改变，所以S21的相位会发生变化。而窗口宽度的变化会使散射参数的模值和相位发生改变。软件仿真分析的结果与等效电路理论计算结果基本一致。本文的研究结果对高频、高功率微波真空器件所用矩形波导的设计具有一定的参考意义。

在X波段内，圆弧膜片的电纳比相等面积的直膜片的电纳小的多，其电纳随频率的变化也比直膜片小的多[9]。相对于电感直膜片，圆弧膜片比直膜片更容易实现宽频带。后续会在本文的研究基础上分析圆弧膜片的位置和大小对滤波器带宽的影响。