浅谈高中数学中的不等式问题
2018-10-22欧阳昱焘长沙市长郡滨江中学
欧阳昱焘 长沙市长郡滨江中学
一、不等式在高中数学学习中的重要地位
在高中数学理论体系中,不等式是数学基础理论的重要组成部分,而不等式问题则贯穿了整个高中数学学习,例如,不等式可以应用在函数问题、三角函数问题、几何问题、平面向量问题、数列问题等,不等式问题的考查也集中在上述几个方面的问题。不等式问题的分析和解答集抽象性、复杂性、逻辑性为一体,是高中数学学习过程中较难掌握、较为棘手的问题,通常也出现在高考数学的压轴题当中。同时,在针对不等式问题分析和学习的过程中,同学们不仅可以熟悉不等式问题的基本概念,而且还能培养自身数形结合、函数与方程等思想,养成独立思考的自主学习习惯和能力。因此,熟练掌握高中数学各种类型的不等式问题的解法,不仅能够提高高考数学成绩,还能够锻炼同学们的动手计算能力和逻辑思考能力,意义重大。
二、高中数学不等式问题的类型与其对应的解法探索
纵观近十年的全国各个省份的高考数学题目,不难发现,不等式问题往往很少单独命题,出题人常常将不等式问题与其他知识点(如:函数求导、解析几何、数列等问题)相结合,以不等式为解题工具来求定义域、函数单调性、未知数的取值范围、函数极值问题函数最值问题等内容。因此,高中数学不等式问题的出题方式和考查内容主要为一下两个方面:一是直接考场不等式的相关内容,考查方式较为直接;二是引导学生以不等式作为工具,对其他重要知识点进行考查,这也是高考数学的重要考点。下面本文将列举不同类型的不等式问题并进行解法探索。
1.不等式的性质判断与应用
高中数学不等式的基本性质主要有:(1)对称性;(2)传递性;(3)乘法单调性;(4)加法单调性;(5)同向不等式可加性;(6)同向正值不等式可乘性;(7)正值不等式可乘方;(8)正值不等式可开方;(9)倒数法则。考查的重要不等式主要有:(1)基本不等式;(2)柯西不等式;(3)绝对值不等式;(4)排序不等式;(5)贝努力利等式等。高考命题人往往将不等式的基本性质和重要不等式与其他主干知识点相结合进行交汇考查。
例题1:下面四个条件中,使 ba> 成立的充分而不必要的条件是( ).
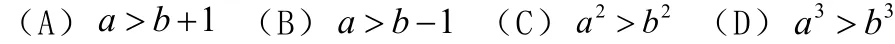
分析:此题出自2011年全国卷,主要考查不等式充要条件的判断,在解题过程中还要运用好同向不等式可加性和正值不等式可乘方等不等式的性质,通过逐项验证可解的答案为(A)。
例题2:若0>>ba,0<<dc,则一定有( ).
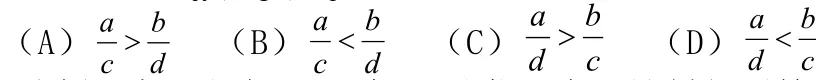

例题3:将离心率为 1e的双曲线C的是半轴长a和虚半轴长b(ba≠)同时增加)0(>mm个单位长度,得到离心率为 2e 的双曲线C ,则( )
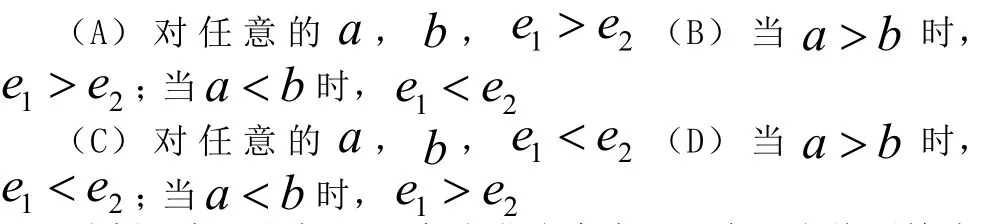
分析:此题出自2015年湖北省高考题。命题人将不等式的基本性质与圆锥曲线相结合,要想解答这道题,答题者不仅要理解不等式的基本性质和圆锥曲线的基本性质,还要将两个不同的知识点相联系,是一道典型的不等式问题。

(由解题过程可知,尽管这道高考题看起来非常抽象,同时将圆锥曲线与不等式问题相结合,增加了解题的复杂性,但是如果在审题和分析时明确命题人的出题思路,将两个看似不相关的考点合理的联系起来,解题难度就会大大下降。)
2.不等式的证明问题
在高考数学中,不等式的证明常常作为压轴题出现,可见对学生的逻辑思考能力和判断分析能力是个有效的考查。这就要求学生在解题过程中要学会通过条件分析问题,通过问题与条件的关系推导出两者之间的桥梁,进而进一步求解。

(此题出自2011年安徽省高考题,是证明绝对值不等式问题,考纲要求学生要会用比较法、分析法、综合法等证明绝对值不等式。)
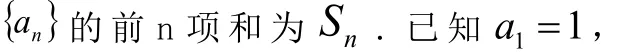

证明:①②的解题过程略。
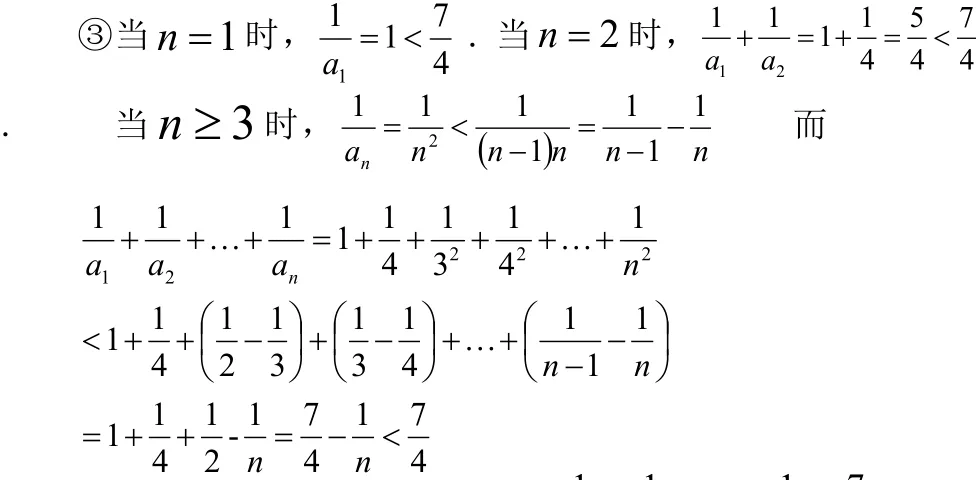
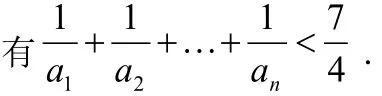

三、总结
总之,通过以上几个例题可以看出,考题的形式和内容,以及知识点的考查方式都千变万化,近年来不少创新题涌现,不同类型的知识点之间往往会相结合进行出题。但是,俗话说“万变不离其宗”,所谓的“宗”,在高中数学就是指解题过程中的数学思想,虽说命题人出题形式变化莫测难以捉摸,但是其考查的数学思想确实亘古不变的,学生在高中数学学习过程中培养一个好的数学思想方法,有利于领悟题目所蕴含的数学思想,进而提高解题效率,得出分析问题的处理方法。
