“学案导学”在高中数学复习课中的应用探讨

徐志平

摘要：“学案导学”教学模式强调学生在数学课堂教学过程中的主体作用，鼓励高中生开展整合式的自主学习，促进与同学进行合作探究，提倡学生从自己的学习意愿和学习兴趣出发对数学知识进行学习，对于提高学生的数学知识学习能力和学习效果具有非常积极的促进作用。

关键词：学案导学；高中数学；复习

中图分类号：G424

文献标识码：A

文章编号：1672 -1578（ 2018） 02 -0219 - 01

为了提升高中数学复习的阶段性效果，为了更好地提高高中生的数学知识理解能力和应用能力，为了让数学成为高中生们在未来的求学道路上的敲门砖，学者们研究了非常多有助于促进高中数学复习效果的教学方法。近年来，“学案导学”教学模式逐渐得到高中数学师的认可，越来越多以“学案导学”为主题的教学模式的创新研究如雨后春笋般涌现出来，以“学案导学”为主题的高中数学教学改革研究逐渐成为当前阶段的热点课题。“学案论和经典教育理论为基础创设的先进的数学教育模式。该模式强调学生在数学课堂教学过程中的主体作用，鼓励高中生开展整合式的白主学习，与同学进行合作探究，提倡学生从自己的学习意愿和学习兴趣出发对数学知识进行学习，教师则在整个学生自主学习的过程中扮演好“导师”的角色，以“引导”替代“驱赶”，创造高中数学教学的新模式。

1.“学案导学式”

“学案导学式”，字面解读应该是：“学案”就是教师课堂教学的主要道具，是学生在课上的学习方略，有别于由书本知识和课本习题的简单堆积的形式；“导”就是指导、引导；“学”就是自主学习。让老师从以往的知识传输、问题灌输的教学，转型为学生的自我“能动学习”。在课堂上，师生的对话与合作、碰撞与研究，生成形成智慧的足迹。“学案导学式”是把学生现有的认知水平、知识基础，作为教师编制学习目标、学习重难点、学习模块的设计方案从而达到学生主动学习的效果。通过这种形式把教师的教与学生的学二者之间有机的构建了一座桥梁，教师的任务就是在课堂上辅助学生自主掌握课堂内容的前提下，培养他们独立学习的习惯和自主搭建知识体系的能力，这是学生学习的总方针。

2.复习课“导学案”的设计原则

在高中数学的复习课中，“导学案”是应用学案导学教学模式的关键。为了最大限度地保证复习课的教学质量，教师在设计高中数学复习课的“导学案”时应当注意遵循以下原则：

2.1 以学生为主体的原则

复习课的主要内容就是让学生将自已已经学过的知识点串联起来，将原本孤立存在的数学知识融合转化为学生们解决数学问题的数学思维能力、数学问题解决能力。所以，复习课的“主角”是学生。针对复习课设计的“导学案”应当充分尊重学生在复习过程中的主体作用，将课堂复习教学工作的组织和开展都紧密围绕着高中生数学能力的培养需要来展开。

2.2 保持课程的探究性原则

对于复习课来说，由于没有新知识的学习压力，所以教师在以往的教学过程中也并不太重视对课程内容探究性的保持。但事实上，保持一定的探究性，能够有效引发学生的自主思考，反而有助于复习效果的达成，所以，在编写高中数学复习的“导学案”的过程中教师应当注重对教学内容和教学环节的设置，保持课堂的探究性特色。

2.3 构建阶梯目标体系原则

从高中数学复习课的特点出发，复习课就是要将所有已经学过的高中数学知识点进行串联。所以，在编写复习课的导学案的时候也应当注意知识点难度的递进性。以高中阶段出现的所有与“不等式”有关的知识点为例。在对高中数学不等式的相关知识点进行复习的时候，教师可以知识点之问的相互关系，由简到难，设置四个阶层的学习目标体系，第一阶层的目标为学生能够用白己设计的数学题来准确地描述“不等式”的定義。第二个阶层的目标为学生能够用白己设计的数学题来准确地描述“不等式的性质”、“一元二次不等式”、“简单的线性规则”。以此类推，随着数学知识点难度的提升，学生的数学知识转化应用能力也在不断地增强。

2.4 坚持知识内容专题化原则

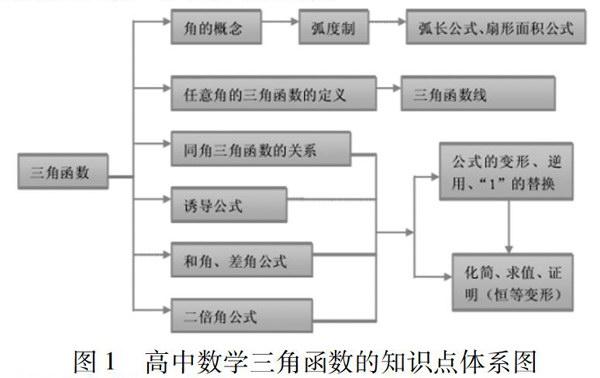
事实上，高中数学知识点之问的关联性是非常强的，比如“三角函数”和“三角函数的图象”和“平面向量”和“解三角形”这四个单元的知识点之问就有着千丝万缕的联系，但是这四个单元的知识点又自成体系，所以，在进行复习课“导学案”设计的时候，既可以将“三角函数”、“三角函数的图象”、“平面向量”和“解三角形”这四个单元作为独立的一个主题进行“导学案”的设计（如图1示），也可以以“三角函数与平面向量”为一个大的主题进行“导学案”的设计。

3.高中数学复习课“学案导学”的课堂片段实录

片断1：“案例分析”环节学生释惑解疑

生1：老师，函数f（x）=X2 _4满足f（-x）=f（x），所以函数f（x）为偶函数，我的解答过程哪里做错了？

生2：这个题目中f（x）的定义域为X∈[ -1，2]，不关于原点对称，所以，（x）的奇偶性是非奇非偶。

生1：如果题目中函数自变量的范围改为X∈[ -1，1]，那我这种方法就对了。

师：同学们来评判一下，生1的说法是否有道理？

生3：如果题目中函数自变量的范围改为X∈[ -1，1]，生1的方法就对了。

生4：我不认同，生1从f（-1）=f（l）得出f（-x）=f（x）从而得到f（x）在定义域上是偶函数的结论，而根据必修1书上第33页奇偶性的定义，必须对定义域内的任意一个x都成立才可以。

师：生4讲的很好，定义域内只有部分x满足f（-x）=f（x）不能推出函数f（x）在定义域上是偶函数的结论，必须对定义域内的任意一个x都成立才可以。值得注意的是函数具备奇偶性的前提是其定义域要关于原点对称。

生1：老师我懂了。

上述的一幕幕在我们的复习课堂中经常出现，这里面蕴涵了学生的智慧，完美的呈现了学生的概括能力、思辨能力和表达能力，从课堂中我们看到了学生对复习课堂自主驾御的渴望和满足感，它带来的积极效果可想而知了，而这正是我们的有效教学的课堂所迫切需要的。

参考文献：

[1] 孙小明，“高中数学学案导学法”课堂教学模式的构建与实践[J].数学通讯.2015.

[2] 桂杰，“学案导学”模式在中学数学教学中的应用研究[D].山东师范大学.2013.