基于因子分析的高等教育综合水平研究

崔婉婉

摘要：以2015年中国31个省高等教育综合水平的七项指标为依托，采用因子分析法对31省的高等教育水平进行综合评价，得出了符合实际情况的因子得分综合排名。结果表明：因子分析法全面考虑了影响高等教育的各项指标，不仅解决了各项指标之间的相关重叠性，还客观确定了各项指标权重，最终的综合评价结果符合中国高等教育的实际情况。

关键词：高等教育；因子分析；SPSS

0 引言

在新时期社会对高综合素养与高专业技能水平的人才需求水平越来越高，深化教育事业改革已经深入到我国教育事业的各个阶段和各个方面。综合评价是在高等院校教学工作中的一个重要环节，他可以避免教学活动偏离目标，保障教学质量，使教育的社会效益和经济效益最大化。因此探讨出一种有目的、有计划的评价方法，为提高教学质量、提升教育价值提供定量化的参考和依据成为各方关注的焦点。

1数据来源和研究方法

根据2015年中国国家统计局官方数据，以我国31个省份作为样本，7项指标进行评价，该7项指标的具体含义为：x1普通高等学校数量（所）、 x2教育经费（万元）、x3普通高等学校在校学生数（万人）、x4普通高等学校教职工总数（万人）、x5普通高校生师比（教师人数=1）、x6每十万人口高等学校平均在校生数（人）、x7特殊教育学校数（所）。

本文采用基于因子分析的多指标综合评价法。

2 因子分析过程

2.1 数据处理过程

利用SPSS19.0软件进行因子分析，为了消除原始数据数量级与量纲的差异，首先将数据标准化处理；其次建立相关系数矩阵。

本文通过检验和的球形度检验看数据是否适合做因子分析，其中，球形度检验近似卡方为248.180，自由度为21，趋近于0.000<0.05，这个结果表明相关系数矩阵不是单位阵，所选取的变量之间存在相关性。用于检验变量间的偏相关性，度量值越接近于1，說变量之间的偏相关性越强，因子分析的效果越好。度量值为0.789，由此可知选取的变量适合做因子分析。

运用SPSS计算得出的个指标相关矩阵特征值和方差累计贡献率，前两个因子的累计方差贡献率达到了83.594%，说明前两个因子反映了原始变量83.594%的信息；根据特征根大于1，累计方差贡献率大于85%的原则，我们可以近似认为前两个因子具有显著性，符合进一步进行分析的要求。

公共因子与指标之间的关联关系程度由因子负荷矩阵来体现，采用最大方差法进行因子旋转，得到旋转前后的因子负荷矩阵和各因子得分系数矩阵。

由旋转因子负荷矩阵可知，指标按正交负荷的高负荷量分为两类，对各个主子进行分析，各主因子命名为：F1基础教育资源因子（X1普通高等学校数量、X2教育经费、X3普通高等学校在校学生数、X4普通高等学校教职工总数、X7特殊教育学校数）；F2高等教育规模因子（X6每十万人口高等学校平均在校生数）。

2.2 因子综合得分及评价

利用因子得分系数矩阵，可得各成分因子的得分如下：

将各省标准化后的各项指标数据代入上式，求出基础教育资源因子、高等教育规模因子得分，然后以各因子方差贡献率占两个因子总方差贡献率的比重为权重进行加权求和，可得每个省的综合因子值F，即综合评价值，其表达式为：

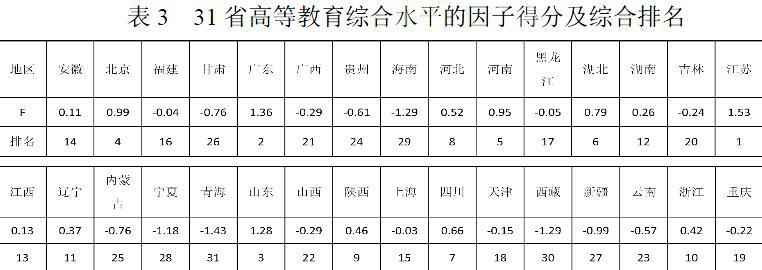
从表3我们可以看出，综合得分F的排名与基础教育资源因子的排名基本上一致，这说明一个省份的整体教育水平很大程度上取决于它的基础教育资源。

4 结论与建议

采用因子分析法对31个省的高等教育进行综合评价，共使用了反映高等教育的7项计量指标，不用关心指标间的重叠性，也不要人为主观地确定指标权重，用因子分析得出了比较确实的结果。因此，利用因子分析综合评价高等教育水平是行之有效的，其具有科学性和可操作性。

参考文献：

[1]唐林俊，杨虎.西部地区经济发展状况的因子分析[J].学术纵横，2008（5）：125.

[2]中国国家统计局.中国统计年鉴[M].北京：中国统计出版社，2015.

[3]王学民.应用多元分析[M].上海：上海财经大学出版社，1999.