基于WLS-SVM的加速度计动态模型参数辩识
2018-10-19王建林郭永奇魏青轩胡红波
王建林,郭永奇,魏青轩,孙 桥,胡红波
(1.北京化工大学 信息科学与技术学院,北京 100029;2.中国计量科学研究院,北京 100029)
在航空航天、机械电力、地质探测、汽车工业等领域广泛存在振动与冲击,加速度计作为测量振动与冲击的惯性传感器,其动态模型对研究与分析加速度计的动态特性及提高振动与冲击测试系统的动态测量精度具有重要作用。
加速度计动态校准是研究其动态模型及动态特性的重要方法,主要有正弦振动激励校准和冲击激励校准,并已建立了相应的国家基准和校准装置[1-4]。
利用加速度计的正弦振动激励校准和冲击激励校准实验数据,建立加速度计动态模型,全面表征加速度计的动态特性。加速度计动态模型参数辩识以自回归模型或频率响应函数为基础,利用参数辩识方法在时域或频域实现参数辨识。俞阿龙[5]利用遗传算法全局搜索的特点,实现了基于遗传神经网络的加速度计动态模型参数辩识,弥补了神经网络易陷入局部极值的不足,保留了神经网络局部搜索能力强的优点;杨子恺等[6]构建加速度计的线性带外生变量的自回归滑动平均模型,描述了加速度计的输入输出特性及噪声,采用预测误差法估计动态模型参数,模型输出与实测加速度计输出曲线吻合良好;以上方法直接使用加速度计输入输出数据实现参数辨识,均为加速度计动态模型参数时域辨识方法,这些方法存在参数辨识数据计算量大、模型阶次较高、易受高频噪声干扰等缺点。参数频域辨识方法具有辨识过程数据计算量小、不易受高频噪声影响等优点,已在加速度计动态模型参数辨识中得到应用。Link等[7]使用加速度计正弦振动激励校准数据,应用加权最小二乘(Weighted Least Squares,WLS)在频域辩识加速度计动态模型参数,并采用Monte Carlo方法评定了加速度计动态模型参数的不确定度;Link等[8]利用加速度计冲击激励校准数据,采用最小二乘(Least Squares,LS)方法在频域辨识加速度计动态模型参数,模型参数辨识结果与绝对法正弦振动激励校准数据辨识结果比较,具有较好的一致性,该方法被广泛应用于加速度计冲击激励校准。胡红波等[9]采用中国计量科学研究院的高g值和低g值的加速度计冲击激励校准装置,在频域应用LS方法辩识加速度计动态模型参数,取得了较好的效果。然而,加速度计动态模型参数时域或频域辩识方法都是以加速度计二阶线性模型为基础进行模型参数辨识,实际上,冲击激励加速度计校准实验数据分析表明,由于加速度计存在的非线性,仅利用二阶线性模型不能准确预测冲击加速度计的输出[10]。在加速度计动态模型参数辩识中,加速度计的非线性导致加速度计二阶线性模型参数为有偏估计[11],尤其是当加速度计的非线性较明显时,其动态模型参数辨识结果会产生较大误差。支持向量机(Support Vector Machine,SVM)是由Vapnik等提出的以结构风险最小化为准则的机器学习方法,对于小样本、非线性的建模问题具有独特的优势[12],适合用于加速度计的非线性估计。
针对加速度计存在的非线性对其动态模型参数辨识精度的影响,本文通过引入非线性项,构建加速度计二阶非线性动态模型,描述其动态特性;提出了一种基于WLS和SVM的加速度计动态模型参数辩识方法,采用WLS辨识加速度计动态模型中线性部分参数,并利用SVM估计加速度计动态模型中非线性特性,通过反复迭代,最小化频域误差准则函数,实现加速度计动态模型参数的最优辩识。
1 加速度计二阶非线性动态模型
在线性动态范围内,加速度计可以简化为一个单自由度“质量-弹簧-阻尼”系统,能够用二阶线性模型表征其动态特性,如图1所示。
弹簧和阻尼器与质量块相连固定于加速度计底座上,当加速度计随被测运动体发生运动时,质量块相对于加速度计底座发生位移,质量块的运动方程为

图1 单自由度质量-弹簧-阻尼系统Fig.1 The one degree of freedom spring-mass-damper system

(1)
式中:m为质量块质量,k为弹簧的弹性系数,c为阻尼器的阻尼系数,R(t)为质量块相对于惯性坐标系位移,S(t)为加速度计底座相对于惯性坐标系位移。
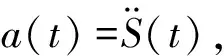
(2)
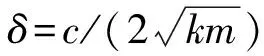
对式(2)两边同时进行拉氏变换,得到加速度计传递函数
(3)
实际上加速度计动态特性存在非线性,其动态模型本质上是非线性的,在加速度计的高精度应用场合,加速度计存在的非线性影响其动态性能。因此,为了准确地表征加速度计动态特性,不失一般性,加速度计动态模型可用二阶非线性模型描述,即在式(3)中引入非线性项Δρ(s),以表征加速度计的非线性,加速度计动态模型可以表示为
(4)
令HL和HNL分别表示加速度计动态模型的线性部分与非线性部分,加速度计动态模型为
H(s)=HL(s)+HNL(s)
(5)
2 基于WLS-SVM的加速度计动态模型参数辩识
2.1 加速度计动态模型线性部分参数辩识

(8)
设加速度计输入与输出数据分别为a(n)和x(n),对应的傅里叶变换分别为A(jω)和X(jω),则直接由加速度计的输入输出数据,经傅里叶变换得到的加速度计频率响应函数为
(9)
在加速度计冲击激励校准实验中,冲击激励信号脉宽影响其带宽,带宽外的频域数据不确定度较大,而应用LS在频域辩识加速度计动态模型参数方法中,频域数据点的权值相等,使得模型参数辨识结果不确定度较大,精度较低,激励信号带宽越小,模型参数的不确定度越大,精度越低。因此,依据信噪比确定频域数据点的权值,应用WLS估计加速度计动态模型线性部分的参数,提高动态模型参数辩识精度。
记加速度计输入与输出数据的频域信噪比分别为SNRA和SNRX,且满足
(10)
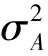
定义频域误差准则函数为
J(μ)=
(11)
2.2 加速度计动态模型非线性估计
SVM能够在高维空间构建线性拟合,解决非线性估计问题,本文采用SVM实现加速度计动态模型非线性估计。
选取加速度计频率响应函数的频率区间[ω1,ωL],令加速度计非线性的样本集为{z,y},其中
z=(Re(jω1),…,Re(jωL),Im(jω1),…,Im(jωL))
y=(Re(HNL(jω1)),…,Re(HNL(jωL)),
Im(HNL(jω1)),…,Im(HNL(jωL)))
(12)
通过非线性映射:z→φ(z)转换到高维空间,非线性拟合问题变换为线性拟合问题,即
f(z)=aT·φ(z)+b
(13)
式中,·表示内积,a的维数为高维空间的维数,b∈R为阈值。
引入松弛变量ξ,ξ≥0,根据结构风险最小化准则,拟合问题转化为如下的优化问题
(14)
其中,C为惩罚系数。
优化问题的约束条件为
(15)
式中,ε为精度,C越大表示对训练误差大于精度ε的样本的惩罚越大,ε越小,回归函数与输出的误差越小,估计精度越高。
2.3 加速度计动态模型参数辩识
在频域利用WLS实现加速度计动态模型线性部分参数辨识,利用SVM估计加速度计非线性,通过多次迭代,实现加速度计动态模型参数最优辨识。
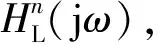
基于WLS-SVM的加速度计动态模型参数辩识算法的流程图如图2所示。

图2 基于WLS-SVM的加速度计动态模型参数辩识算法流程图Fig.2 Flow chart of parameters identification algorithm of the accelerometer dynamic model using WLS-SVM
基于WLS-SVM的加速度计动态模型参数辩识算法步骤如下:
步骤1对加速度计冲击激励校准输入与输出数据作傅里叶变换,由式(9)求得加速度计频率响应函数H1(jω);
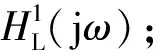


3 实验与分析
3.1 仿真实验
利用MATLAB软件仿真加速度计冲击激励校准的激励与响应信号,其中,冲击激励信号通过四阶巴特沃斯滤波器产生,截止频率为10 kHz,采样频率为10 MHz,数据长度为5×104,定义仿真加速度计动态模型线性部分HL(s)的参数分别为δ=0.006 0,ωn=2.700×105rad/s以及ρ=3.200 0×105;根据加速度计(型号:XK101S)冲击激励校准实验数据分析其存在的非线性,令仿真模型的非线性动态特性接近加速度计(型号:XK101S)的非线性动态特性,定义仿真加速度计动态模型非线性部分为
Δρ(s)=(τs)-0.9
(16)
式中,τ=0.005。仿真的加速度计冲击激励信号与响应信号时域波形如图3所示,由式(9)求取的加速度计频率响应函数如图4所示。
选取频率段0~50 kHz,应用本文提出的基于WLS-SVM的加速度计动态模型参数辩识方法,通过迭代实现加速度计动态模型参数辨识,并与文献[8]的方法进行比较,文献[8]中针对加速度计二阶线性模型,采用双线性变换得到模型的离散传递函数,进而得到频率响应函数,在频域利用LS辨识加速度计动态模型参数,所得模型参数辨识结果如表1所示。由表1可知,应用本文提出的加速度计动态模型参数辩识方法所得加速度计动态模型参数辨识结果更接近设定值,相对误差较小,相比于文献[8]的方法,本文方法克服了非线性对加速度计动态模型参数辨识结果的影响,使得δ辨识精度提高了1.67%,ρ辨识精度提高了0.12%。
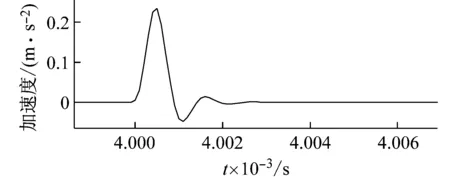
(a) 加速度计冲击激励信号
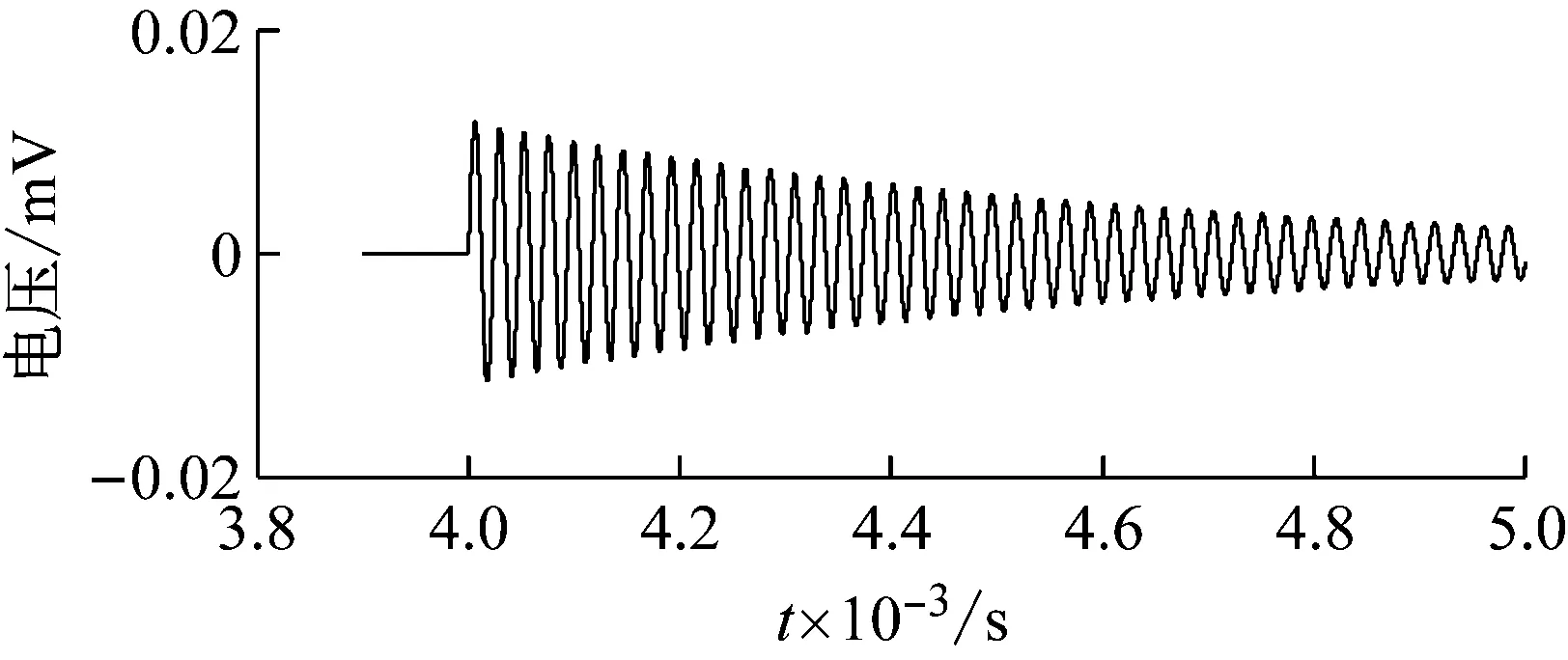
(b) 加速度计响应信号
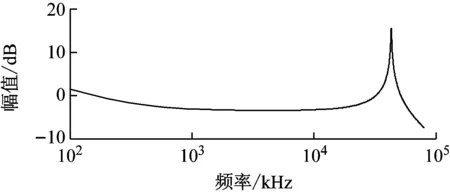
(a) 幅频响应
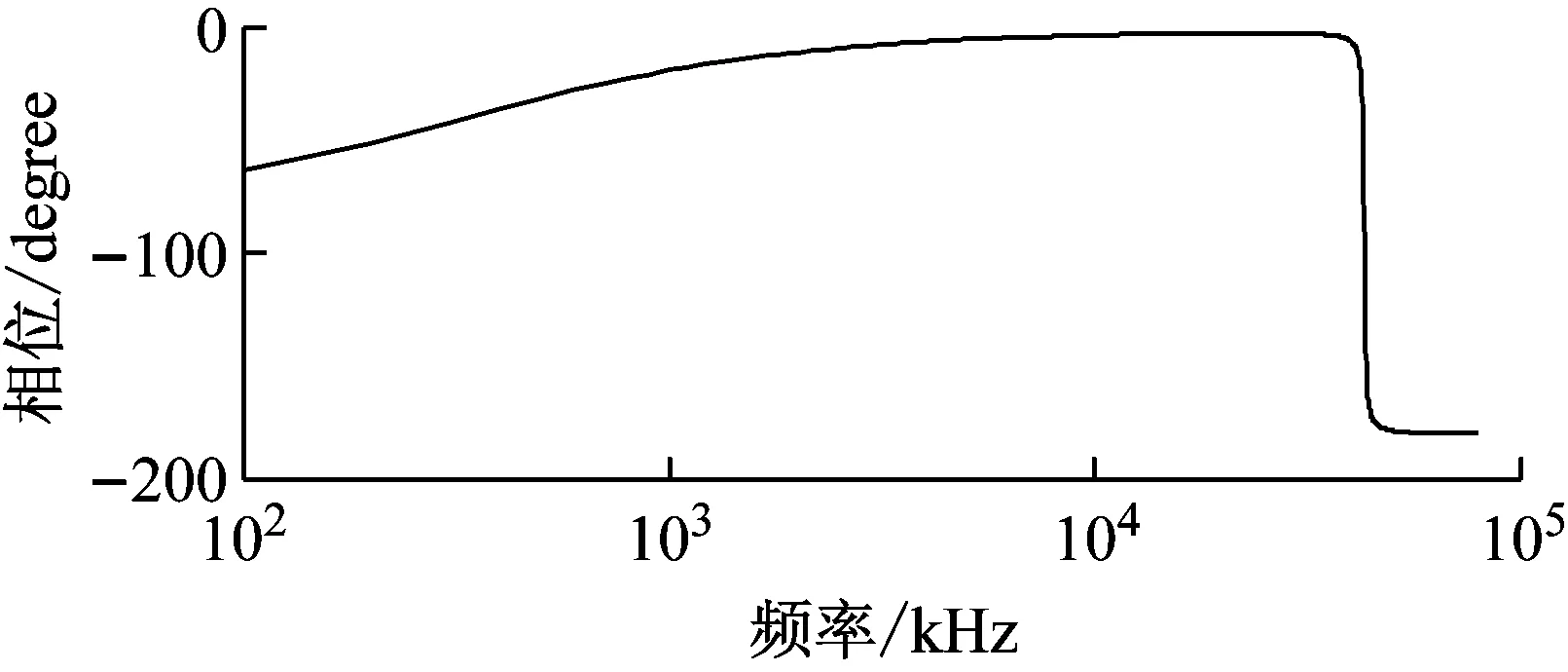
(b) 相频频响应
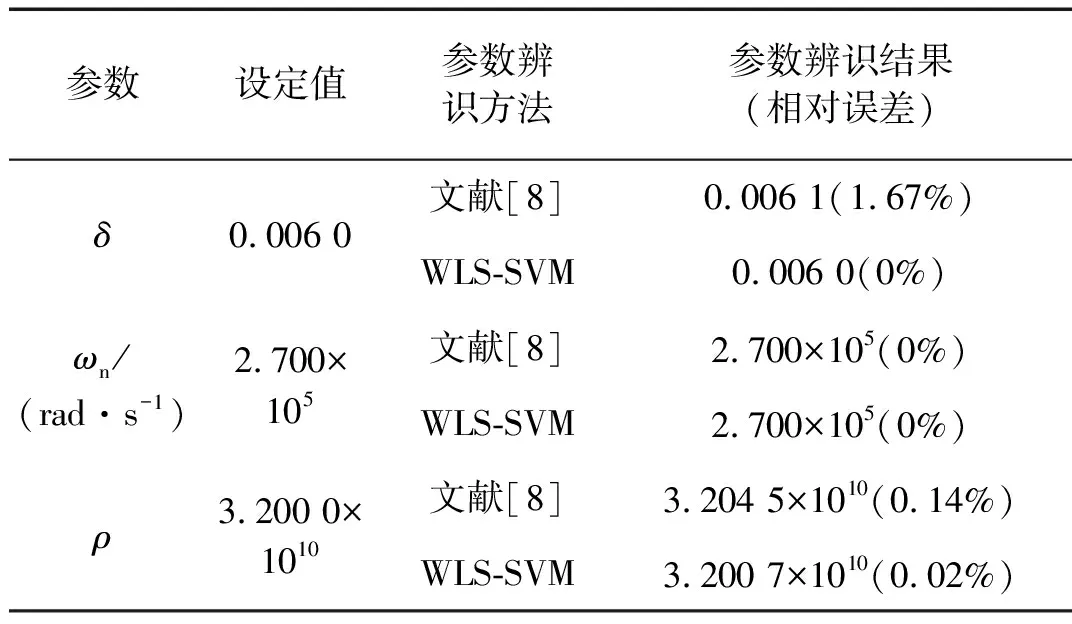
表1 仿真实验模型参数辨识结果Tab.1 Results of model parameter identification in simulation experiments
3.2 加速度计冲击激励校准实验
采用中国计量科学研究院的加速度计绝对法冲击激励校准装置获取加速度计冲击激励校准实验数据。加速度计绝对法冲击激励校准装置如图5所示。

(a) 装置结构图

(b) 实物图
该装置由高压仓、弹丸、Hopkinson杆、激光干涉仪、PXI采集板卡等组成。加速度计通过螺栓固联于Hopkinson杆的一端,当弹丸以一定速度撞击Hopkinson杆的另一端,会在此端面产生近似正弦波的应力波,应力波沿Hopkinson杆传播到另一端面,通过多次反射产生冲击加速度,利用激光干涉仪测量Hopkinson杆末端的位移信号,对位移信号作两次微分处理得到被校加速度计的冲击激励信号。加速度计的输出经过放大器转换为电压信号,PXI采集板卡对激光干涉仪输出与加速度计输出信号同步采样。
利用上述绝对法冲击激励校准装置对加速度计(型号:XK101S)进行六次绝对法冲击激励校准实验,并以100 MHz采样频率对激光干涉仪的输出信号与加速度计输出的电压信号同步采样,激光干涉仪的输出信号经过计算机解算转换为对应的加速度信号。六次校准实验中,加速度计输入输出信号前5个波峰和波谷值如表2所示,重复性良好。第一次实验采样获得的加速度计输入与输出信号时域波形如图6所示,针对加速度计输入与输出数据,由式(9)求取加速度计频率响应函数,结果如图7所示,由于受加速度计非线性影响,其幅频响应和相频响应不符合二阶线性模型的幅频响应和相频响应。
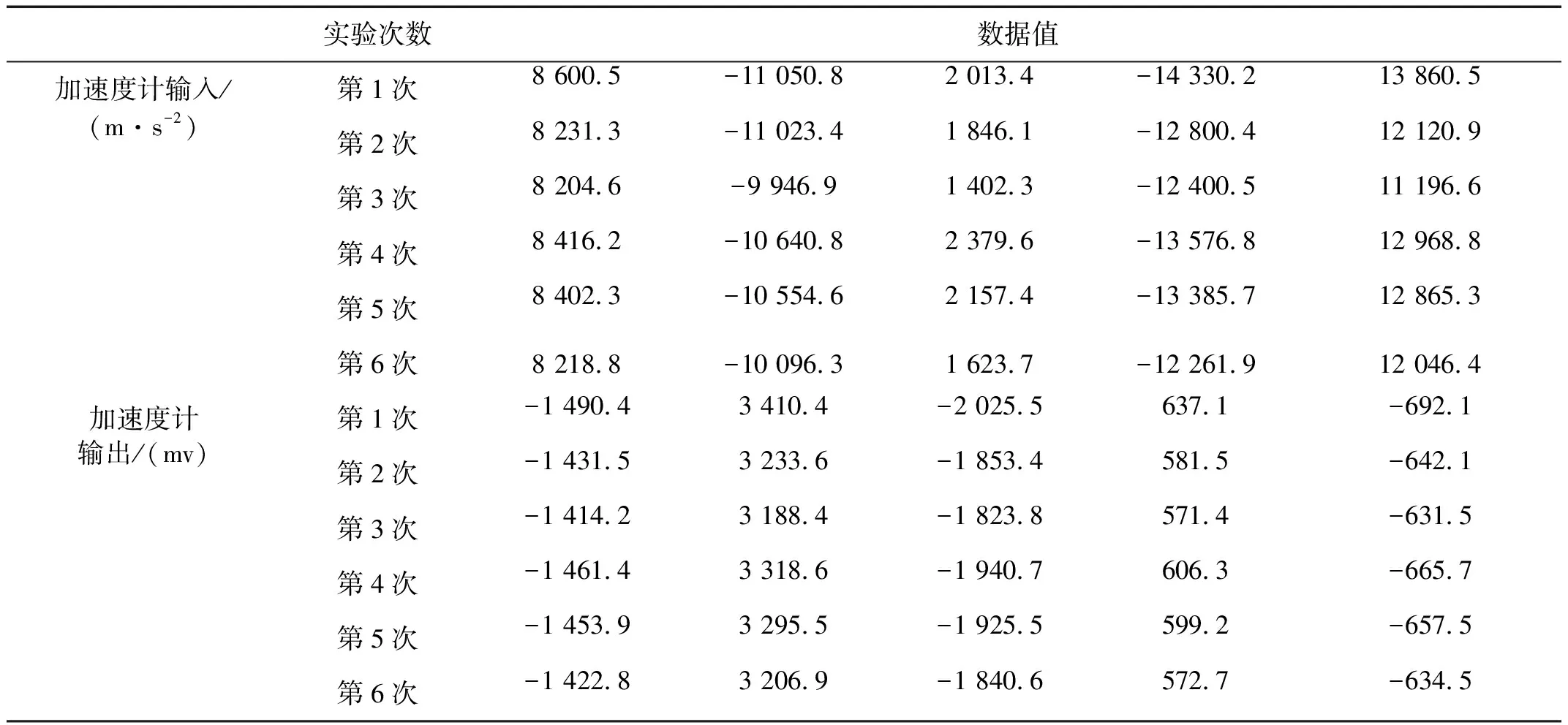
表2 加速度计输入输出信号波峰和波谷值Tab.2 Peak and trough data of accelerometer input and output signal
针对此六次实验的数据,分别应用文献[8]方法和本文提出的加速度计动态模型参数辩识方法进行加速度计动态模型参数辨识,辩识结果见表3。由表3可知,对于固有频率ωn,两种方法所得参数辨识结果较为一致,这是由于被校加速度计非线性对固有频率影响不大,而对于阻尼比δ和转换系数ρ,两种方法所得参数辨识结果虽在数量级上保持了一致,但由于受非线性的影响,利用文献[8]方法所得参数辨识结果的标准差明显偏大,而本文提出的加速度计动态模型参数辩识方法所得参数辨识结果标准差较小,具有较高的一致性,表明了基于WLS-SVM的加速度计动态模型参数辩识方法受非线性影响较小。

(a) 加速度计冲击激励信号

(b) 加速度计响应信号
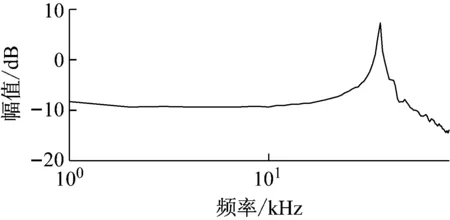
(a) 幅频响应

(b) 相频频响应
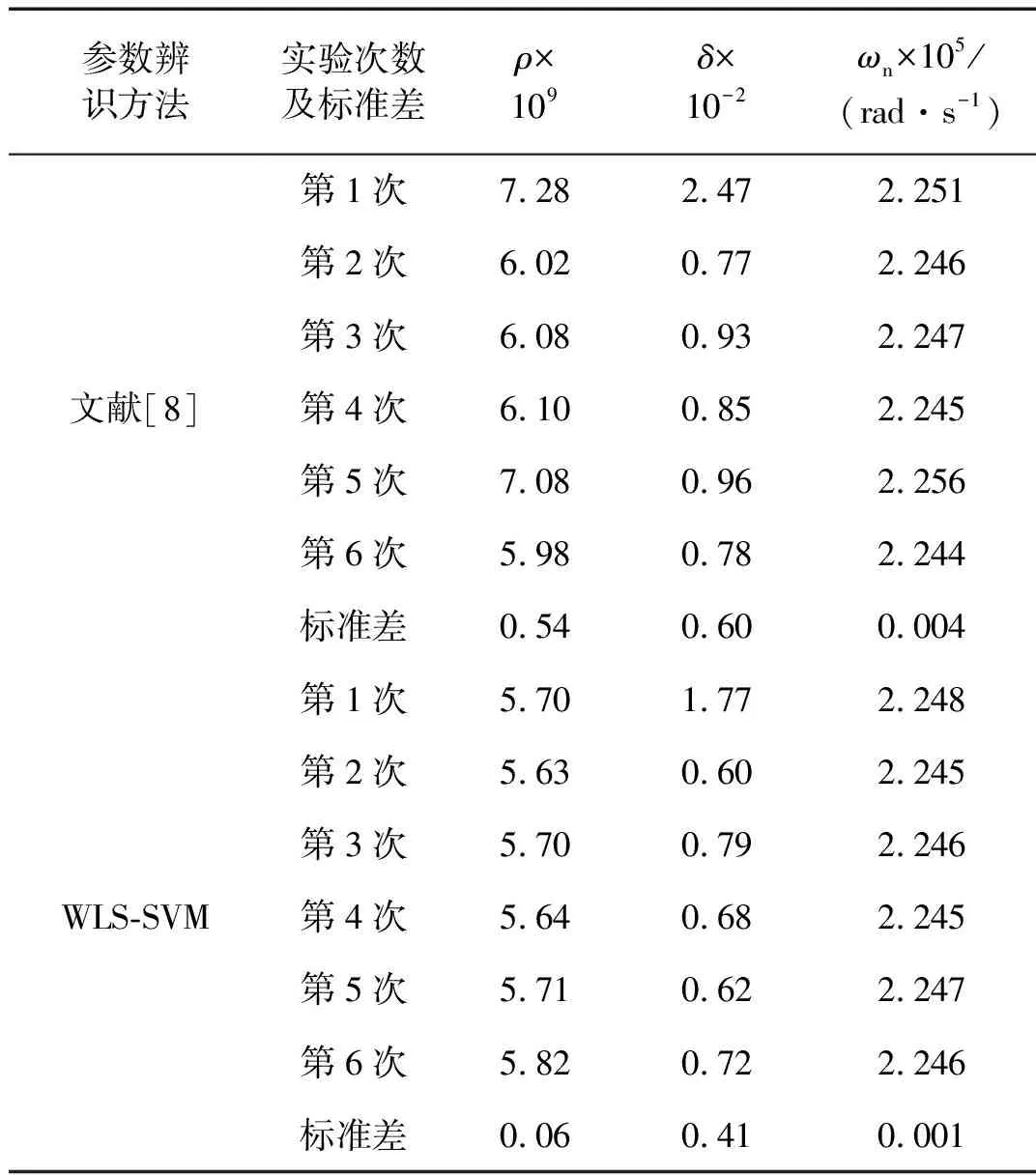
表3 校准实验模型参数辩识结果Tab.3 Model parameter of identification in calibration experiments
4 结 论
本文提出了一种基于WLS-SVM的加速度计动态模型参数辩识方法,在加速度计线性二阶动态模型基础上,为了准确地表征加速度计动态特性存在的非线性,通过引入非线性项,构建加速度计二阶非线性动态模型,描述其动态特性;分别利用WLS和SVM迭代计算,在频域实现加速度计动态模型参数辩识,有效地减小了加速度计非线性对其动态模型参数辩识精度的影响,具有较强的抗非线性干扰能力,具有较高的模型参数辨识精度。
